基于动态图的软件水印算法
2015-01-05胡若翔谭逢亮
雷 敏,杨 榆,胡若翔,谭逢亮
(1.北京邮电大学信息安全中心,北京100876;2.灾备技术国家工程实验室,北京100876)
0 引言
软件水印主要用于保护软件的版权,分为静态水印和动态水印[1-6],其中动态软件水印保存在程序的执行状态中。在动态软件水印算法中,最具代表性的是 CT[7,8]和 NT[9]算法。
研究基于已有的CT动态图软件水印算法,提出一种新的基于PPCT(Planted Plane Cubic Tree)、排序图和中国剩余定理的水印算法DGSW算法。实验仿真表明,使用DGSW水印算法方案的CT软件水印算法在抗攻击能力方面有所提高,同时具有较好的数据嵌入率。
1 动态图软件水印技术
动态软件水印系统评估性能的方式有别于静态软件水印系统。动态水印算法在嵌入水印时要考虑静态数据嵌入率和动态数据嵌入率两种嵌入率。静态数据嵌入率是指在程序中嵌入多少生成水印的额外代码,而动态数据嵌入率是指在程序运行时生成多少额外的数据。此外,动态软件水印算法的隐蔽性分为静态隐蔽性和动态隐蔽性两种。静态隐蔽性是指生成水印的代码的存在是否容易被感知或定位的能力,而如果程序运行时生成的有关水印的数据结构能够与程序原本的数据结构协调一致,那么就说算法是动态隐蔽的。
CT算法需要将水印数字转换成对应的生成图结构的代码,图的结构对水印嵌入率和隐蔽性具有非常重要影响。不同的图编码方案如底数图、排序图等等,单位比特的水印对应的图的大小是不一样的,因此影响了生成水印的代码的体积。而数据嵌入率越低,图对应的水印代码的量越大,水印隐蔽性就越差。所以,文中致力于研究改进CT算法的图编码方案,从而提高算法的数据嵌入率和隐蔽性。
CT动态水印算法的抗干扰能力是一项重要指标,主要取决于算法采用的图编码方式。例如,排序图不能抵抗边翻转攻击,如果攻击者交换其中几条边的顺序,那么图的结构就会完全发生改变,对应的水印数字就不一样了。提出一种新的编码方案DGSW,其抗攻击能力更强,即使图的结构由于攻击被改变,仍然可以发现并纠正错误,从而还原出正确的水印,同时也能够保持较高的数据嵌入率。
2 DGSW算法
2.1 嵌入过程
DGSW使用中国剩余定理,首先构造一个同余方程组把一个水印W分解成一个余数的集合,这些余数代表W的各个片段,只要获得足够多的片段就能恢复出W。算法如下:
(1)选取r个两两互素的数 p1,p2,…,pr,使 W<∏rk=1pk。
(2)把W分解成r(r-1)/2个形如W'≡xkmodpikpjk(0≤xk<pikpjk)的整数。
(3)利用中国剩余定理解出W。
这其中最关键的是,不需要将所有的同余方程都找齐才能够得到最终的水印数字。只要把模数的因子p1、p2、…、pr找全,就能够还原出正确的水印。换句话说,在运气最好的情况下,只需要找到[r/2]个水印片段就能够正确恢复水印。所以在这个例子中,即使这3个片段丢失或者被篡改任意1个,依然有机会计算出正确的水印数字。
通过上述算法获得水印W的各个片段后,需要构造每个水印片段对应的子图并将它们连接。设子图中叶子结点的个数为n,要选取足够大的n使n个结点形成的排序图所表示的数的范围大于子图对应的同余方程的模数,并且叶子结点数为n的PPCT结构所表示的整数范围同样足够大能表示余数。这里采用的选取方法是,根据PPCT结构的特点,计算出最小n,使Calalan(n)>=余数,再计算出最小的n',使n'!>=横数。最后选出max(n',n),作为最终的子图的叶子结点个数,从而构造出对应的图结构。首先构造以下同余方程:
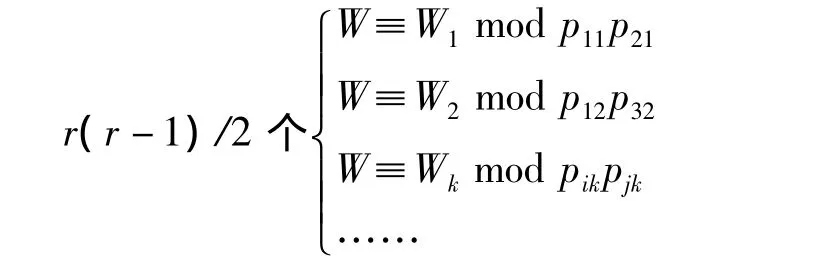
其中0<k≤r(r-1)/2。
利用如下算法可以构造出完整的图结构:
for(each subgraph k)
calculate n1Catalan(n1)≥Wkand n1is minimum
calculate n2PermutaitonGraphLength(n1)≥pikpjkand n2is minimum
n=max(n1,n2)
build PPCT structure according to n and Wk
build Permutaiton Graph
connect each subgraph
下面用一个示例来具体说明嵌入过程。假设要将水印W=25分解成3部分。
(1)首先选取3个两两互质的数,这里选取p1=2、p2=3、p3=5 这3 个数。
(2)接下来把25分解成一个含有3个方程的同余方程组:
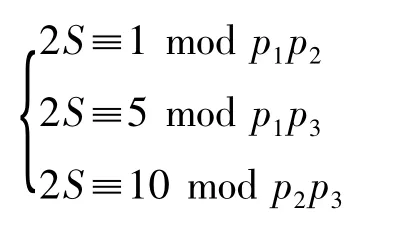
由此计算出1和5、10是水印数字25的3个分解片段。然后根据这3个片段及其对应的模数构造相应的子图,最后连接这3个子图就完成了水印的嵌入过程。同理,在提取水印时,根据图的结构还原同余方程组,再根据中国剩余定理计算出水印。
该同余方程组对应的图结构如下图1所示。
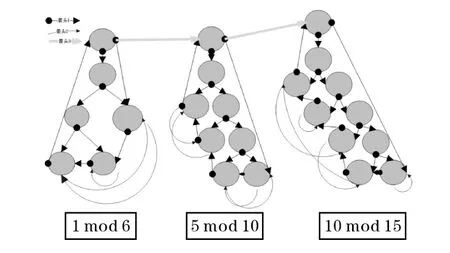
图1 同余方程组结构
余数1对应的PPCT图的叶子结点个数为1,而模数6对应的排序图的结点个数为3,所以选取3作为叶子结点个数构造对应的PPCT结构,再根据排序图编码方案改变叶子结点右指针方向使其表示模数6.依此类推,构造出其他的2个子图。最后把这些子图通过他们的生成结点相连形成一个完整的图结构。
图中箭头都表示图的边,但是作用不同。箭头3用于分割子图,箭头1用于连接子图内PPCT结构的结点。箭头2表示模数。在每个子图内部,各个叶子结点的右指针(箭头2)以排序图的方式编码,用于表示该子图对应的同余方程的模数,而子图的PPCT结构对应这个同余方程的余数。如最左边的子图对应的PPCT结构表示1,而叶子结点形成的排序图表示6。
2.2 提取过程
首先把表示同余方程组的完整图结构分割成若干子图,分析每个子图的PPCT是否完整,然后对每个子图进行解码得到对应的同余方程,进而还原出同余方程组。由于水印可能受到攻击,所以接下来要过滤掉错误的水印片段从而得到正确的同余方程组。办法是首先建立两个图G、H,每一个方程在G、H中都有对应的顶点,并计算出各个子图对应的同余方程,如果两个同余方程不相容(不相容有2种情况,第一种情况指2个方程模数相同但是余数不同,另一种情况是指2个方程的模数中有一个因数相同,但是方程的余数模这个因数得到的余数不同),就在G的对应结点之间建立一条边,如果两个方程相容,就在图H的对应结点之间建立一条边。从图H中找出最大的顶点,因为和这个方程相容的其他同余方程最多,所以这个方程是正确的。接下来将这个顶点对应的方程放到同余方程组U中,并将这个顶点和与它不相容的顶点从H、G中删除,不断重复这个过程直到图G变成一个空图为止。最后应用中国剩余定理就能够计算出同余方程组U表示的水印了。
下面用一个示例具体说明过滤错误片段的过程。已知从各个子图提取出以下同余方程组:
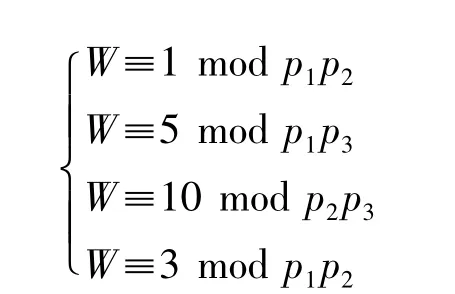
其中 p1=2、p2=3、p3=5。
前3个方程是原来正确的方程,而第4个方程是与原水印不相干的方程。
在图G、H中各构造这4个方程对应的顶点。由于第1个方程与第3个方程不相容,图G中这2组顶点间就有了一条边。只要不断在G中去掉顶点和对应的边,最后就能够去掉第4个方程得到如下同余方程组:
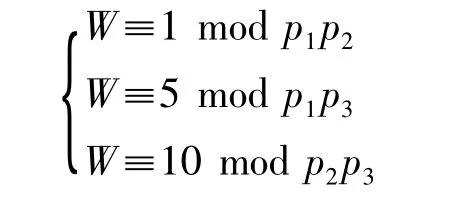
然后拆解同余方程组得到以下方程:
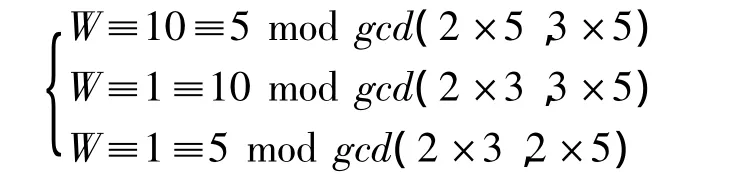
最后利用中国剩余定理解出这个同余方程的解W。
由该方程组可知其中存在很多冗余方程,因此只要把模数的因子p1、p2、…、pr找全,就能够得到还原出正确的水印。在运气最好的情况下,只需要找到[r/2]个水印片段就能够正确恢复水印。所以在这个例子中,即使这3个片段丢失或者被篡改任意一个,依然有能计算出正确的水印数字。
3 仿真测试
3.1 数据嵌入率
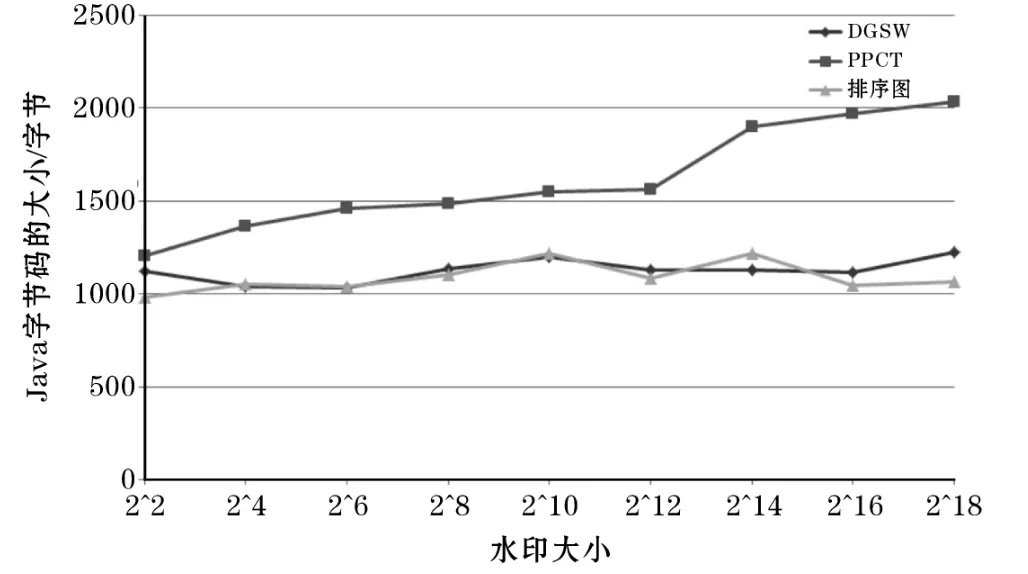
图2 3种编码方案的水印嵌入率
计算DGSW理论上的数据嵌入率不仅比较困难,而且计算结果与实际不太一致,因为CT软件水印算法真正需要的是产生水印图所需代码尽可能地少,而水印图所表示的数尽可能大的一种图,所以通过实验测量单位比特水印对应的图的代码体积是最佳选择。图2显示3种编码方案的水印嵌入率,由图2可知,提出的新编码方案数据嵌入率优于PPCT编码,与排序图相差无几。
3.2 抗干扰能力
3.2.1 抵抗边翻转攻击
该水印算法采用了PPCT结构,因此具有很好抵抗边翻转攻击能力。虽然在新编码方案中叶子结点构成的排序图无法抵御边翻转攻击,排序图所表示的模数会因此改变。根据中国剩余定理,提取水印时只要能够找齐各个模数的因子,就能够正确提取水印,改变少数几个模数的大小并不会影响正确的提取因子。再加上可以在同余方程组中添加冗余方程增强纠错能力,因此,新的编码方案相较于已有的PPCT和排序图的抵抗边翻转攻击的能力都要强。
3.2.2 抵抗结点分裂攻击
结点分裂攻击指把动态分配的内存对象一分为二,变成2个不同的对象,并且让第一个对象指向第二个对象。为了抵抗这种攻击,该编码方案可以转换成一个m次的循环结构,并将所有的边都换成一个m次的链接结构。任何的结点分裂都会融入循环结构或者链接结构当中,提取水印时需要规约这些循环和链接结构,还原出原来的水印图,因此能够自然消除结点分裂带来的影响,如图3所示。
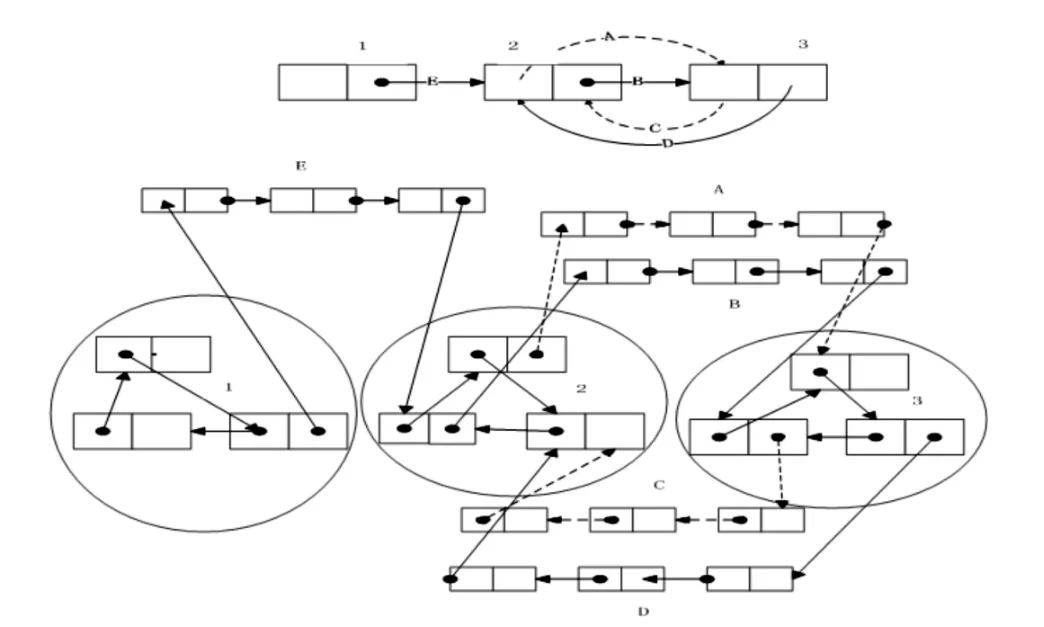
图3 DGSW水印方案抵抗节点分裂攻击
最上面的是一个表示整数3的底数图,在经过循环处理后变成了下面所示的结构。结点1、2、3都变成了3个结点的链接结构,A、B、C 3条边也是如此。即使这样的结构遭受结点分裂攻击,在最后还原水印图时攻击产生的影响都能够被消除。
3.3 隐蔽性
由于对具有海量且复杂链接的数据结构的程序进行别名分析是非常困难的,所以CT算法具有很好的动态隐蔽性。然而CT算法本身并不能保证水印的静态隐蔽性,所以必须使用代码混淆等保护技术使得程序源代码可分析性降低。因此需要通过实验判断现有的代码混淆技术是否会对CT算法的水印的提取产生影响。
以下测试的是本编码方案抵抗代码混淆处理的能力。其中“+”表示能够抵御混淆处理,水印能够正常提取,”-“表示不能抵御混淆处理。修改比例指程序中混淆的方法数占总方法数的比例。

表1 代码混淆技术对水印提取的影响
由表1可知,除了Split Classes这个混淆算法之外,其余的混淆算法对水印的提取没有任何影响。
4 结束语
在CT算法的现有编码方案基础上,综合中国剩余定理和现有编码方案的一些优点提出DGSW编码方案。实验结果表明这套编码方案具备抗攻击能力强,纠错能力好,数据嵌入率较高的优势。
[1] Davidson R I,Myhrvold N.Method and system for generating and auditing a signature for a computer program:US,US5559884 A[P].1994.
[2] Hattanda K.The evaluation of Davidson's digital signature scheme[J].Ieice Transactions on Fundamentals of Electronics Communications&Computer,2004,87(87-A):224-225.
[3] Myles G,Collberg C,Heidepriem Z,et al.The evaluation of two software watermarking algorithms.[J].Software Practice & Experience,2005,35(10):923-938.
[4] Myles G,Collberg C,Heidepriem Z,et al.The evaluation of two software watermarking algorithms[J].Software Practice & Experience,2005,35(10):923-938.
[5] Moskowitz,Scott A,Cooperman Marc.Method for stega-cipher protection of computer code[M].U-nited States Patent 5745569,1996.
[6] Collberg C,Thomborson C.Software watermarking:Models and dynamic embeddings[C].In:Principles of Programming Languages 1999,POPL 1999.
[7] Collberg C S,Thomborson C,Townsend G M.Dynamic graph-based software fingerprinting[J].Acm Transactions on Programming Languages&Systems,2007,29(6):695-706.
[8] Palsberg J,Krishnaswamy S,Kwon M,et al.Experience with software watermarking[C].Proceedings of Acsac Annual Computer Security Applications Conference,IEEE Computer Society,2000:308.
[9] Nagra J,Thomborson C.Threading Software Watermarks[J].Lecture Notes in Computer Science,2004:208-233.
[10] Collberg C S,Thomborson C.Watermarking,Tamper-Proofing,and Obfuscation-Tools for Software Protection[J].Software Engineering IEEE Transactions on,2002,28(8):735-746.
[11] Christian Collberg,Jasvir Nagra.软件加密与解密[M].北京:人民邮电出版社,2012:432-443.
