一种考虑非视距传播的UWB定位算法

苏应敢，张林山，姚建，王彦

(1.云南电网有限责任公司西双版纳供电局，云南 景洪 666100；2.云南电网有限责任公司电力科学研究院，昆明 650217)

一种考虑非视距传播的UWB定位算法

苏应敢1，张林山2，姚建1，王彦2

(1.云南电网有限责任公司西双版纳供电局，云南 景洪 666100；2.云南电网有限责任公司电力科学研究院，昆明 650217)

提出了一种考虑非视距 (NLOS)传播的基于TOA的UWB定位算法。其主要思想为采用一个新的变量替换定位估计中的两次项，把非线性估计转化为两次最大似然估计，并通过引入松弛变量和采用搜索的方法，消除NLOS传播对定位算法精度的影响。此算法结构简单，计算量不大，在工程应用中容易实现，最重要的是该算法的计算结果和原有的算法比较具有更高的精度。

NLOS；UWB；定位算法；最大似然估计；TOA

0 前言

当前所应用的UWB传感器网络定位系统中，测电磁波到达时差值 (TDOA)和测电磁波到达时间值 (TOA)相对易于得到，基于TDOA和TOA的定位方法具有较好的定位性能，故对UWB传感器网络定位系统的定位多是集中在这两种基于测距的定位技术上，但是，在很多的实际应用中，由于测量数据会受到非视距传播 (NLOS)的影响，从而导致定位方程的求解往往会产生很大的误差，甚至得不到定位目标的坐标值，定位系统的性能将会受到很大挑战[1]。

处理非视距 (NLOS)传播影响信号测量的准确性的问题，TOA方法能更好地降低NLOS所造成的误差的影响。目前，经典的TOA定位方法有文献 [2]的LLOP(Linear Line of Position)方法，它将3个圆相交转化为2条相交线相交，通过多次测量求解，得到多个测量交点，并求出它们的质心以确定目标的位置，此方法至少需要三个基站。另外，文献 [3]提出的 RSA(Range Scaling Algorithm)方法，它利用尺度因子表示与真实距离的接近程度，虽然定位精度有很大改善，但仍不能满足要求。文献 [4]提出了一种精度较高的两步最大似然 (ML)TDOA估计方法，但它是在非视距 (NLOS)传播干扰影响较严重时不是很有效。目前，在多径传播环境中，一般将所能分离出来的多径支路中最早到达接收机的支路的传输时延作为信号的TOA。由于上述的一系列算法都没有考虑NLOS传播干扰对定位的影响，在NLOS干扰严重时，这些算法均会失效。因此，本文提出了一种考虑NLOS传播的UWB定位算法。

1 不考虑NLOS的UWB定位算法

如图1所示，在三维空间中分布着M个锚点，从目标节点 (x，y，z)发射的信号到达第i个锚点的TOA为Ti，在多径环境下，Ti为信号最早到达锚点的支路的传输延时，它可以通过采用扩展Kalman滤波器[5]或其它方法估计得到，因此，在视距传播时有：

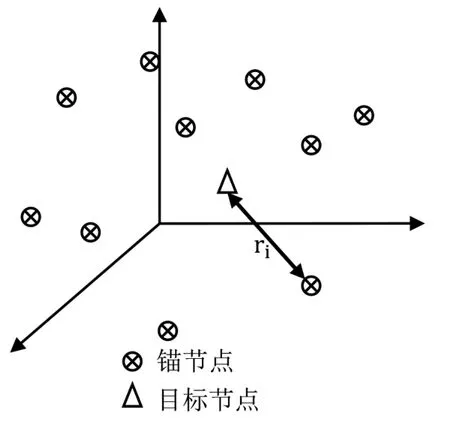
图1 三维空间定位

上面式 (2)中，为电磁波的传播速度。令R

在式 (3)中，令Za=[x，y，z]T，则误差矢量为：

其中：

如果将真实值表示为：r01，r02，…，r0M测量值表示为：r1，r2，…，rM，则ri=r0i+cΔTi，误差矢量表示为：

用最大似然法对式 (4)进行估计可得：

在式 (7)中，Q为估计噪声的协方差矩阵，B在估计时为未知数，可先用测量值r1，r2，…，rM代替r01，r02，…，r0M估计出一个初始坐标值，然后用此初始解算出对应的BB，再将由式 (7)求出Ø代入式 (6)求出更精确的解。如上进行迭代，知道得到与实际值足够逼近的估计值。

对应Za的协方差矩阵为：

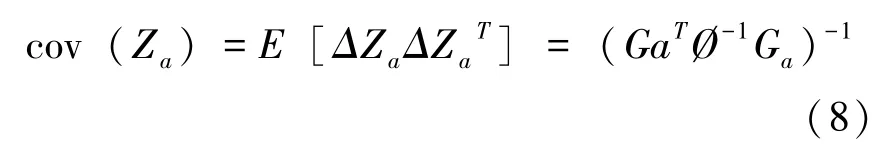
上面的情况是在假设x，y，z，R无关的情况下求解的，但是在实际应用中它们之间是有一定关系的，下面我们将结合这种关系进行更好的估计。假设x，y，z，R的估计误差分别为e1，e2，e3，e4，则有：

将 (10)式代入 (9)式，可得：

式 (11)是e1，e2，e3在非常小的情况下获得的，此时φ′的协方差矩阵为：

其中：B′=diag{x0，y0，z0，0.5}，B′元素可用Za中元素x，y，z的近似值得到，类似地，zp的最大似然估计为：

2 考虑NLOS影响的TOA算法

在实际应用中，如在变电站安全区域三维定位系统中，由于变电站内电器设备密集区内障碍物较多，从目标节点到锚点发出的信号，往往不能直接到达，而是要通过反射或穿透，其测试路径距离必然比直射路径长，如仍用上述方法计算，所引起的误差可能会超出接收的范围，此时必须考虑NLOS传播对定位精度的影响。当存在NLOS传播时，上面式 (3)变为：

在式 (14)加入松弛变量，可变为等式：

显然，在式 (15)组成的方程组中有M+4个未知数，因此，这是个不定方程组。若任采用前面所使用的最大似然估计法进行求解，必然会使得系数矩阵奇异。在此我们只考虑将其中的个松弛变量作为未知量，将剩下的4个松弛变量作为已知，于是有：

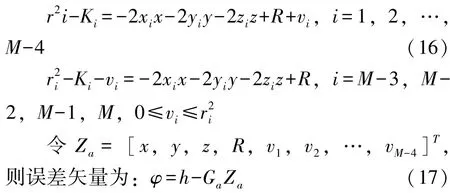
其中：

用最大似然法对式 (17)估计得：

Q为估计噪声的协方差矩阵，在实际应用中，可将不考虑NLOS干扰的TOA算法估计出的一组值作为式 (19)中的初值，然后运用重复迭代法获得更高精度的值。显然，由上面所计算Za的是一个关于vM-3，vM-2，vM-1的函数，Za可分解为：

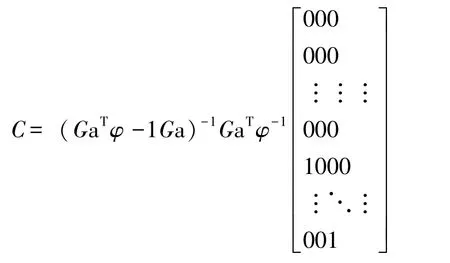
由于 v1，v2，…，vM-4都可以表示为关于vM-3，vM-2，vM-1，vM的函数，所以方程组 (15)中的限制条件0≤vi≤r2i可转化为：

其中：C′=C(5：M，1：3)，Z′ac=Zac (5：M，1：3)

大部分情况下，式 (21)所定义的解空间范围比较大，从而导致解空间中一些解与目标节点的真实值相差很大，因此我们需要在此解空间中找到最大程度的与目标位置接近的解。假设上面不考虑NLOS传播时计算出的目标节点为 (x′，y′，z′)，则此问题可转化为一求最优解的问题：

min{(x-x′}2+(y-y′)2+(z-z′)2}，式( 2 1 )为限定条件，其中：

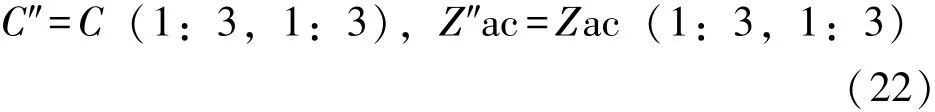
对式 (22)的最优化问题求解，然后将其解代入式 (20)求出Za及其协方差矩阵cov (Za) =E[ΔZaΔZaT] =(GaTφ-1Ga)-1(23)

同样，x，y，z，R在实际应用中它们之间是有一定关系的，下面我们将结合这种关系进行估计。假设x，y，z，R的估计误差分别为e1，e2，e3，e4，则有Za(1)=x0+e1，Za(2)=y0+e2，Za(3)=z0+e3，Z(4)=R0+e4(24)

设矢量误差φ′=h′-Ga′Zp (25)

将式 (24)代入式 (25)，可得

上式在e1，e2，e3非常小时成立，则此时φ′的协方差矩阵为：

其中：B′=diag{x0，y0，z0，0.5}，P=cov (Za)(1：4，1：4)

则类似地，Zp的最大似然估计为：

3 结束语

本文在原有的最大似然估计目标节点位置的基础长，引入了松弛变量，采用迭代计算的方式进行计算，消除了NLOS传播对定位算法精度的影响，此中算法结构简单，计算量不大，易于实现，对于类似于变电站电器设备密集区一样复杂的环境，可以实现更精确的定位，具有很强的理论和实践意义。

[1] 陈健，卓永宁.一种基于TOA的定位优化算法 [J].无线电通信技术，2010，36(4)：52-54

[2] CAFFERY J.A new approach to the geometry of TOA location [C].IEEE VTC2000 Fall September 24-28，Boston，USA，2000：1943-1949.

[3] HUANG Y T.An Efficient Linear-correction Lesat-squares Approach to Source Localization[C].IEEE Workshop on the Applications of Sjgllal Processing to Audio and Acoustics，2001：67-70.

[4] SMITH J O，ABEL J S.Closed-form least-squares source location estimation from range difference measurement[J].IEEE Trans AcoustSApeech，Signal Processing，1987，ASSP-35 (12)：1661-1669

[5] 王昕，王宗欣.用扩展Kalman滤波器计算多径下两路间时延 [J].复旦学报 (自然科学版)，2000，39(2)：193 -200

Research on a UWB-based Location Algorithm Considering NLOS Propagation

SU Yinggan1，ZHANG Linshan2，YAO Jian1，WANG Yan1
(1.Xishuangbanna Power Supply Bureau，Yunnan Power Grid Co.，Ltd.，Jinghong，Yunnan 666100，China；2.Yunnan Electric Power Research Institute，Yunnan Power Grid Co.，Ltd.，Kunming 650217，China)

This paper put forward one UWB location arithmetic based on TOA，which including the influence of non-line-sight (NLOS)propagation.The main idea of this paper is to use a new variable to replace the square variable，translate nonlinear estimation into twice maximum likelihood estimation，introduce relaxation variables and use search method to eliminate the influence of NLOS to location accuracy.This arithmetic has simple structure，small computation，and achieves easily，and especially it has better accuracy comparing old arithmetic.

NLOS；UWB；location arithmetic；maximum likelihood estimation；TOA

TM74

B

1006-7345(2015)06-0095-04