船舶复杂混合动力推进轴系振动研究

杨 震，肖 能齐，周瑞平，林 晞 晨

（武汉理工大学能源与动力工程学院，武汉430063）

0 引言

船舶混合动力推进系统主要是由机械推进系统部分和电力推进系统组成[1-3]。混合动力推进系统与传统的推进系统相比较，结构、功能更加复杂，使得复杂混合动力推进轴系的振动研究存在大量未解决或值得考虑的问题。本文以某船舶混合动力推进轴系为研究对象，分析其运行工况及振动机理，建立混合动力推进系统振动数学模型并进行振动计算，对混合动力推进系统的低噪声设计理论研究及工程设计具有一定的指导意义。

1 复杂混合动力推进系统

该推进系统为四机双桨混合动力推进系统，其由2台9L48/60B柴油机I（功率为10350 kW,转速为514 r/min）、2台6L48/60B柴油机II（功率为6900 kW,转速为514 r/min）、2台GWVH减速齿轮箱、1台轴带发电机(PTO)、1台电动机（PTI）、传动轴系、2个螺旋桨、变频器和配电板等组成。如图1所示的某船舶四机双桨+PTO/PTI复杂混合动力推进轴系示意图。

该推进系统具有多种运行工况，根据其营运工作模型可以划分为单机模式、双主机并车模式和PTI模式三类，如表1所示。该系统在PTI模式下带有轴带发电机推进系统的柴油机I或者柴油机II运行，通过传动轴系驱动螺旋桨工作；同时轴带发电机发电机发电经配电板驱动电动机（PTI）运动，通过传动轴系驱动螺旋桨工作。该PTI模式中驱动电动机的电力来源于推进柴油机，而非柴油发电机。

图1 某船舶四机双桨+PTO/PTI复杂混合动力推进系统示意图

2 数学模型的建立与振动机理研究

2.1 扭转振动机理研究与模型的建立

图2 柴 油机 I-齿 轮箱-螺 旋桨+轴 带发电机(P TO)+电 动机(P TI)当量系统图

复杂混合动力推进轴系扭转振动与传统的推进轴系扭转振动相比，前者在计算过程中涉及的因素更多，振动机理更加复杂，因此对其进行更加精确的计算显得更加重要。复杂混合动力推进轴系扭转振动激励源包括考柴油机气体压力和惯性力作用产生的激励力矩、螺旋桨不均匀伴流场产生的激励力矩以及电机运行过程中所产生的电磁激励力矩对轴系扭转振动的影响[4-6]。

根据表1所示的推进系统工作模式及轴系扭振激励源的分类，主要研究PTI模式Mod7、单机模式Mod3和双机双桨模式Mod6三种运营模式。根据轴系扭振当量系统集总参数模型的简化原则，可以得到上述三种工作模式下的复杂混合动力推进系统的扭转振动当量系统模型，如图2-4所示。特别强调对于第三种工作模式柴油机仅为电动机运行提供电力来源。

2.2 回旋振动及校中机理研究与模型的建立

船舶推进轴系回旋振动的激励力主要包括旋转螺旋桨的不平衡离心力、螺旋桨上流体激振力以及螺旋桨偏心质量产生的激振力[7-8]。对于带齿轮箱传动轴系，按照回旋振动计算模型简化原则从轴系螺旋桨至传动齿轮箱大齿轮而组成的含有若干集中参数的链状分布系统。

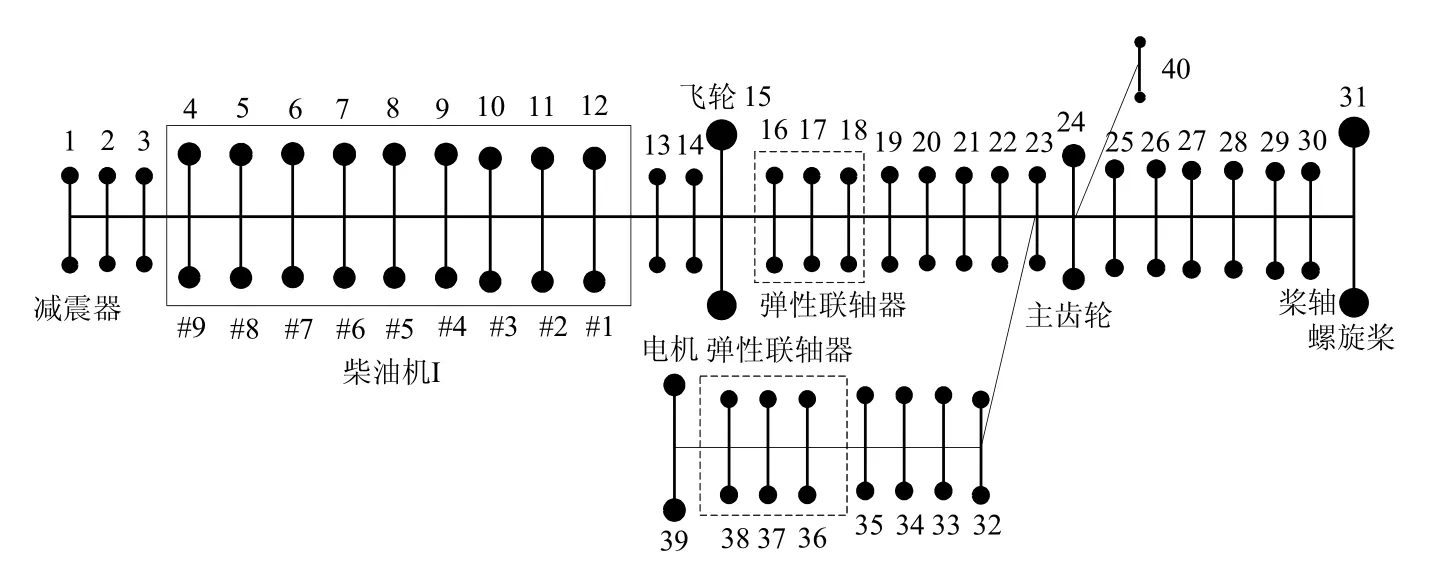
图3 柴油机 I-齿 轮箱-螺 旋桨+轴 带发电机(P TO)当量系统图

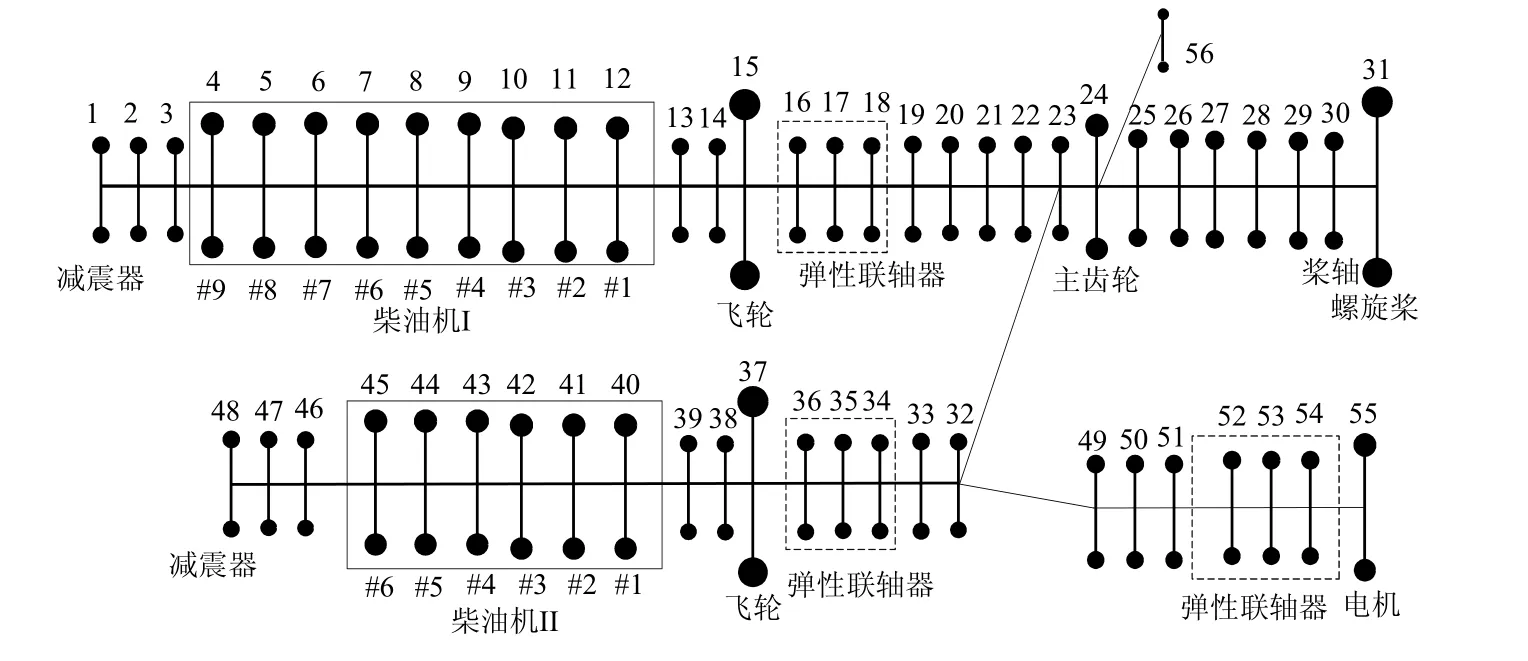
图4 柴 油机I和 II-齿 轮箱-螺 旋桨+轴 带发电机(P TO)当量系统图

表1 四机双桨+PTO/PTI复杂混合动力推进系统工作模式

表2 柴油机I-齿轮箱-螺旋桨+轴带发电机(PTO)+电动机(PTI）自由振动计算结果

表2 柴油机I-齿轮箱-螺旋桨+轴带发电机(PTO)+电动机(PTI）自由振动计算结果

在轴系校中过程中，不合理的轴系校中将会使轴系各支撑轴承的负荷受力不均，将会引起机体振动和轴承异常磨损，更严重将会导致轴折断等事故。对于带齿轮箱传动轴系，轴系校中一般将轴系简化为多个弹性或者刚性支撑的连续梁[9]，从螺旋桨端简化之传动齿轮箱轴。

通过上述分析分析，可以得到用于回旋振动和轴系校中推进系统数学模型，如图5所示的某船舶四机双桨+PTO/PTI复杂混合动力推进系统模型。

图5 某船舶四机双桨+PTO/PTI复杂混合动力推进系统模型

3 复杂混合动力推进轴系振动计算与分析

3.1 扭转振动计算与分析

根据扭转振动基本理论，采用系统矩阵法建立轴系扭转振动一般方程：

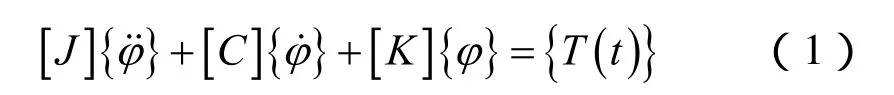
式中：［J］为转动惯量矩阵；［C］为阻尼矩阵；［K］为刚度矩阵；和｛φ｝分别为扭转角加速度、角速度和角位移； ｛T（t）｝ 为激励力矩。

PTI模式Mod7柴油机I-齿轮箱-螺旋桨+轴带发电机(PTO)+电动机（PTI）运营模式下，自由振动计算结果如表2所示而强迫振动计算结果如图6和图7所示。

图6 第 13号 质量点(弹 性联轴器)功率损失曲线

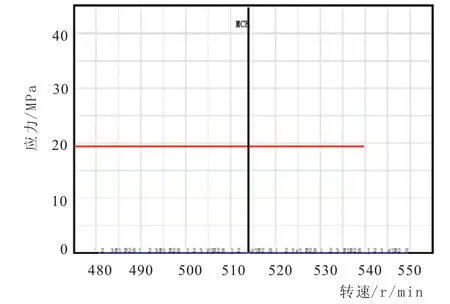
图7 第 2号 质量点(螺 旋桨轴)应力曲线

图9 单 机模式 M od3工况的自由振动值

单机模式 Mod3柴油机 I-齿轮箱-螺旋桨+轴带发电机（PTO）运营模式和双机双桨模式Mod6柴油机 I/II-齿轮箱-螺旋桨+轴带发电机（PTO）运营模式下，其自由振动计算结果如图9所示的双机双桨模式Mod6工况的自由振动计算值；而单机模式Mod3工况强迫振动计算结果如图11和图13所示，双机双桨模式Mod6工况强迫振动计算结果如图11-图16所示。

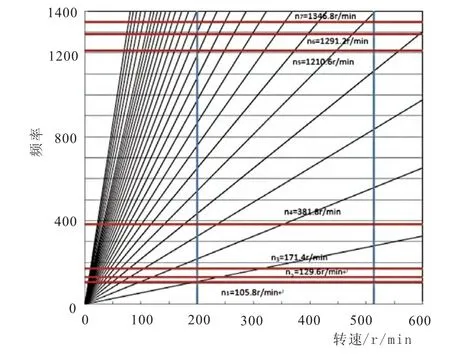
图10 双机双桨模式 M od6工况的自由振动值

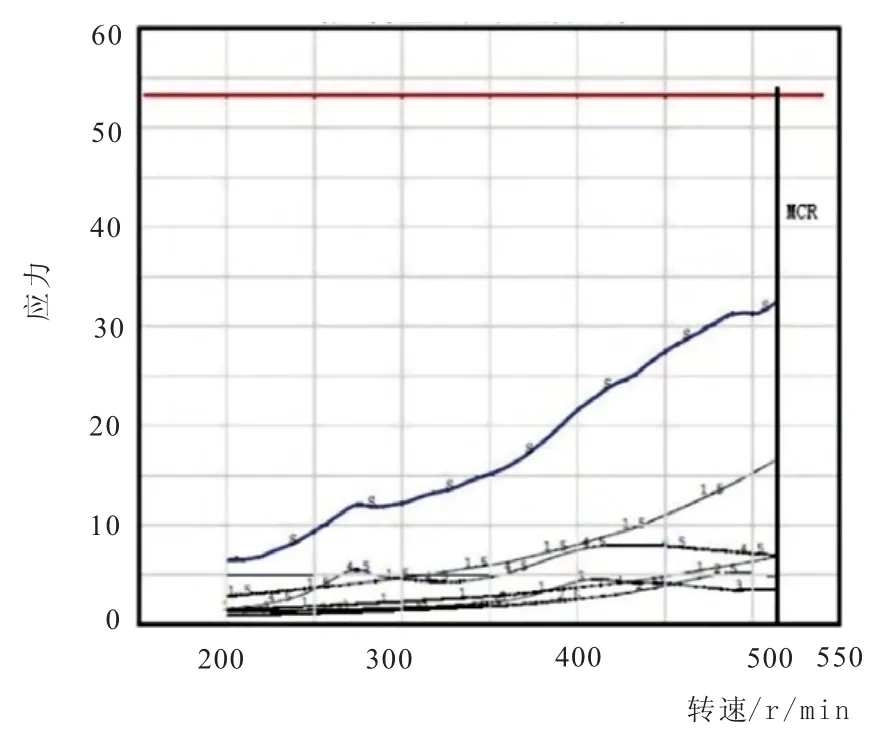
图11 第 8号 质量点(曲 轴)应力曲线

通过采用系统矩阵法对复杂轴系混合动力推进系统扭转振动进行计算可知：PTI模式Mod7电力推进轴系在工作转速范围内，系统振动振幅远小于许用值；单机模式Mod3和双机双桨模式Mod6在工作转速范围内，存在明显的共振点，但是未超过许用值，满足规范要求。

3.2 回旋振动及校中计算与分析

在轴系校中计算过程中，目前传统校中计算方法主要有有限元法、传递矩阵法和三弯矩方程法，其理论基础均是经典力学方法。复杂混合动力推进系统比传统轴系更为复杂，在轴系校中计算更加完善且更加符合实际工程，提出采用改进三弯矩法进行复杂混合动力推进系统轴系校中[9]，其轴系校中结果如图1所示。

图12 第 1 6号 质量点(弹 性联轴器)功率损失曲线

图13 直 线状态下轴承各负荷值(单 位kN)

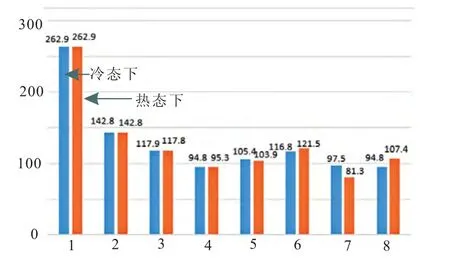
图14 冷态状态和热态下轴承各负荷值(单 位kN)

根据图17直线状态下轴承各负荷值齿轮箱后艉轴承8和前艉轴承7的负荷之差110.7kN，很显然不满足规范要求。调整齿轮箱后艉轴承和前艉轴承变位为2.0 mm和2.71 mm，可以得到冷态各轴承负荷如图18所示，各轴承负荷均满足规范要求，齿轮箱后艉轴承和前艉轴承负荷只差仅2.7 kN；在热态下考虑齿轮箱热膨胀0.25 mm后，各轴承负荷均也满足规范要求，如图18所示。

在轴系回旋振动计算过程中，传统Myklestal-Prohl传递矩阵法具有表达式简单、易于编程求解等，适用于解决简单的传统推进轴系。由于复杂混合动力推进系统具有轴系较长、支撑轴承较多等特点，若采用Myklestal-Prohl传递矩阵法可能产生数值不稳定现象，因此为提高复杂轴系回旋振动计算精度，本文采用Riccati传递矩阵法进行求解。该复杂船舶混合动力推进轴系回旋振动计算结果如表3所示。

由于混合动力推进轴系工况较多，频率范围较宽；在进行回旋振动计算过程中，在PTI模式Mod7工况下轴系产生共振点。共振点的产生除轴系工况较多外，由于混合动力推进轴系系统往往被用于一些大型化船舶中出现，船体尾部的刚度将有所降低，轴系有产生共振的可能性。为了提高船舶的推进效率，混合动力推进轴系往往采用多桨推进轴系；则轴系必然有一部分将远离船体伸入水中采用舷外托架支撑，其刚度一般要比船体内的支撑刚度低，轴系有产生共振的可能性。

4 结论

1）船舶复杂混合动力推进轴系在进行扭转振动过程中，其计算工况较多且扭振数学模型较复杂；同时扭振激励复杂需综合考虑才能使扭转振动计算更为精确。2）在复杂混合动力推进轴系设计阶段，轴承布置不仅需要满足轴系合理校中；同时由于混合动力推进轴系工况较多，频率范围较宽，可能很难避免回旋振动共振点的产生，因此设计阶段需尽可能使回旋振动共振点较少且落在不常运行的工况。

[1]周瑞平,肖能齐,赵同宾,林晞晨.混合动力推进系统低噪声轴系设计研究进展[J].武汉理工大学学报(交通科学与工程版),2014,38(3):488-491.

[2]Völker T.Hybrid propulsion concepts on ships[J].Zeszyty Naukowe Akademii Morskiej w Gdyni,2013.

[3]Simon Sortland.Hybrid propulsion system for anchor handling tug supply vessels[J].WÄRTSILÄ TECHNICAL JOURNAL，2008，(01):45-48.

[4]王磊.船舶复杂推进轴系扭振机理及计算软件研究[D].武汉理工大学,2011.

[5]W.J.HSUEH.On the vibration analysis of multi-branch torsional system[J].Journal of Sound and Vibration,2007,232(2):209-220.

[6]肖能齐,周瑞平,林晞晨.冰区航行船舶电力推进轴系机电耦合的扭振分析[J].船舶工程,2015,37(4).