一种适用于虚拟惯量优化控制研究的风电场等值建模方法

陈宇航，袁 阳，邢鹏翔

(1.海军驻葫芦岛四三一厂军事代表室，辽宁葫芦岛 125004； 2.武汉大学电气工程学院，武汉 430072)

0 引言

随着风力发电技术的日趋成熟，电力系统中风电所占比例不断提高。

本文简要分析了直驱式风电机组运行特性和虚拟惯量控制原理，基于直驱式风电单机并网详细模型，利用Matlab/Simulink软件建立便于进行多机聚合的简化模型，将风电场中的机组按风速分群，不同风速区群内机组各自聚合为等值机组，各等值机组并联即得到多机等值风电场模型。通过与详细仿真模型对比，验证了等值模型的有效性。

1 直驱式风电并网系统结构和运行特性

1.1 直驱式风电机组详细模型

直驱永磁风力发电并网系统主要包括风力发电机、全功率变流器、并网变压器、电网、负荷及其控制系统。风力机和永磁同步发电机（PMSG）通过轴系直接耦合，再经全功率变流器与电网相连，如图1所示。

图1 直驱式风电并网系统结构

风力机通过风轮捕获风能驱动PMSG发电，风力机捕获的机械功率Pwind的表达式为

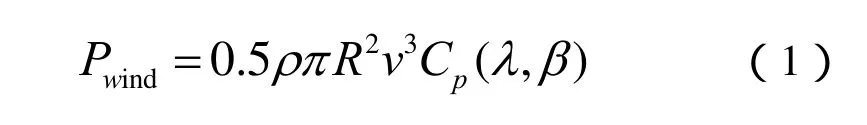
式中ρ为空气密度，R为风轮的半径，v为向上自由风速，Cp为风力机的功率系数，它是桨距角β和为叶尖速比γ的函数，λ=ωwR/v，ωw为风力机风轮的转速。通常，当机组出力小于限定功率时，桨距角β将控制为0。此时Cp仅为λ的函数，在一定风速下通过调整发电机的转速ωw可令Cp达到最优值Cpmax，即实现最大功率跟踪（MPPT）控制[9]。这时所对应的叶尖速度比γ为γop，风力机析取风能为

其中kmax为风力机析取最大风能时对应的系数，其数值为 0.5ρπR5Cpmax/λopt3。

当风速较大使得风机转速超过额定值时，桨距角控制系统将开始动作，机组通过增大桨距角，减小风力机捕获的机械功率，从而降低机组转速[10]。桨距角控制系统如图2所示。

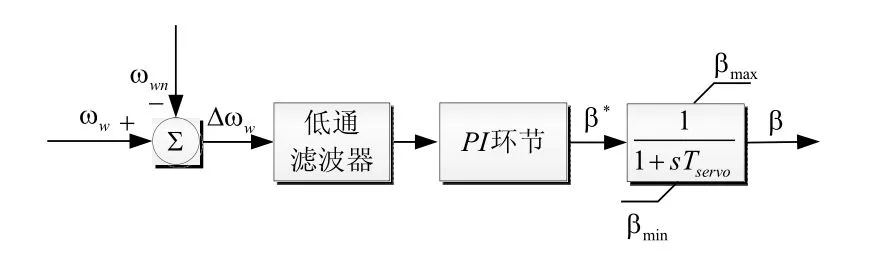
图2 桨距角控制系统

直驱式风力发电机组传动系统用单质块模型等效表示，这里认为传动轴为刚性、忽略轴系暂态行为，有

式中，Jw为 D-PMSG的转动惯量，ωw为风力机的机械角速度，D为机组的机械阻尼系数，PR为机侧变流器的输入功率，其参考值为Pwref。

dq轴下的永磁同步发电机数学模型如下[11]（参数含义见附录）：

全功率变流器包括机侧整流器和网侧逆变器两部分。机侧变流器实现MPPT控制、虚拟惯量控制及PMSG机端电压控制，网侧变流器实现对直流母线电压及无功出力的控制。

电网部分由一台等值同步发电机和等值负载组成，仿真模型中该发电机采用详细模型。

1.2 比例-微分（PD）虚拟惯量控制原理

虚拟惯量控制是转子动能控制法的一种，利用全功率变流器有功功率快速调节的特性，在MPPT控制基础上附加调频辅助功率，可使风电机组响应系统频率变化，将部分转子动能转化为电磁功率注入电网，从而参与调频。当调频辅助功率与系统频率偏差的比例和微分量相关时称为PD虚拟惯量控制，其控制原理结构图如图3所示。

上图中，直驱式风电机组并入由传统同步发电机组和负荷组成的等值电网中，风电机组通过虚线框内的 PD虚拟惯量控制环节参与频率响应，虚拟惯量控制的调频辅助功率为Ps

图3 D-PMSG 虚拟惯量控制原理结构图

kp和kd分别为系统角频率偏差值的比例和微分系数，p为微分算子[12]。kp>0，kd<0。在虚拟惯量控制方式下，全功率变流器有功功率外环控制的参考值Pwref由MPPT控制功率附加调频辅助功率得到

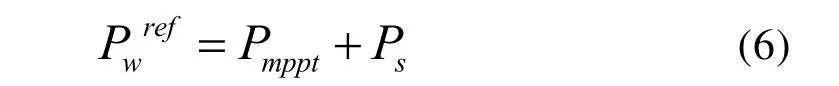
当电力系统正常运行时，调频辅助功率值为0。当系统因电源或负荷的突增或突减而导致频率变化时，直驱式风电机组可通过 PD虚拟惯量控制响应该变化，得到相应的调频辅助功率值。辅助功率的大小与系统频率变化量和变化速度有关。

2 直驱式风电单机并网模型的简化

利用上节详细仿真模型进行风电场虚拟惯量优化控制研究时，存在仿真耗时长、频率动态响应受系统规模限制、等值后全功率变流器容量过大等问题，因此在保留虚拟惯量控制过程中风电机组典型变量响应过程的前提下，有必要对详细仿真模型进行适当简化。

2.1 简化思路

直驱式风电机组输出的电磁功率由变流器控制决定，由于风电并网系统频率稳定性研究主要针对机电暂态过程，而电磁暂态过程远快于机电暂态过程，因此可忽略PMSG和变流器的电磁调节过程，将其等效为一个惯性环节[12,13]：

Ts为发电机组和变流器的等效惯性时间常数，约为 0.2 s。

在直驱式风电单机并网简化仿真模型中，PMSG和机网侧变流器用惯性环节代替，忽略PMSG和变流器损耗，机侧变流器有功功率外环参考值经惯性环节后即得到并网电磁功率，其取值与永磁同步发电机组输出电磁功率PR相等。简化后的风电机组模型通过惯性环节仅向电网输送有功功率，直驱式机组和电网通过受控电流源进行接口，最终得到直驱式风电单机并网简化模型。电流源输出的三相交流电流Iabc的相位由 PCC点电压锁相得到，其幅值由PR及电网母线电压幅值决定，具体计算为：

其中VSG为并网母线电压有效值标幺值，VB为基准电压，VB=400 V。模型具体见图4：直驱式风电单机并网简化模型实现了单位功率因数注入，在保证有功功率平衡的前提下有效地对复杂的永磁同步发电机和全功率并网变流器进行了简化，适用于风电并网频率稳定性研究。

2.2 风电机组简化仿真模型的校验

实际风电场参与系统频率调整时会遇到风速扰动和负荷扰动两类常见扰动。

1）负荷扰动情况

仿真条件：考虑风力机的虚拟惯量控制，风速恒定10 m/s，在40 s时系统负载由3.65 MW增加至4 MW。直驱式风电机组详细和简化仿真模型典型系统变量的动态响应对比情况如图5示。

2）风速扰动情况

仿真条件：不考虑风力机的虚拟惯量控制（风电机组不参与系统频率调整），初始风速 11.36 m/s，系统负载恒定3.65 MW，在40 s时风速由11.36 m/s降为10.65 m/s。

3 风电场内机组的分群和聚合

风电场出力特性与单台风电机组出力特性有很大不同，因此在进行风电场等值建模时，既要考虑风电机组动态特性，又要考虑机组分布特性和机组间耦合特性[14-16]。风电场中各机组运行状态各异，采用多机等值方法可以更好地反映实际风电场的状态，且具有更高的精度。

3.1 分群和聚合思路

在对风电场进行多机等值前需确定分群指标，以体现风电机组的分布特性。由于各个机组所接受的输入风速不同，可选取最能体现直驱式风电机组特性的代表风速，然后按代表风速进行风电场分群。某直驱风电机组风速-功率特性曲线如图7所示[7]。

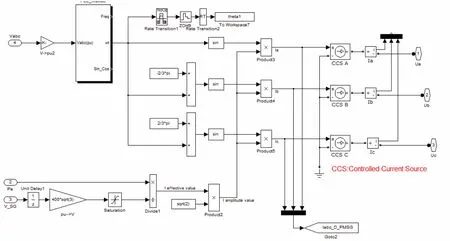
图4 直驱式风电单机简化模型与电网接口

由图5可知，D-PMSG的运行区间可以分为低风速、中风速和高风速三个区间，在每个区间内，D-PMSG风速-功率特性呈近似的线性特性。为使多机等值风电场模型涵盖上图示的三个区域，这里选取的分群代表风速为：风电场参与调频的最大风速，风电场参与调频的最小风速，风电场平均风速。最大风速和最小风速由实测得到，平均风速由以下方法求得：通过风速-功率曲线，求得风电场最大风速下的输出功率Pmax，以及最小风速下的输出功率Pmin，则求得其平均功率Pavg=(Pmax+Pmin)/2，再通过风速-功率曲线求取在Pavg处对应的风速，作为平均风速。

分群代表风速选取完后，对风电场内的机组按代表风速进行分群：风速小于最小风速测量值的归为低风速群，风速大于最大风速测量值的归为高风速群，风速在最大测量值和最小测量值之间的归为中风速群，从而得到三群风电机组，各群风速值取相应的代表风速，同群机组聚合为等值机组。等值过程以等值机的风力机与单台风电机组风力机的功率转换特性不变为原则，等值风力机机械功率为同群风力机机械功率之和，等值机组轴系相关参数由同群机组相加得到，由于永磁同步发电机和变流柜已等效为一阶惯性环节，等值机组输出电磁功率参考值为同群各机组电磁功率参考值之和。当同群机组均为同一型号时，具体方法是：

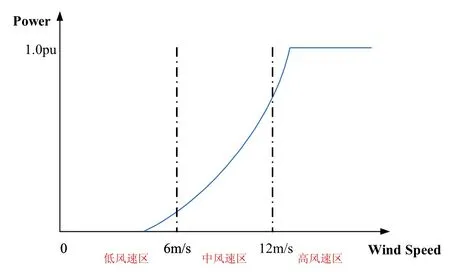
图5 直驱风电机组功率-风速特性曲线

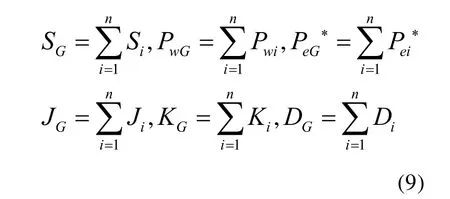
式中：S、Pw、eP*为风机的容量、机械功率、电磁功率参考值；J、K、D为轴系转动惯量、刚度系数、阻尼系数[19]，下标G代表等值参数。

将高、中、低三风速下的等值机组并至电网即可得到直驱式风电场三机等值模型。

3.2 同风速群机组聚合等值模型校验

1）负荷扰动情况

仿真条件：考虑风力机的虚拟惯量控制，风速恒定10 m/s，相同风速下的机组3台，在40 s时系统负载由7 MW增加至8 MW。

三台直驱式风电机组聚合等值前后型系统变量的动态响应对比情况如图6所示。

2）风速扰动情况

仿真条件：不考虑风力机的虚拟惯量控制，初始风速11.36 m/s，系统负载恒定7 MW，相同风速下的机组3台，在40 s时风速由11.36 m/s降为10.65 m/s。

3台直驱式风电机组聚合等值前后型系统变量的动态响应对比情况如图7所示。

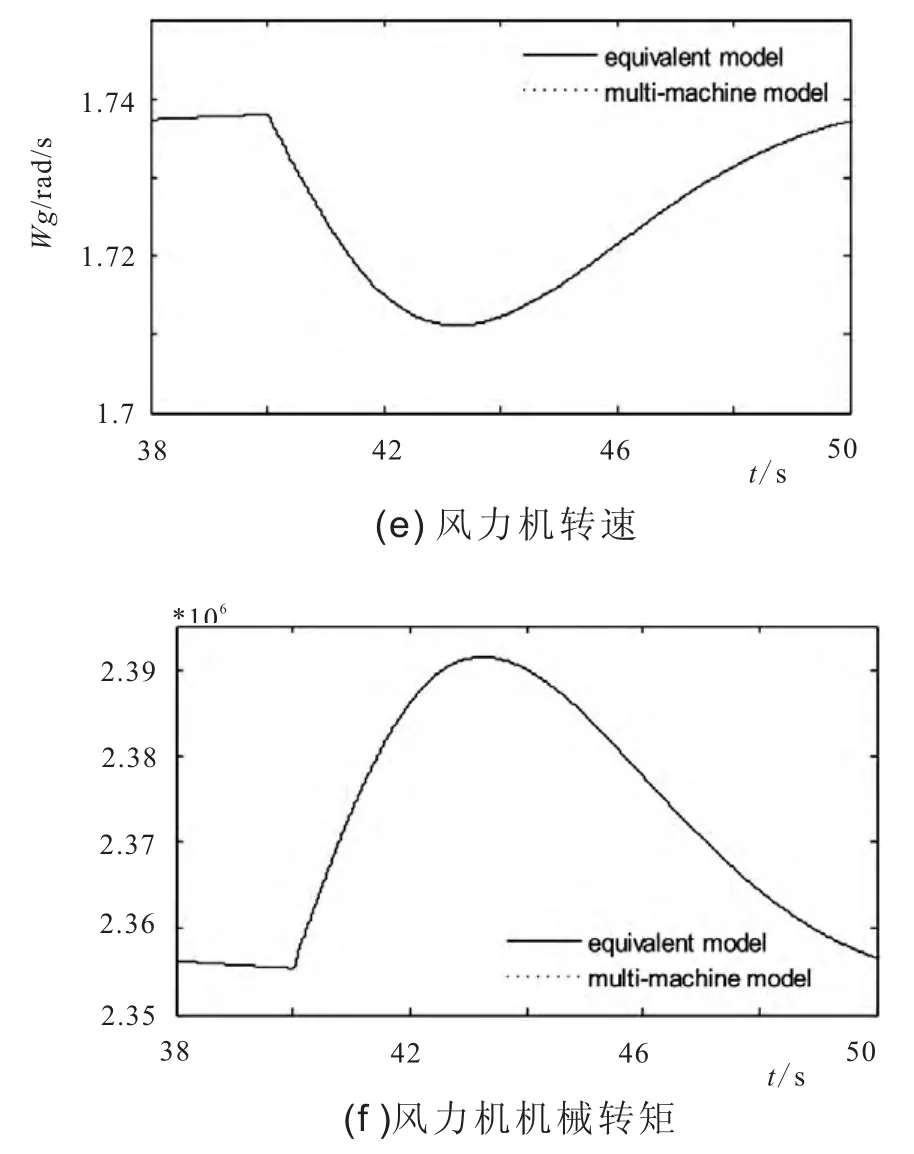
图8 负荷扰动下聚合等值模型校验

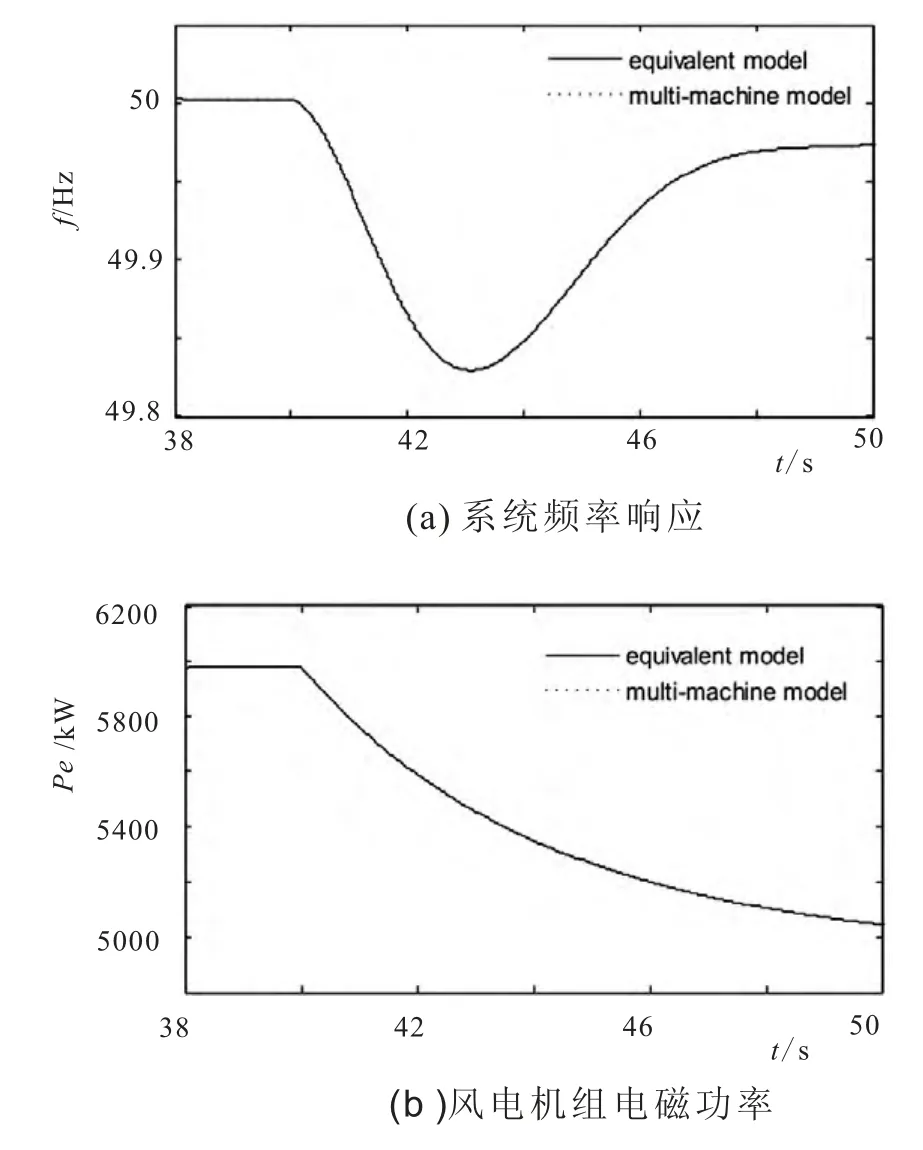
在图6和图7中，实线为聚合等值模型典型系统变量响应曲线，虚线为同风速区三机并网简化模型典型系统变量响应曲线。从图中可以看出，两条曲线完全重合。在负荷和风速两种扰动情况下，通过与三机并网简化模型的对比校验，验证了同风速区机组聚合等值模型的有效性。

图7 风速扰动下聚合等值模型校验

4 结语

本文分析了直驱式风电并网系统结构，在此基础上，考虑风速分布特性和风电场参与系统调频控制策略的研究目的，提出了一种风电场简化建模方法，得出如下结论。1）风电场并网系统中的永磁同步发电机、全功率变流器电磁暂态过程时间尺度很小，对虚拟惯量控制的影响可不计。2）按代表风速分群、同群机组聚合的风电场等值思路可有效反映机组分布特性和实际风场的运行状态。3）本文提出的风电场简化建模方法在保证有功功率平衡的前提下对复杂的永磁同步发电机和全功率并网变流器进行了简化，原理清晰，实现简单，适用于风电场多机频率响应协同控制，仿真校验显示了该建模方法的有效性.

[1]Monica Chinchilla,Santiago Arnaltes,Juan Carlos Burgos.Control of permanent-magnet generators applied to variable-speed wind-energy systems connected to the grid [J].IEEE Transactions on Energy Conversion,2006,21(1): 130-135.

[2]刘巨，姚伟，文劲宇，等.大规模风电参与系统频率调整的技术展望[J].电网技术，2014,38(3):638-646.

[3]尹明，李庚银，张建成，等，直驱式永磁同步风力发电机组建模及其控制策略[J].电网技术，2007,31（15）:61-65.

[4]游敏，吴建军．我国风电发展存在的主要问题—风力发电可持续发展机制研究（上）[R]．2010.

[5]陈杰.变速定桨风力发电系统控制技术研究[D].南京：南京航空航天大学，2011.

[6]El-Sharkawi.Dynamic equivalent models for wind power plants.2011 PES General Meeting，Detroit，2011,(7):24-29.

[7]叶键民.基于特性融合方法的双馈型风机风电场等值建模研究[D].北京:清华大学,2013.

[8]魏巍，王渝红，李兴源，等.基于PSASP的双馈风电场建模及接入电网仿真[J].电力自动化设备，2009,29(12):68-73.

[9]Shi Qiao-ming，Wang Gang，Fu Lijun，et al.State-space averaging model of wind turbine with PMSG and its virtual inertia control[C].39th Annual Conference of the IEEE Industrial Electronics Society，November 10-13，2013，Vienna，Austrial:1880-1886.

[10]李程昊，王李东，林卫星，等.并网变速恒频风力发电系统动态仿真建模及控制[J].电力科学与技术学报，2013,2 8(3):5-15.

[11]陈明亮，肖飞，王颢雄，等．直驱型永磁同步风力发电机无传感器控制[J].电机与控制学报，2009，13(6):792-797.

[12]王刚，侍乔明，付立军，等.虚拟惯量控制方式下永磁风力发电机组轴系扭振机理分析[J].电机与控制学报，2014,18(8):8-16.

[13]耿华,许德伟,吴斌,等.永磁直驱变速风电系统的控制及稳定性分析[J].中国电机工程学报，2009,29(33):68-75.

[14]李和明,张祥宇,王毅，等.基于功率跟踪优化的双馈风力发电机组虚拟惯性控制技术[J].中国电机工程学报,2012,32(7):32-39.