水平井干扰试井模型求解新方法
2015-01-04王小鲁贾永禄王本成王少飞聂仁仕
王小鲁,贾永禄,王本成,王少飞,聂仁仕
(1.油气藏地质及开发工程国家重点实验室(西南石油大学),成都610500;2.青海油田 天然气开发公司,青海 格尔木816000;3.中国石化 西南油气分公司 博士后科研工作站、勘探开发研究院,成都610041;4.中国石油 长庆油田分公司,西安710000)
随着油气藏的开发,动静态结合的多井系统油田开发的试井过程中,后期试井资料受邻井干扰的现象日趋增加[1]。然而,国内外所应用的试井分析方法和解释软件大多是基于单井系统的试井解释模型,忽略了邻井干扰的影响,难以得到正确的分析结果。
干扰试井是多井试井中历史最长的一种方式,Theis率先给出了在均质无限大油藏中由其他点流速变化引起的压力变化的解[2,3]。Tongpenyai提出了考虑激动井表皮效应和井筒储存效应的均质油藏干扰试井模型[4]。Ogbe等进一步给出了注采井同时存在的均质多井油藏中的一口生产井的压力恢复分析理论,并建立了一口注水井的压力降落分析方法[5]。张秀华等研究了考虑井筒储集和表皮系数影响的复合油藏干扰试井模型,并绘制了相应的样板曲线[6]。张德志等研究了三重介质油藏干扰试井压力动态变化,并分析了井筒储存、表皮系数、窜流系数以及弹性储容比对观测井井底压力的影响[7]。谢林峰等利用数值模拟的方法开展了气藏水平井干扰试井参数敏感性研究,定性地揭示了这些参数或参数组合与干扰压力的关系,但不能用于干扰试井解释与评价[8]。
目前国内外许多文献[9-14]对干扰试井问题作了一定的论述,建立了相应的理论模型和数学模型,部分还作出了相应的理论曲线,在油田中的应用也比较普遍;但大都针对直井模型,水平井模型研究甚少。针对试井模型求解方法而言,大都采用Laplace变换求解[15]。本文采用一种新的水平井试井求解方法,获得了三维实空间任意一点的压力精确解,利用新研究的水平井干扰试井分析模型和试井曲线,有效地确定地层的连通情况以及准确获取地层动态参数信息,为油田高效开发提供保障。
1 物理模型
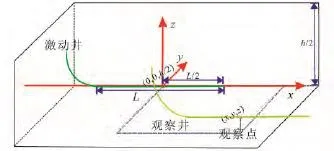
图1 水平井干扰试井渗流模型示意图Fig.1 Schematic diagram of the physical model of the horizontal well interference testing
无限大均质油藏中,考虑两水平井A和B,A为观测井,B为激动井,其渗流物理模型如图1所示。且基于如下物理模型假设:(1)油藏厚度为h,水平井距油藏底面距离为Zw,水平井长度为L;(2)油藏均质且各向异性,水平等厚,顶面和底面为封闭边界,外边界为无限大;(3)激动井开井前整个油藏保持均一的原始压力pi;(4)地层岩石和流体均微可压缩,且压缩系数为常数,原油黏度不变;(5)忽略重力、毛管力的影响,流体在地层中作达西流动。
2 数学模型
在三维笛卡尔坐标系下,多段压裂水平井渗流控制微分方程为

若将井作为点源列入方程,式(1)可改写为

初始条件

外边界条件

底面封闭
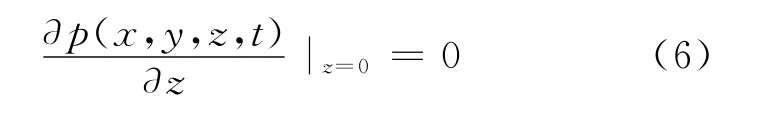
顶面封闭
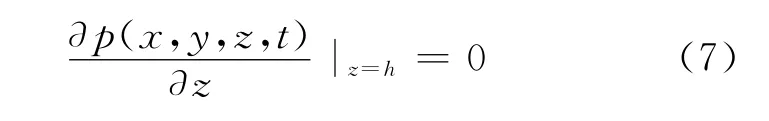
3 无因次数学模型
无因次定义如下
无因次压力

无因次时间
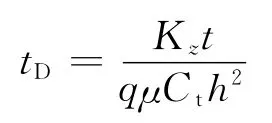
无因次流量

无因次距离
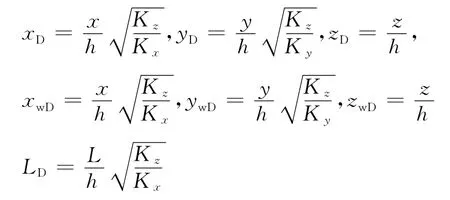
在三维笛卡尔坐标系下,水平井无因次点源渗流控制微分方程为
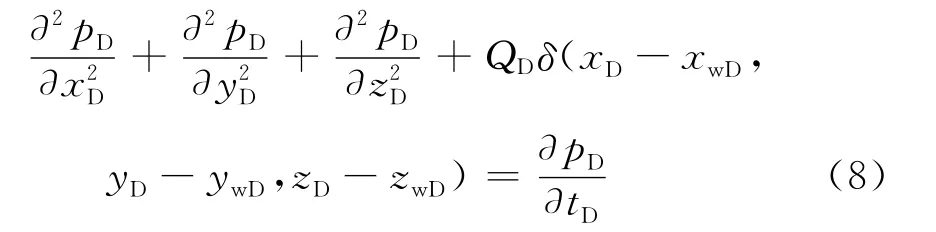
初始条件
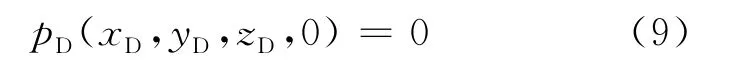
外边界条件
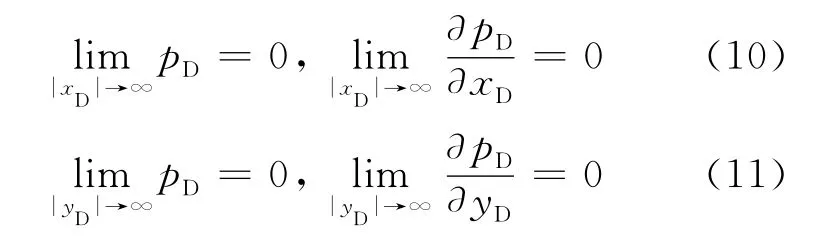
底面封闭
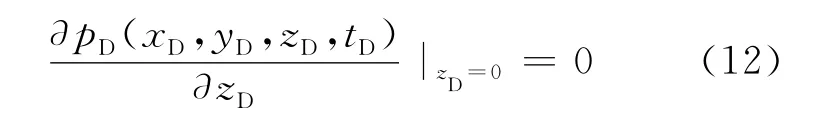
顶面封闭

4 数学模型求解
根据水平井无因次点源渗流控制微分方程和边界条件(式(8)-式(13))的特征,该数学问题为偏微分方程组的初边值问题。本文利用正交变换,将此问题转化为常微分方程的初值问题,再根据矩阵微分方程的基础理论便可以求出本问题的精确解。本文考虑的三维特征值问题如下
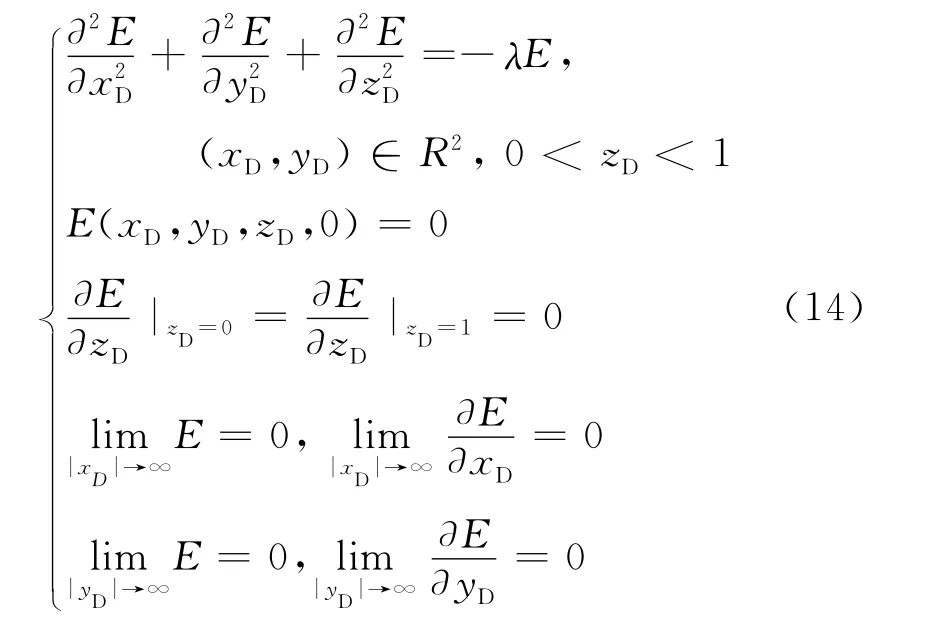
求解式(14)的三维特征值λ和特征函数,首先需分别解出x,y和z方向的3个一维特征值方程
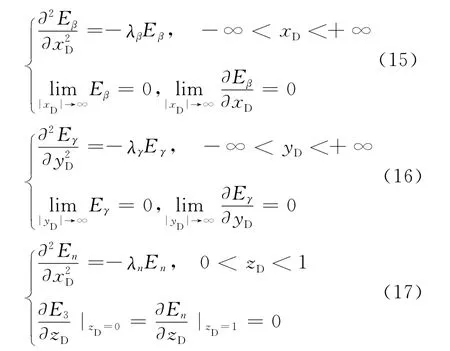
解出特征值和特征函数为
x方向:特征值为λβ=β2,对应的特征函数为Eβ(x)=eiβx,β∈(-∞,+∞);
y方向:特征值为λγ=γ2,对应的特征函数为Eγ(y)=eiγy,γ∈(-∞,+∞);
z方向:特征值为λn=(nπ)2,对应的特征函数为En(z)=cosnπzD,(n=0,1,2,…)。
因此,上述三维特征值λ和特征函数分别为
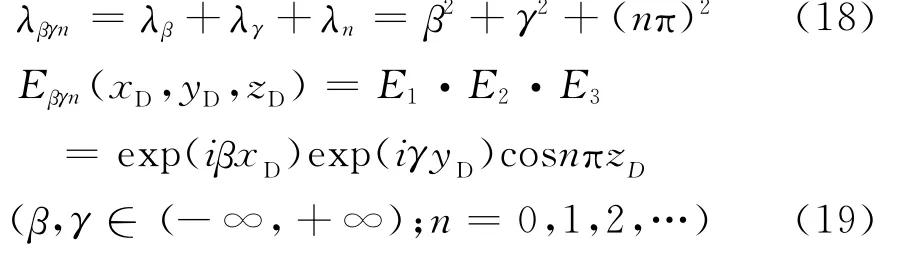
特征函数系:Λ= {Eβγn(xD,yD,zD),(β,γ∈(-∞,+∞);n=0,1,2,…)},构成了三维空间上的完备正交系,则
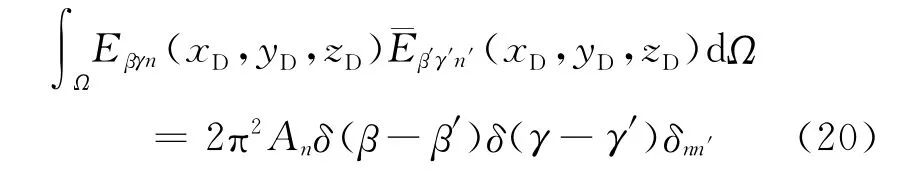
式中

利用特征函数系的完备正交性便可引入相应的正交变换。
首先引入正交变换的定义
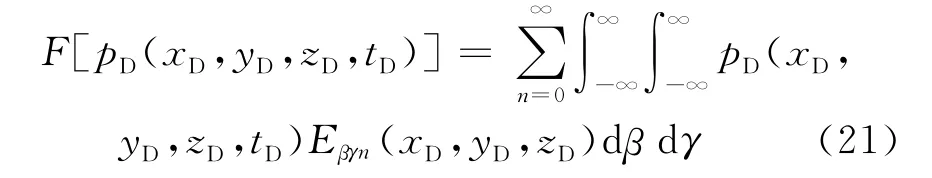
式(21)为pD(xD,yD,zD,tD)的正交变换,记为
如果右端的广义积分是收敛的,那么根据式(20)就可以得到逆变换公式
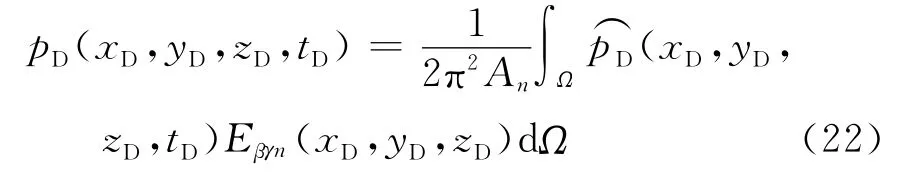
对式(8)—式(13)进行正交变换,最后整理化简得到下面的常微分方程组

解得

代入逆变换公式(22),得到水平井井底压力的无因次精确解,即全空间Ω的点源解
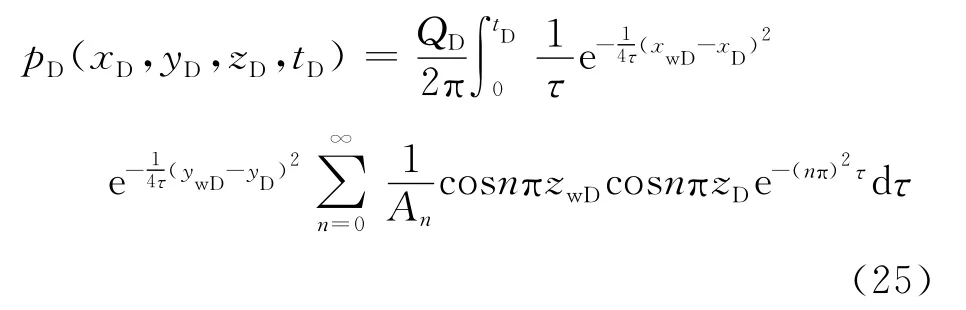
因此,考虑整个机动水平井对观察点(xD,yD,zD)的压力影响,我们则需将所求得的点源解进行扩展到整个水平井,即对点源解(式(25))进行线积分,则观察点的压力表达式为
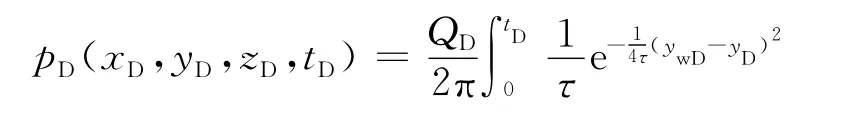
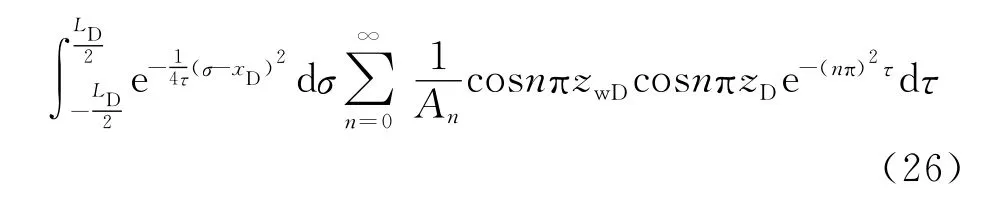
5 样板曲线
图2为激动井和观察井均为水平井的干扰试井井底压力双对数样板曲线。从图中可以看出,激动井忽略井筒储集与表皮效应的影响,其双对数曲线主要可以分为3个流动阶段:早期径向流、中期线性流和晚期径向流。由于激动井早期径向流阶段发生在近井筒地带,且时间较短,因此,对应的观察井主要反映为2个流动阶段:线性流和径向流,出现的时间均晚于激动井。

图2 水平井干扰试井理论样板曲线Fig.2 The type curves of the well test theory for the horizontal well interference testing
6 敏感性分析
图3与图4为观察井位置(x方向和y方向)对井底压力动态样板曲线的影响。从图中可以看出,观察井位置与激动井位置越近,观察井井底压力受激动井干扰越早出现,且观察井的位置变化只影响压力和压力导数曲线的前期,不影响压力导数的后期,即后期径向流压力导数值不变。

图3 观察井x方向距离对试井样板曲线的影响Fig.3 Effect of the distance for observation well in xdirection on the type curves of horizontal well interference testing

图4 观察井y方向距离对干扰试井样板曲线的影响Fig.4 Effect of the distance of the observation well in ydirection on the type curves of the horizontal well interference testing
图5、图6和图7为观察井和激动井不同的堆叠方式对干扰试井曲线的影响。对比3种堆叠方式,激动井的曲线没有变化,均没反映出干扰的特征,而图6观察井双对数曲线比图5和图7更早出现线性流阶段,并且压力导数曲线线性流段的斜率更小。图5与图7表现出“水平并排”和“水平直线并排”这两种堆叠方式对观察井的双对数曲线影响不大,其样板曲线变化趋势一致。
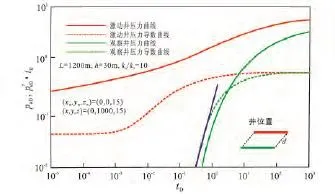
图5 观察井与激动井水平并排干扰试井样板曲线Fig.5 The type curves of the horizontal wells in the interference testing at the same horizontal level
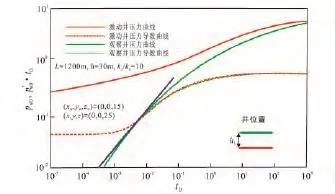
图6 观察井与激动井上下垂直并排干扰试井样板曲线Fig.6 The type curves of the stacked laterals horizontal wells in the interference testing
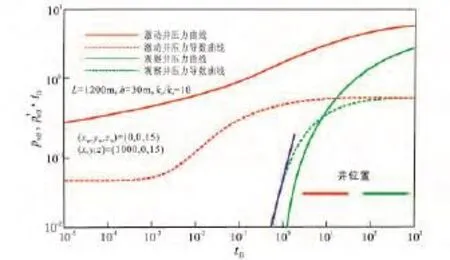
图7 观察井与激动井水平直线并排干扰试井样板曲线Fig.7 The typical curves of the horizontal opposing dual laterals horizontal wells in interference testing
7 结论
a.建立了水平井干扰试井渗流模型,并利用现代数学分析方法进行了求解,获得了三维实空间下任意一点压力的精确解,以及新型的水平井干扰试井样板曲线。
b.获得了水平井干扰试井中观察井的2个典型的流动特征:线性流和径向流,且出现时间均晚与激动井。
c.分析并获得了观察井位置以及堆叠方式对试井样板曲线的影响规律:观察井离激动井越近,双对数曲线线性流出现的时间越早;堆叠方式不同,双对数曲线线性流出现的时间以及斜率均不相同。
符号说明
Ct为综合压缩系数(MPa-1);E()为特征函数;F()为正交变换;h为油层厚度(m);Kx,Ky,Kz分别为x,y,z方向的渗透率;L为水平井长度(m);LD为无因次水平井长度;p为压力(MPa);pi为原始地层压力(MPa);pw为井底压力(MPa);pD为无因次压力;pwD为无因次井底压力;~Q为点源产量(m3/d);Q为总产量(m3/d);QD为无因次产量;rw为井半径(m);t为时间(h);tD为无因次时间;x,y,z为三维空间坐标(m);xw,yw,zw为三维空间点源坐标(m);δ()为δ函数;ξx,ξy和ξz分别为δ函数在x,y,z方向上的函数变量;η为黏度(MPa·s);q为孔隙度;λβ,λγ,λn分别为x,y,z方向特征值;λβγn为三维特征值;An为中间代换变量;τ和σ均为积分变量。
[1]邓英尔,刘树根,麻翠杰.井间连通性的综合分析方法[J].断块油气田,2004,10(5):50-53.Deng Y E,Liu S G,Ma C J.Aggregate analysis method of continuity of formation between wells[J].Fault-Block Oil & Gas Field,2004,10(5):50-53.(In Chinese)
[2]Morris E E,Tracy G W.Determination of pore volume in a naturally fractured reservoir[C]// SPE 1185.Paper presented at Fall Meeting of the Society of Petroleum Engineers of AIME held in Colorado,Denver,1965.
[3]Jargo J R.Effect of well bore storage and wellbore damage at the active well on interference test analysis[J].Journal of Petroleum Technology,1976:28(8):51-58.
[4]Tongpenyai Y,Raghavan R.The effect of wellbore storage and skin on interference test data[J].Journal of Petroleum Technology,1981,33(1):151-160.
[5]Ogbe D O,Brigham W E.A correlation for interference testing with wellbore-storage and skin effects[J].SPE Formation Evaluation,1989,4(3):391-396.
[6]张秀华,贾永禄,刘平,等.考虑井储和表皮的复合油藏干扰试井分析[J].西南石油学院学报,2005,27(1):57-63.Zhang X H,Jia Y L,Liu P,etal.Composite reservoir interference well testing considering wellbore storage and skin factor[J].Journal of Southwest Petroleum Institute,2005,27(1):57-63.(In Chinese)
[7]张德志,王子胜,姚军.三重介质油藏干扰试井压力动态特征[J].油气地质与采收率,2006,13(1):74-76.Zhang D Z,Wang Z S,Yao J.Pressure behavior character of interference well test in tri-media oil reservoir[J].Petroleum Geology and Recvery Efficiency,2006,13(1):74-76.(In Chinese)
[8]谢林峰,甘柏松.气藏水平井干扰试井参数敏感性研究[J].石油天然气学报,2012,34(9):117-120.Xie L F,Gan B S.Parameter sensitivities analysis for horizontal well interference testing in gas reservoirs[J].Journal of Oil and Gas Technology,2012,34(9):117-120.(In Chinese)
[9]Kamal M M,Hegeman P S.New developments in multiple-well testing[J].SPE formation evaluation,1988,3(1):159-168.
[10]高承泰.串漏垂向干扰试井的特征及解释方法[J].石油学报,1994,15(2):65-75.Gao C T.The features and interpretation of vertical interference well testing with serial leakage[J].Acta Pertolei Sinica,1994,15(2):65-75.(In Chinese)
[11]董明,席裕庚.基于遗传算法的干扰试井解释方法[J].石油大学学报:自然科学版,1997,21(4):33-36.Dong M,Xi Y G.A new method of pressure analysis for interference test based on the genetic algorithm[J].Journal of the University of Petroleum,1997,21(4):33-36.(In Chinese)
[12]张继芬,卫秀芬,贾莉卿.确定夹层稳定性垂向干扰试井方法[J].石油学报,1999,20(2):62-66.Zhang J F,Wei X F,Jia L Q.A vertical in terference test method recognizing an unstable impermeable interlayer in multi-layer reservoir[J].Acta Pertolei Sinica,1999,20(2):62-66.(In Chinese)
[13]张同义,杨永智,杜鹃.多井试井资料在油田开发中的应用[J].测井技术,2004,28(B02):65-68.Zhang T Y,Yang Y Z,Du J.Applications of multiwell test data in oil field developments[J].Well Logging Technology,2004,28(B02):65-68.(In Chinese)
[14]刘启国,陈彦丽,张烈辉,等.不关井干扰试井模型和解释方法研究[J].油气井测试,2006,15(1):10-12.Liu Q G,Chen Y L,Zhang L H,etal.Study for disturbing test model with the well opening and its interpreting method[J].Well Testing,2006,15(1):10-12.(In Chinese)
[15]王本成,石国新,路建国,等.考虑二次梯度的非线性双重介质渗流模型[J].成都理工大学学报:自然科学版,2011,38(2):140-146 Wang B C,Shi G X,Lu J G,etal.Study on quadratic pressure gradient terms of the nonlinear filtering flow model in a dual medium reservoir[J].Journal of Chengdu University of Technology(Science & Technology Edition),2011,38(2):140-146.(In Chinese)
