一种新的有限时间收敛的末制导律设计*

李磊，郭建国，周军，王国庆

（1.西北工业大学精确制导与控制研究所，西安710072；2.中国运载火箭技术研究院研究发展中心，北京100076）

一种新的有限时间收敛的末制导律设计*

李磊1，郭建国1，周军1，王国庆2

（1.西北工业大学精确制导与控制研究所，西安710072；2.中国运载火箭技术研究院研究发展中心，北京100076）

针对机动目标的三维拦截问题，提出了一种基于有限时间收敛的新型末制导律设计方法。首先针对三维弹目相对运动学模型，提出了末制导律设计的基本设计原则和要求。其次，提出了一种新的非线性积分型Terminal滑模面，避免了传统Terminal滑模的奇异问题。并针对弹目相对学模型，设计一种具有鲁棒性的积分型Terminal滑模制导律，同时基于李亚普诺夫稳定性理论严格证明了在该制导律作用下，不仅可以达到零化弹目视线角速率的要求，而且也保证了末制导系统在有限时间的稳定性。最后通过对目标机动的拦截仿真，与比例导引律相比，不仅具有更高制导精度，而且也实现了制导系统有限时间的稳定。

制导律，有限时间收敛，Terminal滑模，视线角速率

0 引言

传统的比例制导律是以目标不机动和导弹自动驾驶仪无延迟且无控制约束情况下所得到的一种最优制导律，而随着当前各种高空高速大机动飞行器的出现与发展，传统的比例制导律的制导性能无法获得满意制导效果［1］。

由于滑动模态对于内部摄动和外界干扰具有很强的鲁棒性，因此，对于滑模变结构制导律的研究已经取得了大量成果［2-4］。文献［2］是基于零化视线角速率的思想，设计了滑模制导律。而文献［3］则是基于零化脱靶量的要求来设计变结构制导律。但以上两类思想设计制导律的方法均建立在传统李亚普诺夫渐近稳定性理论基础上，数学原理上只能保证当时间趋向于无穷大时，相应制导系统的状态趋向于零，文献［4-6］探讨了有限时间收敛的变结构制导律。文献［5-6］均采用含有状态分数幂次的Terminal滑模，设计滑模变结构制导律。由于含有状态分数（小于1）幂次的Terminal滑模一般情况下具有奇异问题［7］，因此，所设计的滑模必须解决该问题，这样影响到滑模收敛的性能［8］。

为了能够保证制导系统在有限时间的性能，本文提出了一种新的积分型Terminal滑模，设计了非线性鲁棒末制导律，并严格证明了末制导系统能够零化弹目视线角速率，并实现了有限时间的稳定性。最后数字仿真验证了制导律的有效性。

1 三维末端弹目相对运动模型

针对如图1所示的弹目相对运动关系，根据文献［9］，在视线坐标系下，得到三维末端弹目相对运动学模型为：

图1 三维拦截几何图

其中R为弹目相对运动距离，a，θ分别为两个视线角，ami与ati（i=x,y,z）分别为导弹和目标在视线坐标系上的加速度分量。

由文献［9］可知，描述三维末端拦截问题的弹目相对运动模型就是后两个方程。针对该模型，末制导律设计的基本设计原则和要求为：

（1）弹道要尽可能平滑，由制导系统的准平行接近原理可知，在导弹拦截的末制导段，要以零化弹目视线角速率为原则；

（2）由于末制导段飞行时间有限，所以整个末制导系统的稳定性应该是有限稳定。

针对以上两个基本设计原则和要求，本文提出了新型的Terminal滑模制导律。

2 有限时间收敛的末制导律设计

为了能够设计得到有限时间收敛的末制导律，这里提出一种新的积分型Terminal滑模面，并基于该滑模来设计具有鲁棒性的非线性末制导律。

2.1 新型的Terminal滑模

提出一种新的积分型Terminal滑模为式中l=q/p，q，p均为奇数，且q＞p，a＞0，b＞0的常数。当s=0，可得

为了证明系统（2）是有限时间稳定的，先引入以下引理：

引理1［10］：考虑系统=（fx），（f0）=0，x∊Rn，其中（f·）：Rn→Rn是一个连续函数。假定存在一个连续正定函数V（x）：U→R，其中U是一个开领域，且满足，其中c＞0，a∊（0,1），则=（fx）在原点时有限时间稳定，且收敛时间T满足T≤V1-a（V（0））/c（1-α）。

选择正定函数：

则

可由引理1可知系统（2）在有限时间内收敛到原点。由此可知，如果系统状态在滑动模态s=0上，则状态可在有限时间内达到原点，实现有限时间稳定。

2.2 有限时间稳定的非线性末制导律设计

为了便于说明末制导律设计方法，这里主要以纵向平面内弹目相对运动模型为受控对象，并充分考虑末制导律设计的基本设计原则和要求，来完成末制导律的设计。

利用所提出的Terminal滑模设计新的制导律，可得以下定理：

定理1：针对纵向弹目相对运动模型（3），如果末制导律采取如下形式：

其中ε＞δ，则可在有限时间内制导系统（3）的状态收敛到原点，即保证了末制导系统的有限时间稳定，并实现了零化弹目视线角速率的目的。

证明：考虑Terminal滑模（1），可选取a=b=1/R＞0。可得

引入正定函数：

对V求导，得：

其中c=（ε＞δ）/R1/2＞0，由引理1可知，滑动模态s在有限时间收敛到原点。

当s=0，由2.1部分的推导知，状态x是有限时间稳定，因此，末制导系统是有限时间稳定，且实现了零化弹目视线角速率的目的。

根据以上定理1，注意以下几点：

（1）由定理1知，制导律（4）不会出现奇异问题，因此，就避免了原来分数（小于1）幂次Terminal滑模的奇异问题。

（2）所得到该线性制导律（4）是非线性形式，主要由两部分组成，第1部分为比例导引律的形式，而第2部分含有两个符号函数和一个幂次项，是对比例导引的补偿项。

（3）制导律（4）由于含中符号函数而不连续，为此可将饱和函数代替符号函数，从而使其连续化，可得如下的制导律：

（5）侧向平面的制导律可参考以上设计方法获得。

3 数学仿真

下面通过在末制导段拦截大机动目标的数字仿真，来分析和验证本文所设计的有有限时间收敛的末制导律的有效性。

图2～图4分别为导弹采用有限时间稳定的制导律下的视线角速率˙和制导指令ay的变化曲线。从图2和图3可以看出采用本文设计的非线性末制导律（TMGL）可以保证末制导系统在有限时间是稳定的，并能在有限时间内实现零化视线角速率的要求。从图4中可以看到导弹的加速度指令不会发散，因此，不会产生奇异问题。

图2 视线角速率˙变化曲线（TMGL）

图3 视线角速率˙变化曲线(（放大图）（TMGL）

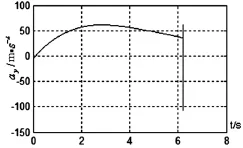
图4 制导指令av变化曲线（TMGL）

图5 视线角速率变化曲线（PN）

图6 制导指令ay变化曲线（PN）

图5和图6分别为导弹采用比例导引律的视线角速率˙和制导指令ay的变化曲线。从图5中明显看到在比例导引律的作用下视线角速率在末端会出现趋向无穷大，而图6中的加速度也会出现激增。最后，采用本文设计的末制导律，其脱靶量为0.77 m，而比例导引律的脱靶量为41.01 m，因此，本文设计有限时间稳定的制导律极大地提高制导系统的制导精度。

4 结束语

本文以拦截导弹攻击大机动目标为背景，对有限时间稳定的末制导律进行研究。首先提出一种基于有限时间稳定的积分型Terminal滑模，其次针对弹目相对运动学模型，基于末制导律的设计原则和要求，设计了具有有限时间稳定和鲁棒性的非线性末制导律。利用Lyapunov稳定理论严格证明了末制导系统的有限时间稳定性，并达到了零化视线角速率的目的。最后，数字仿真也表明了这种新型的非线性制导律使导弹具有对付目标大机动的能力，比起比例导引律，这种制导律不仅可以在有限时间内保证系统稳定，实现零化视线角速率的目的，而且能够获得更好的制导精度。

参考文献：

［1］Babu K R，Sarma I G，Swamy K N，Switch Bias Proportional Navigation for Homing Guidance Against Highly Maneuvering Targets［J］.Journal of Guidance,Control and Dynamics，1994，17（6），1357-1363.

［2］Zhou D，Mu C D，Xu W L.Adaptive Sliding-mode Guidance of a Homing Missile［J］.Journal of Guidance，Control，and Dynamics，1999，22（4），589-594.

［3］郭建国，周凤岐，周军.基于零脱靶量设计的变结构末制导律［J］.宇航学报，2005，26（2）：152-155.

［4］孙胜，周荻.有限时间收敛的变结构导引律［J］.宇航学报，2009，29（4）：1258-1262.

［5］王洪强，方洋旺，伍友利，基于非奇异Terminal滑模的导弹末制导律研究［J］.系统工程与电子技术,2009，31（1）：1391-1394.

［6］崇阳，张科，董蕾.鲁棒全局快速Terminal滑模末制导律研究[J].计算机测量与控制，2013，21（2）：391-393.

［7］Park K B，Tsuji T.Terminal Sliding Mode Control of Second-order Nonlinear UncertainSystem［J］.International Journal of Robust and Nonlinear Control，1999，11（9）：769-780.

［8］Yong F，Yu X H，Man Z H.Nonsingular Terminal Sliding Mode Control of Rigid Manipulator［J］.Automatic,2002，38（12）：2159-2167.

［9］郭建国，周军.基于H∞控制的非线性末制导律设计［J］.航空学报，2009，30（6）：2423-2427.

［10］Bhat S P，Bernstein D S.Finite-time Stability of Continuous Autonomous System［J］.SIAM Journal of Control Optimization，2000，38（3）：751-766.

A New Terminal Guidance Law Design with Finite Time Convergence

LI Lei1，GUO Jian-guo1，ZHOU Jun1，WANG Guo-qing2
（1.Institute of Precision Guidance and Control，Northwestern Polytechnic University，Xi’an 710072，China；
2.R&D Center,China Academy of launch Vehicle Technology,Beijing 100076，China；）

For the case of a three-dimensional interception,a new nonlinear terminal guidance law with finite time convergence is proposed.Firstly，the basic design rules are given according to the mathematic model of three-dimensional relationship between missile and target.Secondly，a new integral sliding mode is present to avoid the singular problem of traditional terminal sliding mode.A robust terminal guidance law is designed，zeroing the rate of line-of-sight angle and finite time convergence stability of guidance system are strictly proven by Lyapunov stability theory.Finally an illustrative example is given to show that better precision and finite time convergence stability are obtained under the new guidance law for intercepting the target with maneuver than proportional navigation law.

Guidance law，finite time convergence，terminal sliding mode，rate of line-of-sight angle

TJ765

A

1002-0640（2015）12-0145-04

2014-11-14

2015-01-17

航天科技创新基金资助项目（N14XW0001）

李磊（1977-），男，安徽利辛人，博士研究生。研究方向：飞行器制导、控制与仿真。