前期整车后悬架硬点优化设计

徐龙 舒进 杨万安 郎锡泽 付文奎

（泛亚汽车技术中心有限公司）

前期整车后悬架硬点优化设计

徐龙 舒进 杨万安 郎锡泽 付文奎

（泛亚汽车技术中心有限公司）

在某车型后悬架硬点前期开发中，确定了整车后悬架硬点设计开发以悬架K&C特性作为优化设计工况。基于工程经验和四连杆式悬架特点，选择对悬架K&C特性有较大影响的悬架设计参数，通过对比分析，选用合适的DOE方法、近似模型法和优化算法，实现了整车后悬架硬点的优化设计，提高了整车开发效率。

整车硬点设计是整车架构开发的基础，决定了整车动力学性能的优劣，目前通过优化手段实现早期悬架硬点开发是国际上领先的汽车公司缩短整车开发周期的一个关键手段。因此，本文结合工程实践，介绍了某项目前期开发中整车后悬架硬点的优化设计过程。

1 项目定义和试验设计

1.1 计算工况及变量定义

选择后悬架结构形式为四连杆式悬架，整车后悬架硬点设计开发以悬架K&C特性作为优化设计工况。基于工程经验及四连杆式悬架特点，选择对悬架K&C特性有较大影响的悬架设计参数，包括纵臂衬套连接点、前束杆内外端点、外倾杆内外端点和下控制臂内外端点等。综合分析多辆竞争车型悬架设计数据，并结合悬架设计工程经验及该项目整车架构尺寸空间，定义出所有变量的设计区间，同时按照悬架K&C特性的评价指标定义输出变量，主要包括轮跳转向、轮跳外倾、上跳转向变化率、下跳转向变化率、侧倾转向、侧倾中心高度、侧向力转向、侧向力外倾、侧向力变形和纵向力转向等。总计21个设计变量，10个输出变量。

1.2 多体动力学模型

在多体动力学软件Motionview中分别建立前悬架系统、后悬架系统、转向系统、动力系统、车身模型和轮胎模型等子系统，并装配成整车多体动力学模型。其中，车身简化为一集中质量（其质量为簧载质量），车身转动惯量在没有实测数据的情况下按照SAE标准进行估算；建模需要的硬点坐标、质量和转动惯量等信息，主要从样车三维模型中获取；建模所需的弹性件力学参数，如衬套刚度和阻尼、减振器的外特性曲线，沿用上一代车型数据。整车多体动力学模型如图1所示。

为方便在优化过程中实现硬点数据的优化循环，建模时需要将硬点数据进行参数化，同时建立Motion⁃view与优化软件ISIGHT的联合仿真模型，可以根据优化迭代计算结果自动更新多体动力学模型中的硬点参数信息，并自动保存模型。所建立的联合仿真模型如图2所示。

1.3 试验设计

试验设计主要包括以下几部分：定义DOE矩阵；生成包含所有样本的计算模型；并行计算所有样本点；将所有样本点的计算结果导入数据库，完成试验设计矩阵。

试验设计矩阵的大小主要取决于设计变量的个数和水平数。从优化设计要求角度，需保证后期能够精确建立近似模型的前提下尽可能减少样本数量。为了保证能够建立精确的近似模型，需要试验设计矩阵满足任意变量个数和任意水平数的需求。常用的试验设计方法有正交数组、中心组合设计、拉丁超立方设计和最优拉丁超立方设计等方法。由于最优拉丁超立方设计改进了随机拉丁超立方设计的均匀性，使所有试验点尽量均匀分布在设计空间，具有非常好的空间填充性和均衡性，从而使得因子和响应的拟合更加精确真实[4]。经过分析悬架设计变量的特点，选择最优拉丁超立方法进行试验设计，确定初始样本数量为400组，按照各变量的设计区间构建DOE矩阵，每个输入变量为7个水平，建立各样本的多体动力学分析模型，并行计算获得各个样本状态下的输出指标。设计变量的DOE矩阵如表1所列。

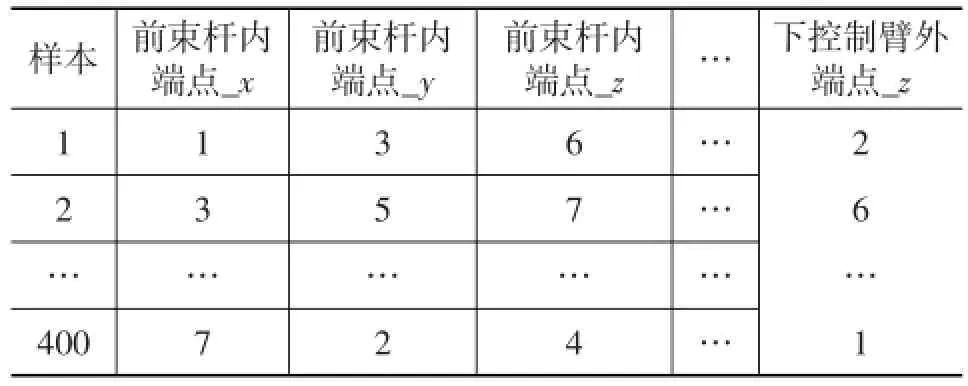
表1 试验设计矩阵

2 近似模型和方差分析

2.1 优化循环的选取

直接优化循环即利用优化工具直接驱动模型产生与提交计算，并通过某种算法对计算结果直接判断，再发出下一步指令。由于受到悬架K&C特性分析中单步分析时间过长的束缚，可能导致直接优化循环时间不可控，从而引入间接优化循环，通过DOE技术建立近似模型，实现对近似模型的优化，最终达到优化实际模型的目的。通过优化近似模型找到最优解，可节省大量的优化时间，但需要对DOE方法与建立近似模型的方法进行具体分析，否则会影响近似模型精度，从而导致优化结果不收敛或错误。

2.2 近似模型

近似模型是通过数学模型的方法逼近一组输入变量和输出变量的方法，使使用者避免高强度仿真计算，减少迭代时间，能预估输入、输出参数之间的响应关系，同时有效避免限于局部最优解，使数值优化算法也有可能找到全局解[5]。本文选择3阶响应面法建立后悬架硬点优化的近似模型[5]。

在建立好近似模型之后必须验证模型精度。验证模型精度通常有误差分析和随机采样点计算对比两种方法。提高近似模型精度的方法主要有在误差较大的区域附近增加DOE样本点和选择精度更高的近似模型[5]两种。图3以侧倾转向和侧向力变形的响应面精度为例说明该近似模型的误差分析，从两图中可以看出，通过响应面近似模型得到的计算结果与通过多体动力学模型得到的结果可以很好地吻合在45°线附近，说明基于样本点的响应面近似模型对整车后悬架K&C性能评价指标的预测精度高，可以满足后续硬点优化的要求。

2.3 方差分析

近似模型生成后，可以通过方差分析得到各设计变量对所有输出变量的贡献量，这有助于提前做出正确的工程判断，尤其是确定对某项性能指标有较大影响力的设计变量。通过分析主效应图，还可以获得输入变量在某个水平时所有试验中输出变量的平均值，因此可以判断当前整个设计输出变量的发展趋势，同时有利于工程开发人员在项目开发前期根据该车型的市场定位确定出恰当的整车后悬架硬点初始值。以侧倾转向和侧向力变形的方差分析结果为例说明，如图4～图7所示。

从图4中可以看出，前束杆内端点的z坐标对侧倾转向的贡献量最大，接近25%，依次为前束杆外端点的z坐标和下控制臂内外端点的z坐标；从图5中可以看出，外倾杆外端点的z坐标对侧向力变形的影响最大，超过25%，依次为外倾杆内端点的z坐标和下控制臂外端点的z坐标。

选择对输出变量贡献量突出的前4个输入变量与其对应的主效应图如图6和图7所示。通过分析侧倾转向的主效应可知，该指标和多个变量基本成线性关系。通过分析侧向力变形的主效应可知，指标和多个变量基本成线性关系，而与外倾杆外端点z坐标存在较强的非线性关系，类似可以得到其他设计输出变量与输入变量的发展趋势，以指导后续设计工作。

3 优化设计

3.1 优化问题定义

通常多目标优化问题可以用以下表达形式描述。

目标函数：

等式约束：

不等式约束：

式中，SFi为规模因子，默认为1；ωi为各整车性能目标的权重系数；为各优化目标的迭代计算结果；为各优化目标的最优期望值；为各约束的迭代计算结果；UB、LB分别为各约束的上、下限。

整车后悬架硬点优化属于有约束优化问题，其优化问题需要在整个设计空间中寻求最优解决方案，为全局优化问题。整车后悬架硬点优化设计的最终目标是在所有变量的设计区间范围内，同时满足悬架K&C性能相关指标的期望值，实现整车操纵性和舒适性的有效平衡。

3.2 优化计算

选择遗传算法进行优化设计。对于遗传算法，扩大每一代的个体数量会比增加代数能够获得更好的优化结果[7]，为此选择总种群个体数为20，进化10代，交叉概率1.0。经过200次迭代计算，以侧倾转向和侧向力变形的优化历程为例，如图8和图9所示，可以看到优化目标参数值均收敛且收敛至约束范围内，罚函数的收敛过程如图10所示。

在整车硬点优化分析中，基于近似模型的优化预测结果必须通过多体动力学模型进行验证。对于个别误差较大的结果，需要将真值添加到样本中重新生成近似模型再进行优化计算，并经过反复验证，最终获得所有问题的理论最优解。利用优化得到的输入变量重新建立车辆多体动力学模型进行计算，并与优化模型求解结果进行对比，如表2所列。

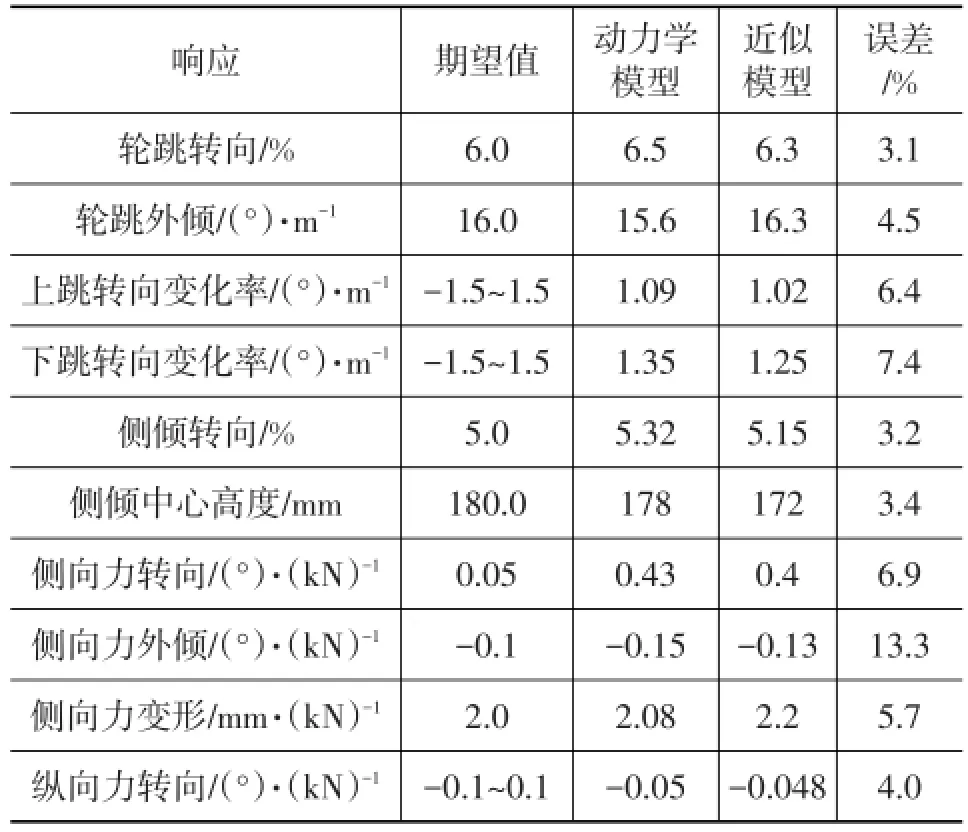
表2 响应优化预测结果误差对比

从各响应的优化过程和误差分析表中可以看出，在本文所确定的后悬架控制变量带宽约束条件下，该最优解能较大程度上满足整车的既定设计目标，并能在各目标期望值之间找到平衡点。

1 John A.Carriere,David T.DeCarteret.Vehicle Handing Pa⁃rameter Trends.SAE2011-01-0969,2011.

2 耶尔森.莱姆帕尔著，张洪欣、余卓平译.汽车底盘基础.上海：科学普及出版社，1992.

3 J.Stuart hunter,William g.hunter.Statistics for Experiment⁃ers:Design,Innovation and Discovery,2ndedition.Wiley-In⁃ter science,2005.

4 Jin Ruichen，Chen Wei．An Efficient Algorithm for Con⁃structing Optimal Design of Computer Experiments．Inte⁃grated Design Automation Laboratory Northwestern Univer⁃sity，2003．

5 Zhang Y.et al Robust Optimal Design for Enhancing Vehicle Handling Performance.SAE 2008-01-0600.

6 Ingber L．Adaptive Simulated Annealing(ASA)：Lessons learned．Journal of Control and Cybernetics，1996，25（1）：33～54．

7 Kalyanmoy Deb，Amrit Pratap，Sameer Agarwal，et a1．A Fast and Elitist Multi objective Genetic Algorithm：NSGA—II．IEEE Transactions on Evolutionary Computation，2002，6（2）．

（责任编辑帘 青）

修改稿收到日期为2015年8月1日。

Optimal Design of Rear Suspension Hard Point in Advanced Vehicle Development

Xu Long,Shu Jin,Yang Wan’an,Lang Xize,Fu Wenkui
（Pan Asia Technical Automotive Center Co.,Ltd）

In the advanced development of a vehicle rear suspension,suspension K&C characteristic is defined as optimal design conditions for vehicle rear suspension hard point design and development.Based on engineering experience and features of four-link type suspension,suspension design parameters which have substantial influence on suspension K&C characteristic are chosen.By comparison and analysis,appropriate DOE approach,approximation model method and optimization algorithm are chosen for rear suspension hard point optimization,which improve the vehicle development efficiency.

Rear Suspension Hard Point，DOE Analysis，Approximation Model，Optimization

后悬架硬点 DOE分析 近似模型 优化

U463.33

A

1000-3703（2015）10-0011-04