基于影响簇选择模型和MCMC采样的社交圈子识别算法
2015-01-03黄佳鑫郭红郭昆
黄佳鑫,郭红,郭昆
(福州大学数学与计算机科学学院,福建福州 350116)
0 引言
社交网络(social networks)起源于网络交友,用户通过社交网络来组织、维护现有的社会关系,并发现新的社会关系[1].通过社交网站,用户可以及时了解好友的动态,例如:好友最新发布的消息等.但是,随着好友数量的增加,好友信息呈爆炸式增长.为了解决这种“信息过载”问题,一种常见的方法是创建用户的个人社交网络,将用户的好友分类到不同的“社交圈子”.当用户的社交圈子建立后,用户就掌握了主动权,不仅在浏览信息的时候可以进行信息流的分类,在发布消息的时候也可以自主选择让哪些好友看到什么样的信息.
当前,所有主流的社交网站都提供社交圈子的设定功能,例如:Google+的“circles”、Facebook及Twitter的“lists”等.“圈子”这个概念由Google+首次提出,用于让用户将不同类型的好友进行分组,放入不同的社交圈子,从而将不同的内容分享给不同的对象,例如:用户可以将某人放进一个或多个社交圈子里,如“朋友圈”、“家人圈”等.
目前为止,Google+、Facebook和Twitter中仍仅支持手动进行社交圈子分类,不仅耗时,而且当添加新的好友时社交圈子不能自动更新.因此,开展自动化社交圈子识别方法的研究具有重要意义.另外,在现实个人社交网络中,用户的好友往往扮演多重角色,发现个人社交网络中具有重叠性的社交圈子结构具有更加实际的意义.重叠社交圈子识别本质上类似于社交网络的重叠社区发现.目前已提出的主流的重叠社区发现算法共有4类[2].基于派系过滤理论:Palla[3]的 CPM 算法,Evans[4]的 Clique Graph算法,基于极大子团合并的EAGLE[5]算法;基于局部信息的方法:Blonde[6]的层次快速展开算法,基于随机种子扩张的LFM[7]算法,基于极大子团扩张的GCE[8]算法;基于标签传播的方法:基于标签传播的COPRA[9]算法,基于均衡多标签传播的BMLPA[10]算法;基于链接聚类的方法:基于单链接层次聚类的LC[11]算法,基于链接密度聚类的DBLINK[2]算法和基于局部边社区的LLCM[12]算法.
上述的重叠社区发现算法尽管能发现重叠社区,但无标识哪些特征导致社区的产生.针对这些问题,2012年,McAuley[13]等人提出了一种基于概率模型的社交圈子识别算法SCD,该算法不仅能有效地识别重叠社交圈子,同时,对每个社交圈子的特征做出解释.然而,该算法具有较高的时间复杂度,为O(n3),不适用于大规模的个人社交网络的社交圈子识别.针对SCD算法存在的较高时间复杂度问题,McAuley[14]等人在原有概率模型的基础上,引入了马尔科夫蒙特卡洛采样算法(MCMCS),提出了MCMCS_SCD算法,该算法以一定的接受概率进行社交圈子的节点采样,有效地将时间复杂度降低为O(n2).尽管MCMCS_SCD算法时间效率相比于SCD算法有所提高,然而,O(n2)的时间复杂度仍限制其在较大规模的个人社交网络圈子识别的应用,并且MCMCS_SCD算法无考虑节点间亲疏关系对待求节点圈子隶属度的影响,使其精度受损.针对上述问题,本文提出基于影响簇发现模型和节点间紧密度的MCMCS_LCD采样算法,并以此为基础设计基于MCMCS_LCD采样的社交圈子自动识别算法SCD_MCMCS_LCD,以实现准确、高效的个人社交网络中社交圈子的自动识别.
1 MCMCS_SCD算法
MCMCS_SCD算法[14]是一种基于马尔科夫蒙特卡洛采样算法的社交圈子识别算法,由节点类型压缩、圈子节点采样及圈子特征向量优化3部分组成,其核心概念的定义如下:
定义1 设个人社交网络用图G=(V,E)表示,则G的对数似然估计函数定义为
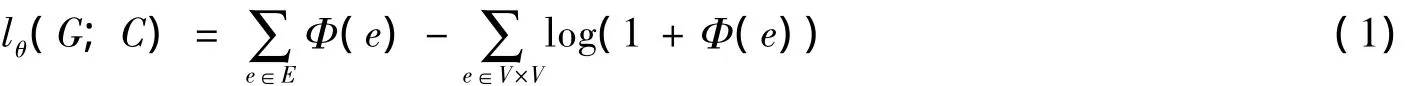
其中:Φ(e)为边e存在于所有圈子的概率之和;C为预测圈子集;θ为圈子特征向量集.
定义2 设有K个社交圈子,F为节点特征个数,P为节点类型集,则最多有2(F+K)种不同的节点类型.显然,还受到节点个数的限制,则=min{2K×,2(F+K)}.
定义3 设两节点构成的边为e,e属于圈子Ck的可能性Eke(1)和不属于Ck的可能性Eke(0)为
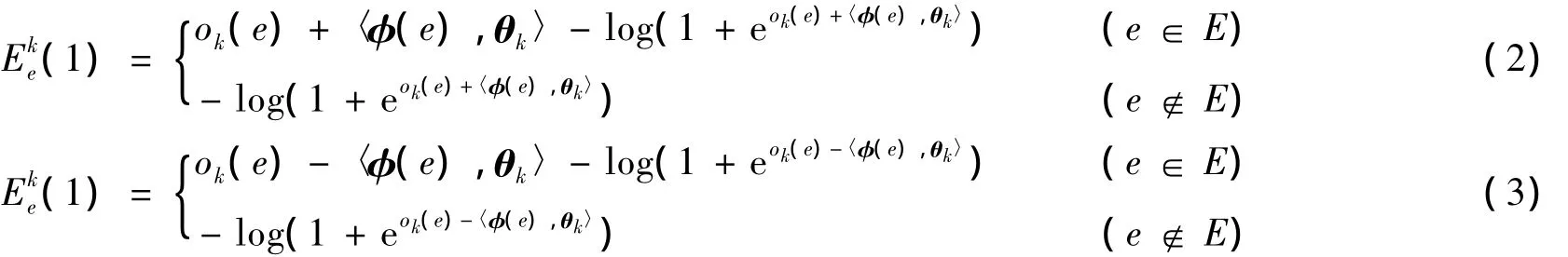
其中:θk为第k个圈子的特征向量;φ(e)为e的特征向量;ok(e)为e属于第k个圈子以外的所有圈子的概率之和.
定义4 设x为待求节点,x属于圈子Ck的可能性lkx(1)和不属于Ck的可能性lkx(0)为

定义5 设S(x)表示节点x所属圈子的情况
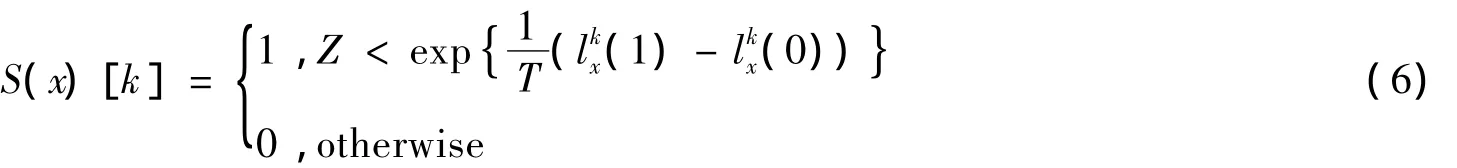
其中:Z服从(0,1)上均匀分布,a(x)=exp((lkx(1)-lkx(0))/T)为节点x的接受概率.
定义6 θk为第k个圈子的特征向量,圈子特征向量的梯度下降优化公式如下:

MCMCS_SCD算法核心思想:给定个人社交网络G,社交圈子的个数K,在节点特征压缩阶段,对网络中节点依据其所属圈子编号和节点特征信息进行节点类型压缩,在社交圈子识别阶段,以一定的接受概率进行社交圈子的节点采样,在圈子特征优化阶段,对每个圈子的特征向量进行梯度下降优化.迭代执行这3个过程,直到式(1)的对数似然函数值达到最大.
MCMCS_SCD算法存在的主要问题:
1)时间复杂度高:节点x的接受概率由P中所有节点决定,在实际个人社交网络中,特征完全相同的节点并不多,则P与V属于同一个数量级,时间复杂度趋近于O(V2).
2)算法将P中所有节点考虑在内,包含了一些关联不大甚至对节点x有消极影响的节点,导致社交圈子划分精度降低.
3)由Eke(1)和Eke(0)计算公式可得,算法仅考虑节点构成边的特征信息,无考虑节点间亲疏关系对待求节点的圈子隶属度的影响,这是不合适的.
举例来说,令x,y,z为网络中的三个节点,x与y,z分别构成边的圈子隶属度都为0.9,但是,节点x与y的紧密度为0.7,而节点x与z的紧密度为0.2,依据算法,忽略节点间紧密度,节点y和节点z决定节点x的圈子隶属度是相同的,显然不够合理.
2 SCD_MCMCS_LCD算法
正如前面分析,MCMCS_SCD算法存在时间复杂度高及使用过多、关系过远的节点决定待求节点社交圈子隶属度的问题.鉴于节点的圈子隶属度应由与节点关联紧密的节点决定,如果能找到这样一个度量函数,该函数值能够反映簇内节点的连接紧密程度,并按算法迭代进行单调改变,直到某时刻到达极值时终止算法,即可求得与节点关联紧密的节点集,进而求得节点的社交圈子隶属度.
定义7 对于每个节点x,其影响簇Hx定义为

其中:SNode为影响节点x社交圈子隶属度的节点集.
MCMCS_SCD算法的节点x的影响簇为P,算法复杂度较高,因此,为了提高以寻找纯度较高的影响簇为手段的社交圈子自动识别算法的效率,探索一种基于局部网络求解的方法.
2.1 节点影响簇发现模型
设LG(G,x)为节点x在G中所处的局部环境,设TN(y,z)为节点y,z在LG(G,x)中的紧密度.若能求出任意两个节点的TN值,就可以根据一定的度量策略在迭代过程中生成节点x的影响簇Hx.这种思路的有效性取决于LG(G,x),TN(y,z)和度量函数选择的有效性.
2.1.1 局部环境和紧密度的定义
社交网络具有复杂网络的小世界性的特点.因此,对于任意节点x,根据小世界网络的六度空间现象,以x为起点,沿着与x有关的边往外逐层扩展,直到形成以x为中心,半径为6的网络,即为x的局部环境LG(G,x),显然,算法并不需要求出LG(G,x)的节点集,只需要在求得与x紧密连接的节点时,判断该节点是否包含于LG(G,x)中.
选择合适的TN(y,z)是算法另一个需要解决的问题.对于任意节点y,z在LG(G,x)中的紧密度,可以有许多不同的计算方法.例如仅根据节点属性或者节点间链接信息来度量节点间的紧密度,前者将节点集看成无关联的对象集,只利用反映节点内源特征的节点属性数据而忽略了节点间的联系,后者则仅考虑节点间链接关系而忽略节点本身所具有的属性[15].单纯地考虑节点属性或链接信息,都可能造成许多可利用信息的遗漏.因此,将节点属性和节点间链接信息进行融合,用融合结果来表示节点间关系的紧密度.采用余弦系数和Jaccard系数,分别根据节点属性信息和节点间链接信息进行节点间紧密度度量,为此,给出紧密度度量公式定义如下:
定义8 对于任意节点y,z,其紧密度TN(y,z)定义为
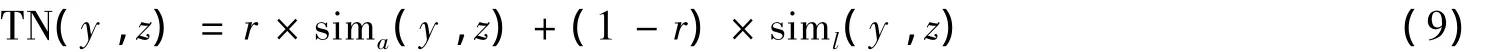
其中:sima(y,z)为余弦系数;siml(y,z)为Jaccard系数;r用于区分节点属性和节点间链接关系对紧密度的贡献,r∈[0,1].
2.1.2 度量函数的选择
如何在LG(G,x)中选择合适的度量函数是算法需要解决的核心问题.参考Clauset[16]提出的局部社团探测的思路,以节点x为起点,通过最大化度量函数为目标来搜索节点的局部社团,其定义与影响簇的定义相符,将其作为节点影响簇的方法是可行的.Clauset采用社团内外链接程度的相对关系来衡量局部社团的局部模块度R为度量函数,并无考虑节点属性信息.综合考虑节点属性信息和节点间链接信息,提出基于紧密度的局部模块度M,并将M作为搜索影响簇的度量函数.
定义9 对于影响簇Hx,局部模块度M定义为

其中:Tin是簇内任意两个节点的紧密度之和;Tout是簇内部与簇外部节点间的紧密度之和.
采用Clauset的局部社团探测算法框架,以上述的基于紧密度的局部模块度M为度量函数,通过最大化局部模块度M为目标求得x的局部社团,即为x的影响簇Hx.
2.2 基于紧密度的社交圈子隶属度
在社交圈子识别阶段,MCMCS_SCD算法无考虑节点间亲疏关系对待求节点的圈子隶属程度的影响.采用前述的紧密度公式作为节点间亲疏关系的度量标准,将紧密度作为隶属度的权值,更准确地判断节点的社交圈子隶属度.
上述例子中,将紧密度作为隶属度权值,则节点y决定节点x的圈子隶属度为0.63,而节点z决定节点x的圈子隶属度为0.18,与事实相符.
考虑节点间紧密度后,公式(4)和公式(5)修改成:

2.3 基于MCMCS_LCD的社交圈子自动识别算法
借鉴MCMCS_SCD算法框架,以上述的影响簇发现模型和紧密度公式为基础,设计实现了基于MCMCS的MCMCS_LCD算法,并进一步设计实现了基于MCMCS_LCD的社交圈子自动识别算法SCD_MCMCS_LCD.算法详细步骤如下.
算法1 SCD_MCMCS_LCD算法
输入:个人社交网络G=(V,E),社交圈子个数K;
1. FOR∀x∈V DO
2. 寻找节点x的影响簇Hx
3.ENDFOR
4.WHILE true
5. FOR i=1to maxIter
6. FOR k∈{1,…,K}DO
7. FOR ∀x∈V DO
8. 设x0为x∉Ck的情况,x1为x∈Ck的情况
9. FOR ∀y∈HxDO
10. IF ∀(x,y)∈E THEN
11. lkx(0):=lkx(0)+TN(x,y)Ek(x,y)∈E(0)
12. lkx(1):=lkx(1)+TN(x,y)Ek(x,y)∈E(1)
13. ELSE
14. lkx(0):=lkx(0)+TN(x,y)Ek(x,y)∉E(0)
15. lkx(1):=lkx(1)+TN(x,y)Ek(x,y)∉E(1)
16. ENDIF
17. ENDFOR
18. Z←μ(0,1)
19. IF Z <exp((lkx(1)-lkx(0))/T)THEN
20. S(x)[k]:=1
21. ELSE
22. S(x)[k]:=0
23. ENDIF
24. ENDFOR
25. ENDFOR
26. ENDFOR
27. θt+1:=argmaxlθ(G;Ct)-λΩ(θ)//L-BFGS优化θ
28. t:=t+1
29.ENDWHILE
步骤1至步骤3的for循环是基于紧密度的局部社团探测算法,在局部环境下,探测任意节点x的影响簇的实现;步骤4至步骤29最外层的while循环反复执行圈子节点采样和圈子特征优化,直到取得最大似然函数值;步骤5至步骤26为圈子节点采样阶段,算法迭代运行,直到达到最大迭代次数;通过步骤9至步骤17求得x的圈子隶属度,进而通过步骤19计算得到x的接收概率a(x);步骤27为圈子特征优化阶段,利用拟牛顿法对圈子特征向量θ进行梯度下降优化.
2.4 算法时间复杂度分析
正如前述分析,SCD_MCMCS_LCD算法由影响簇发现、圈子节点采样及圈子特征向量优化3部分组成.影响簇发现过程,计算任意节点的局部社团为节点影响簇,该过程只需执行一次,时间复杂度为O(×n2×d),n为将要寻找的社团成员数目,d为平均节点度.圈子节点采样过程,节点的接收概率由其影响簇节点计算得到,重复圈子采样过程,直至达到最大迭代次数,该过程时间复杂度为O(D×K××),D为采集次数,为节点平均局部社团成员数.圈子特征向量优化过程,每个圈子的特征向量通过拟牛顿法进行梯度下降优化,时间复杂度为O(W×K××),W为特征优化次数.重复圈子节点采集和圈子特征向量优化过程,直到取得最大对数似然函数值,算法的总时间复杂度为O(J×(×n2×d+(D+W)×K××))~O (×),其中J为圈子识别次数.SCD_MCMCS和SCD_MCMCS_LCD算法时间复杂度主要差别在于影响簇Hx的选择策略上,SCD_MCMCS算法的影响簇采用压缩后的节点类型集P,因此SCD_MCMCS算法的时间复杂度为O(J×(+(D+W)×K××))~O (×),两者的空间复杂度都主要取决于总节点数、影响簇节点数和节点特征数N,算法的空间复杂度分别为 O (×(N+))和 O (×(N+)).
3 实验结果与分析
3.1 实验数据集
实验采用的数据集来自Stanford大学提供的Facebook数据集[14].Facebook数据集包含10个用户的个人社交网络,总共193个圈子和4 039个用户,平均每个用户有19个社交圈子,每个圈子平均有22个好友.采用4个数据量不同的数据集进行实验.
3.2 评价指标
实验采用与文献[14]相同评价指标,分别是圈子划分精度和F1测度来度量算法性能,定义如下.
1)圈子划分精度.设预测圈子集为C={C1…CK},实际圈子集为=…},圈子划分精度计算公式如下:

其中:f函数为预测圈子集与实际圈子集的匹配函数;BER(C,)表示圈子Ck和匹配误差率.
2)F1测度.F1测度计算公式如下:
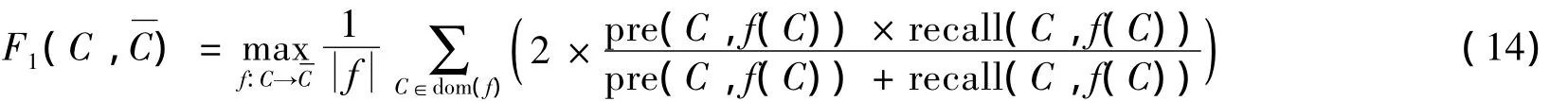
其中:pre(C,f(C))为准确度;recall(C,f(C))为召回率;F1值越大聚类效果越好.
3.3 参数选择
实验中,SCD_MCMCS_LCD和SCD_MCMCS算法的社交圈子识别阶段迭代次数J,圈子节点采集阶段的迭代次数D及圈子特征优化阶段迭代次数W的上限,分别设置为30、50、50进行实验.同时,为了克服随机性对算法测试的影响,所有实验结果均取30次运行结果的平均值.
文献[14]一共提出了4种边特征向量计算方法,实验证明,第一种方法优于其他三种方法,因此,采用第一种边特征向量方法进行实验.算法其它参数均取原作者论文中的推荐值.
3.4 节点影响簇实验结果
在4个数据集上分别应用节点类型压缩算法,得到不同类型节点数,分别应用基于紧密度的局部社团探测算法,取系数r为0.5,得到节点平均局部社团成员数,如表1所示.由表1可知,SCD_MCMCS算法压缩率平均为85%左右,时间复杂度趋向于 O (),而SCD_MCMCS_LCD算法平均局部社团成员数相比于总节点数非常小,约为总节点数的5%~14%,时间复杂度趋向于 O (),从理论分析可得,SCD_MCMCS_LCD相比于SCD_MCMCS算法应具有更高的效率,并且,SCD_MCMCS_LCD算法节点影响簇纯度有较大提高,理论上,SCD_MCMCS_LCD应比SCD_MCMCS算法具有更高的圈子划分精度和F1测度.
为了验证上述关于算法精度、F1测度和时间复杂度的分析,以及验证算法的有效性和通用性,在4个数据集上分别采用SCD_MCMCS、SCD_MCMCS_LCD、CPM和LC算法,取系数r为0.5.
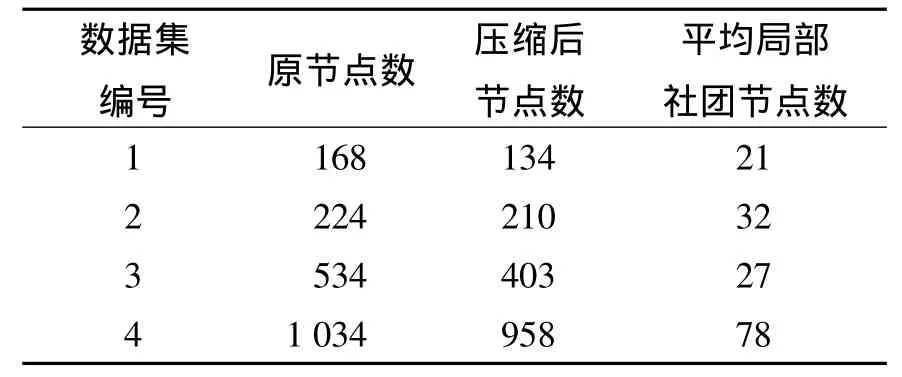
表1 影响簇节点个数Tab.1 Number of node in influential cluster
3.5 运行时间实验结果
图1为不同数据集上,四种算法运行时间,SCD_MCMCS_LCD和SCD_MCMCS取K值为4.由图1可得,SCD_MCMCS_LCD算法在K值相同的情况下,运行时间远小于SCD_MCMCS算法,时间至少减少50%.两者在节点影响簇的选择策略上的巨大差异造成此现象的产生.另外,SCD_MCMCS_LCD算法相比于COPRA和LC算法,具有更高的时间效率.
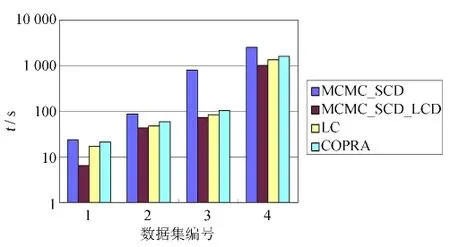
图1 几种算法运行时间比较Fig.1 Time efficiency comparison of various algorithms
3.6 划分精度和F 1测度实验结果
图2、3显示在不同数据集上的四种算法的划分精度和F1测度.

图2 几种算法精度比较Fig.2 Precision comparison of various algorithms

图3 几种算法F1测度比较Fig.3 F1 comparison of various algorithms
由图2、3可得,SCD_MCMCS_LCD的划分精度和F1测度超过SCD_MCMCS算法,这是因为SCD_MCMCS算法忽略不同节点所处网络环境的差异,将节点类型集P作为任意节点的影响簇,将很多关联稀疏甚至有消极影响的节点考虑在内,而SCD_MCMCS_LCD算法引入社交网络中存在的小世界网络的六度空间概念,考虑不同节点所处的相异局部环境,通过局部探测算法搜索与节点关联紧密的局部社团为其影响簇,舍弃了不合格的节点,提高了簇的纯度,进而提高了算法的划分精度和F1测度.并且相比于SCD_MCMCS算法,SCD_MCMCS_LCD算法不仅考虑节点构成的边的特征信息,还考虑节点间紧密度对待求节点圈子隶属度的影响,进一步提高算法的划分精度和F1测度,最终获得更好的圈子划分效果.另外,由图中可得,LC算法具有较低的划分精度和F1测度,这是由于其将所有边都分配到特定的圈子中,造成圈子结构过度重叠,导致较低的划分精度和F1测度.COPRA算法划分精度和F1测度介于SCD_MCMCS_LCD和LC之间.
3.7 圈子特征向量
相比于已有的重叠社区挖掘算法,SCD_MCMCS_LCD算法不仅能识别重叠社交圈子,还能对每个社交圈子的特征进行解释,如图4、5所示.图4、5分别显示了第一个数据集上识别出的两个圈子的特征,A圈子表示相同学校且相同家乡的好友圈子,B圈子表示在相同时间入职于同一家公司,且为校友的好友圈子.
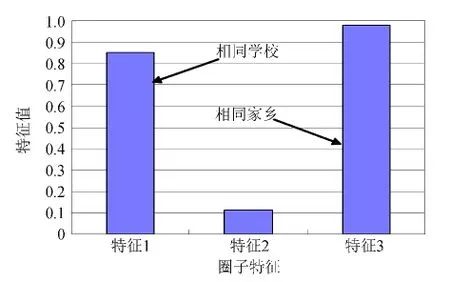
图4 A圈子特征Fig.4 Features of A circle
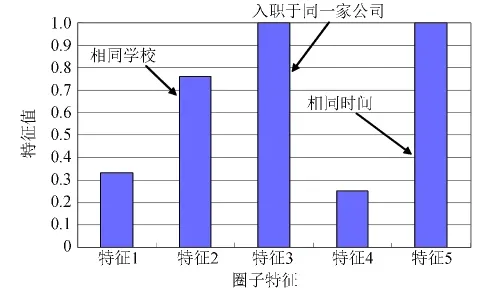
图5 B圈子特征Fig.5 Features of B circle
3.8 系数r实验结果
定义8中,通过系数r区分节点属性和节点间链接关系对紧密度的贡献.采用第1个数据集进行实验,实验结果如表2.由表2可得,基于融合节点属性信息和节点间链接信息的紧密度的SCD_MCMCS_LCD算法,划分精度和F1测度高于仅基于属性信息或者节点链接信息的紧密度的SCD_MCMCS_LCD算法,当r=0.25时,算法划分质量最好.可见,节点属性和节点间链接信息都对圈子识别有着积极的意义,孤立地依靠某一类信息都可能造成一些信息的遗漏,从而影响最终的社交圈子划分效果.

表2 系数r对圈子识别的影响Tab.2 The influence of coefficient r of circle detection
4 结语
目前多数社交网络仍仅支持由用户手动划分其社交圈子,不仅耗时,而且社交圈子无法自动更新.分析SCD_MCMCS算法,指出该算法的三个缺点,并提出基于融合影响簇选择模型和紧密度的MCMCS_LCD的社交圈子自动识别算法SCD_MCMCS_LCD,通过理论分析和实验检验,证明提出的算法在具有较低的时间复杂度和空间复杂度的同时,具有较好的社交圈子识别效果.
接下来,将进一步考虑更多的局部影响簇发现策略,通过比较不同策略的优势,实现更有效的社交圈子识别.同时,通过将算法扩展到有向网络和加权网络,拓展算法的适用范围.
[1]曹怀虎,朱建明,潘耘,等.情景感知的P2P移动社交网络构造及发现算法[J].计算机学报,2012,35(6):1 223-1 234.
[2]朱牧,孟凡荣,周勇.基于链接密度聚类的重叠社区发现算法[J].计算机研究与发展,2013,50(12):2 520-2 530.
[3]Palla G,Derenyi I,Farkas I,et al.Uncovering the overlapping community structure of complex networks in nature and society[J].Nature,2005,435(7 043):814-818.
[4]Evans T S.Clique graphs and overlapping communities[J].Journal of Statistical Mechanics Theory and Experiment,2010,34(3):257-265.
[5]Shen Huawei,Cheng Xueqi,Cai Kai,et al.Detect overlapping and hierarchical community structure in networks[J].Physica A:Statistical Mechanics and its Applications,2009,388(8):1 706 -1 712.
[6]Blondel V D,Guillaume JL,Lambiotte R,et al.Fast unfolding of communities in large networks[J].Journal of Statistical Mechanics:Theory and Experiment,2008,30(2):155 -168.
[7]Lancichinetti A,Fortunato S,Kertész J.Detecting the overlapping and hierarchical community structure in complex networks[J].New Journal of Physics,2009,625(15):19 -44.
[8]Lee C,Reid F,Mcdaid A,et al.Detecting highly overlapping community structure by greedy clique expansion[C]//Proc of the 4th International Workshop on Social Network Mining and Analysis.Washington D C:ACM,2010:33-42.
[9]Gregory S.Finding overlapping communities in networks by label propagation[J].New Journal of Physics,2010,12(10):2 011-2 024.
[10]Wu Zhihao,Lin Youfang,Gregory S,et al.Balanced multi- Label propagation for overlapping community detection in social networks[J].Journal of Computer Science and Technology,2012,27(3):468 -479.
[11]Ahn Y Y,Bagrow J P,Lehmann S.Link communities reveal multi- scale complexity in networks[J].Nature,2010,466(7307):761-764.
[12]潘磊,金杰,王崇骏,等.社会网络中基于局部信息的边社区挖掘[J].电子学报,2012,40(11):2 256-2 263.
[13]McAuley J,Leskovec J.Learning to discover social circles in ego networks[C]//Proc of the 26th Annual Conference on Information Processing Systems.Lake Tahoe:[s.n],2012:548 -556.
[14]McAuley J,Leskovec J.Discovering social circles in ego networks[J].ACM Transactions on Knowledge Discovery from Data,2012,8(1):73-100.
[15]林友芳,王天宇,唐锐,等.一种有效的社会网络社区发现模型和算法[J].计算机研究与发展,2012,49(2):337-345.
[16]Clauset A.Finding local community structure in networks[J].Physical Review E,2005,72(2):254-271.
