基于能量原理与中间主应力效应的新岩石强度准则探讨

牛超颖，贾洪彪，马淑芝，王 康

(中国地质大学(武汉)工程学院,武汉 430074)

基于能量原理与中间主应力效应的新岩石强度准则探讨

牛超颖，贾洪彪，马淑芝，王 康

(中国地质大学(武汉)工程学院,武汉 430074)

能量转化是物质物理过程的本质特征,分析岩石破坏过程中的能量变化规律及其与强度和整体破坏之间的联系,更有利于反映外荷载作用下岩石强度变化与整体破坏的本质特征。从能量耗散与能量释放的角度,基于前人研究成果及中间主应力效应,提出了岩石能量释放基于应力分配的一般形式,并结合最小主应力对能量强度准则进行了分析,提出了新的强度准则。研究表明:运用能量原理研究中间主应力效应是可行的；在最小主应力一定时,能量释放分配系数与岩石极限强度成线性关系,且随着能量释放分配系数的提高,岩石极限强度逐渐降低；新的能量强度准则可以充分考虑中间主应力的影响,从而可以弥补岩石常规破坏判据的不足。

岩石力学；能量强度准则；中间主应力；能量释放分配系数；最小主应力

2015,32(11):93-98

1 研究背景

长期以来,判断工程失效或破坏的依据是以经典弹塑性理论为基础的岩石强度与破坏准则,比如Tresca准则、Mises准则、Griffith准则、Mohr-Coulomb准则、Hoek-Brown准则等。然而,岩石是典型的非均匀介质,常规的应力强度理论与破坏准则大多很难有效地分析岩石这种复杂的强度变化与整体破坏行为。而能量转化是物质物理过程的本质特征,因此,分析岩石破坏过程中的能量变化规律及其与强度和整体破坏之间的联系,将更有利于反映外荷载作用下岩石强度变化与整体破坏的本质特征。近年来,国内外学者开展了不少相关方面的研究,通过能量分析来描述岩石的变形破坏行为,并取得了一定的进展。例如,谢和平院士等[1-2]建立了以能量消耗与能量释放为基础的岩石破坏准则；张后全等[3]在文献[1-2]等的基础上建立了脆性岩石真三轴能量强度准则；高红等[4]建立了适用于岩土类材料的三剪能量屈服准则。除此之外,还有其他一些专家学者也开展了相关研究[5-7]。

但是,目前以能量角度分析岩石力学行为还处于初期阶段,有些问题还需要进行讨论和研究。目前建立的能量准则,主要以能量释放为重要的分析途径,在考虑岩体受力实际状态时,以能量释放量正比于单元中储存的可释放能量,并按与最小压应力的差进行分配,而没能恰当考虑中间主应力对岩石强度的影响。

有关中间主应力对岩石强度影响的研究从20世纪30年代就已经开始[8],特别是随着真三轴试验机的研发[9]和岩石的真三轴试验成果的发表,国内外专家学者越来越认识到中间主应力对岩石极限抗压强度的影响具有一定的规律性,并为此对中间主应力效应进行了深入的研究。日本东京大学教授茂木清夫等[10-11]从20世纪60年代开始,经过长期的研究,成功研制了真三轴压力试验机,并取得了大量试验数据,为中间主应力效应的研究做出了积极的贡献。国内学者张金铸、林天健、高延法、陶振宇、李小春等[12-13]也利用真三轴压力试验机对大冶大理岩、稻田花岗岩、拉西瓦花岗岩等多种岩石进行了一系列的岩石真三轴试验,并对试验成果进行了分析和总结,对中间主应力效应的研究也做出了积极的贡献。

国内外专家学者通过已有的试验数据进行分析得出了一些规律性的结论,但是其内部作用机制的研究还较少见。随着现代化科学技术及基础理论的发展,目前对其进行更为深入的研究提供了可能。由此可以看出,能量准则与中间主应力效应的研究具有相辅相承的特点:中间主应力效应的研究有利于能量准则更趋于符合实际；利用能量机制可以更好地分析中间主应力对岩石强度的影响。因此,本文将二者结合起来进行分析和讨论,研究岩石在外荷载作用下的能量强度准则。

2 基于能量原理的强度准则

近年来,随着现代技术及基础理论的发展,运用能量原理进行研究是各学科新兴的热门领域,在岩石力学方面也涌现出了大量基于能量的岩石力学行为的理论和研究。其中,在岩石的强度准则的研究中,谢和平院士等[1]于2005年提出基于能量耗散与释放的岩石强度准则,其能量耗散与能量释放的思想依据是:随着外部荷载作用下岩体单元损伤程度的加剧,强度逐渐减小,当岩体某一单元的可释放应变能达到该单元所需的破坏表面能时,该单元将发生破坏,以弹性表面能的形式释放。当一定数量的单元在瞬间发生上述破坏时,就形成了岩体的整体破坏。其整体破坏准则为:外力对岩体所做的功,其中一少部分转化为岩体单元的耗散能Ud,使岩体强度逐渐丧失；另一部分转化为逐步增加的可释放应变能Ue。Ue储存并达到岩体单元破坏表面能U0时,应变能Ue释放使岩体单元发生整体破坏。

该强度准则具体的数学表达形式[1]为:

式中:σ1,σ2,σ3分别为岩石所受最大、中间、最小主应力；σc为岩石单轴抗压强度；σt为岩石单轴抗拉强度；μ为岩石泊松比。

张后全等[3]在谢和平院士等[1-2]研究的基础上考虑中间主应力的影响,引入俞茂宏教授的统一强度理论对中间主应力效应的分析,其数学表达式为:

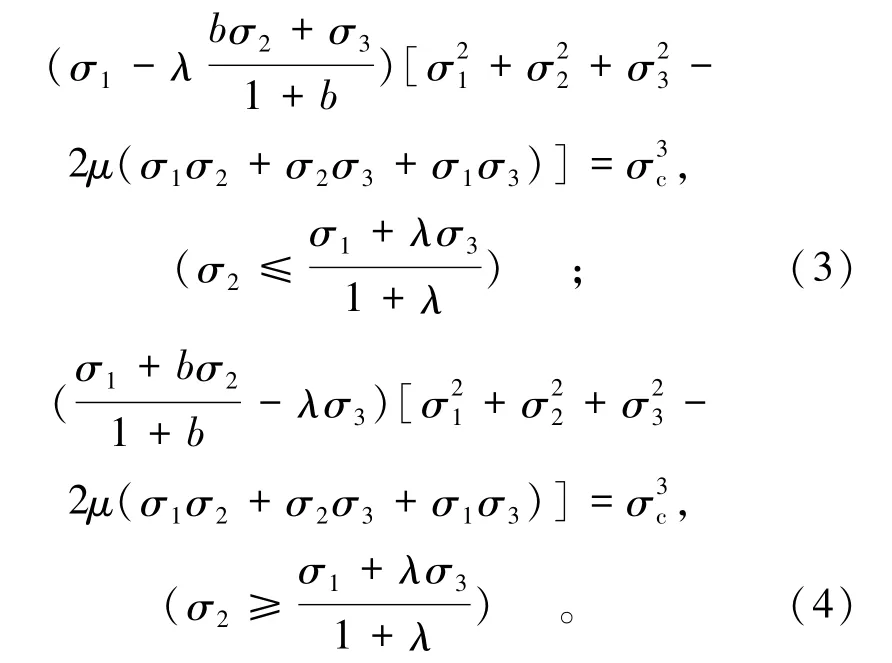
式中:λ为反映材料拉压强度不等性质参数(λ= σc/σt,根据试验实测值来确定)；b为中间主应力对能量释放的影响系数。

上述2种准则都是基于能量耗散与释放的原理进行推导分析的,认为能量释放量Gc正比于所积蓄的弹性能Ue,假设能量释放率为K,则有

其中:

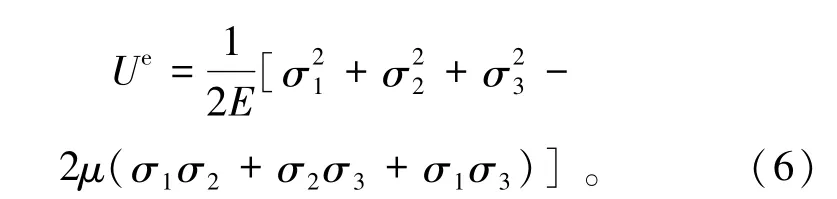
式中E为岩石卸载弹性模量。能量释放量与3个主应力大小以及它们之间的主应力差有密切关系,但是前者以能量释放量正比于单元中储存的可释放能量,并按与最小压应力的差进行分配；后者虽考虑中间主应力效应,但是考虑的形式应该还可以进一步的一般化。

工程岩体多属于三向受压应力状态,因此本文主要研究三向受压的应力状态。为了能更一般地考虑中间主应力对岩石强度的影响,本文假设能量释放分配系数为F(σ1,σ2,σ3),则

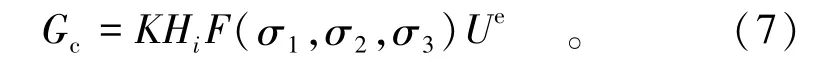
式中Hi(i=1,2,3)为材料常数。为了确定能量准则通式中的材料常数Gci,可参考文献[1]和文献[3]采取代特殊值办法来确定,即

将式(8)代入式(7),此时分配系数的一般数学形式为

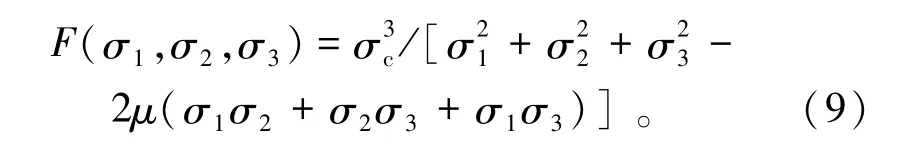
3 中间主应力效应分析

中间主应力对岩石强度的影响研究已有几十年历史了,得到了许多有意义的结论和规律,本文从能量释放的角度来分析中间主应力效应。

由第2节可知,岩石能量释放与各主应力均有关系,并推导得到了相应的分配系数公式(9)。为了分析中间主应力在岩石能量释放的分配中所起到作用及其规律,笔者利用文献[14-15]中的拉西瓦花岗岩、文献[16]中的红砂岩、文献[17]中的中细砂岩以及文献[14]中的Dunham白云岩的真三轴试验资料(见表1和表2)分别进行数据分析。

在分析中间主应力σ2的作用时,σ3为固定值,且σ1随着σ2变化而变化,此时有

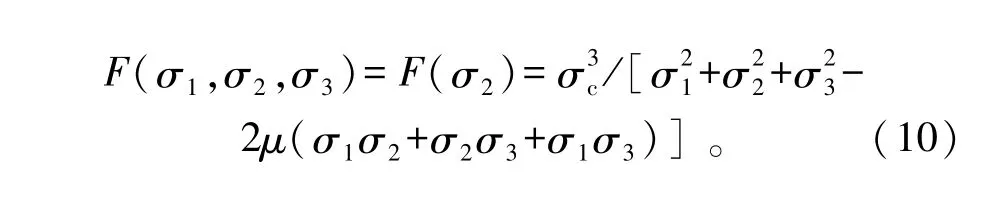
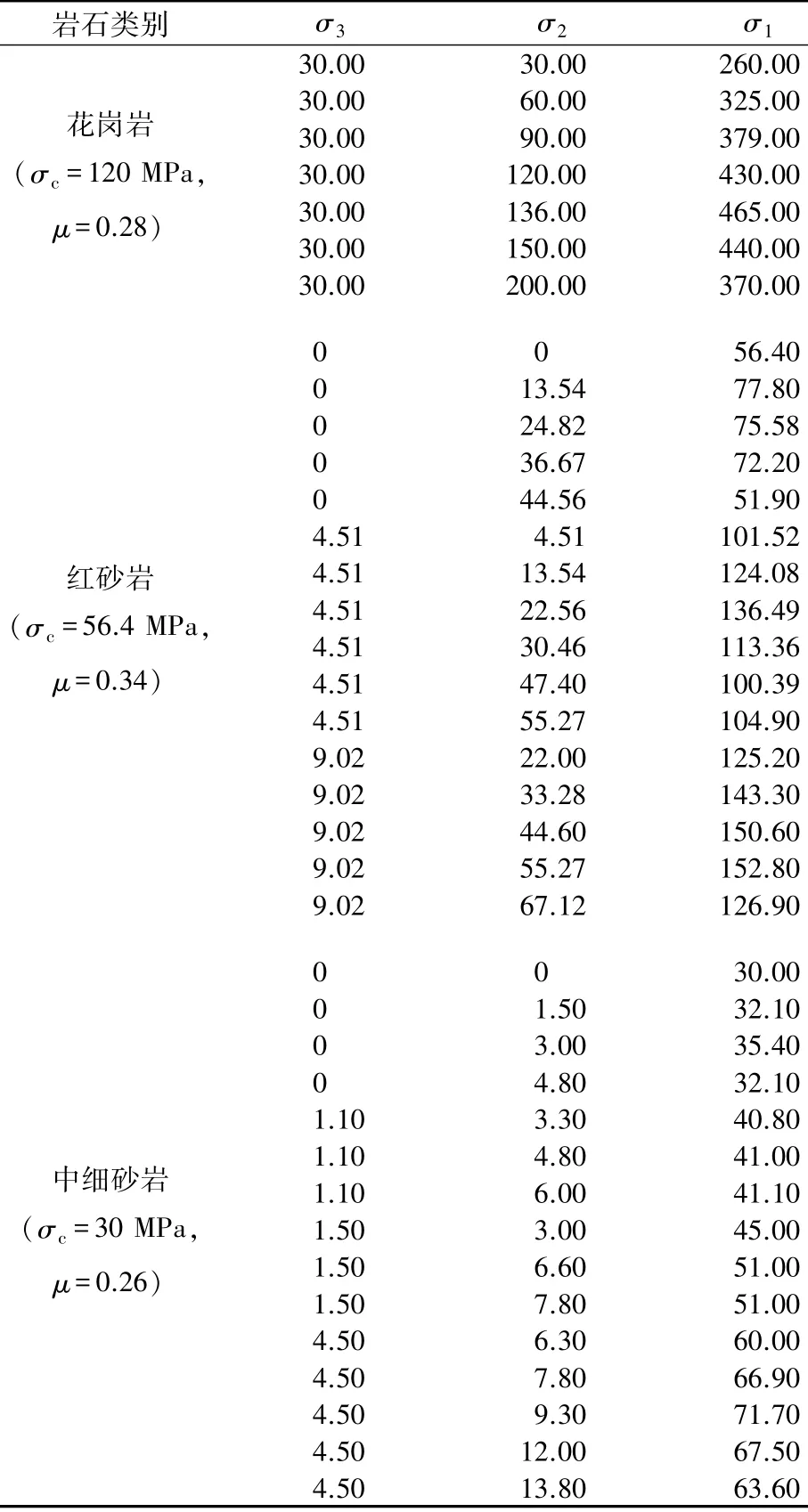
表1 拉西瓦真三轴试验数据［14-17］Table 1 True triaxial experiment data of Laxiwa hydropower station［14-17］MPa

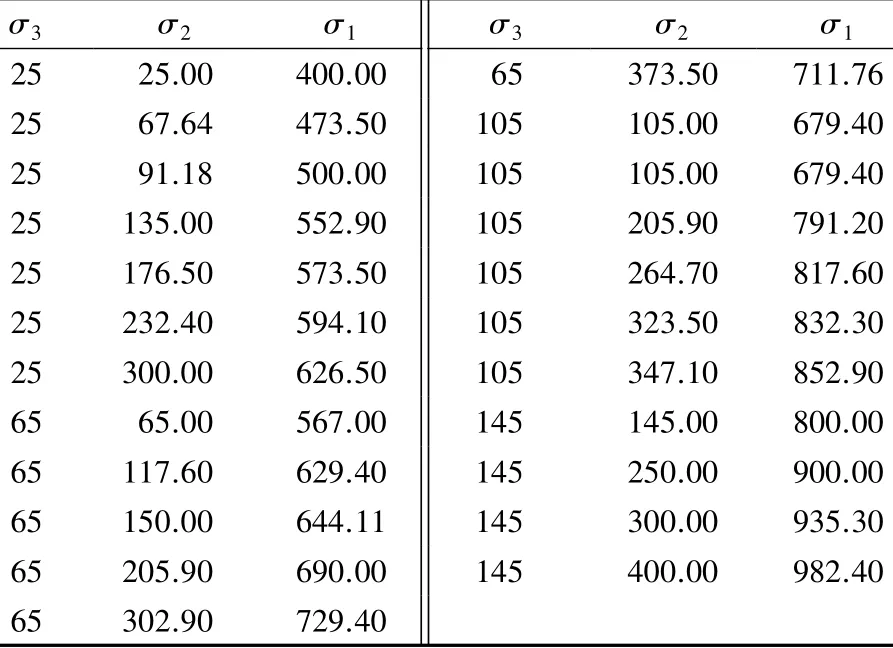
表2 Dunham白云岩真三轴试验数据［14］Table 2 True triaxial experiment data of Dunham dolomite［14］MPa

由式(6)和式(10)可知,Ue与分配系数成负相关,当分配系数较小时Ue较大,也就意味着可释放应变能较大。根据能量释放及能量耗散的思想可知,Ue极限为破坏表面能U0,因此此处所说的Ue主要是指特定主应力状态下的极限状态即破坏表面能U0。而破坏表面能从另一个角度来看相当于岩石强度。换言之,在分配系数降低时岩石强度是增大的。

在最小主应力固定的情况下,中间主应力主导能量释放分配系数(F(σ2))的变化。根据式(10)分析文献[14-17]中的数据(见图1),结合图1可知:

(1)中间主应力的提高可以促使能量释放分配系数降低,而这也意味着可使岩石的极限抗压强度提高。

(2)中间主应力效应具有区间性,即在σ3一定的情况下,能量释放分配系数随着σ2值的增加刚开始是逐步降低的,当其达到某一最低值后,随着σ2值的增加而上升。

(3)随着σ3值的增加,F(σ2)-σ2曲线不断下降,曲线谷值不断降低。

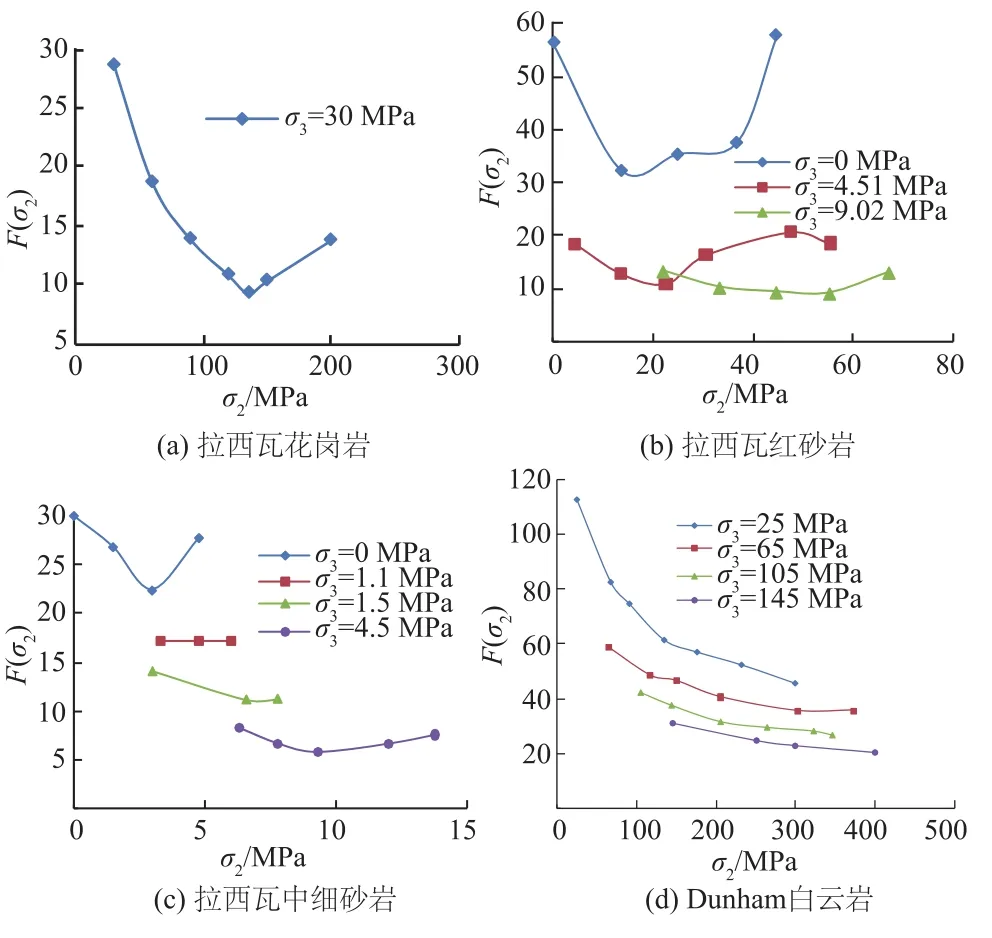
图1 拉西瓦3种岩石及Dunham白云岩的F(σ2)-σ2关系曲线Fig.1 Relation curves of F(σ2)-σ2of Dunham dolomite and three kinds of rock in Laxiwa

4 新强度准则的建立

4.1 新强度准则

结合第3节分析,岩石强度在受到中间主应力效应影响的同时,最小主应力σ3对强度的影响也很明显。随着σ3值的增加,F(σ2)-σ2曲线不断下降,曲线谷值不断降低,即随着σ3值的增加,相应的极限强度(σ1)随之增加。

能量释放分配系数F(σ2)与σ1的关系如图2所示。

图2 拉西瓦3种岩石及Dunham白云岩的F(σ2)-σ1关系曲线Fig.2 Relation curves of F(σ2)-σ1of Dunham dolomite and three kinds of rock in Laxiwa

从图2可知,在σ3为定值时,能量释放分配系数F(σ2)与σ1基本呈线性关系,具体参数见表3。

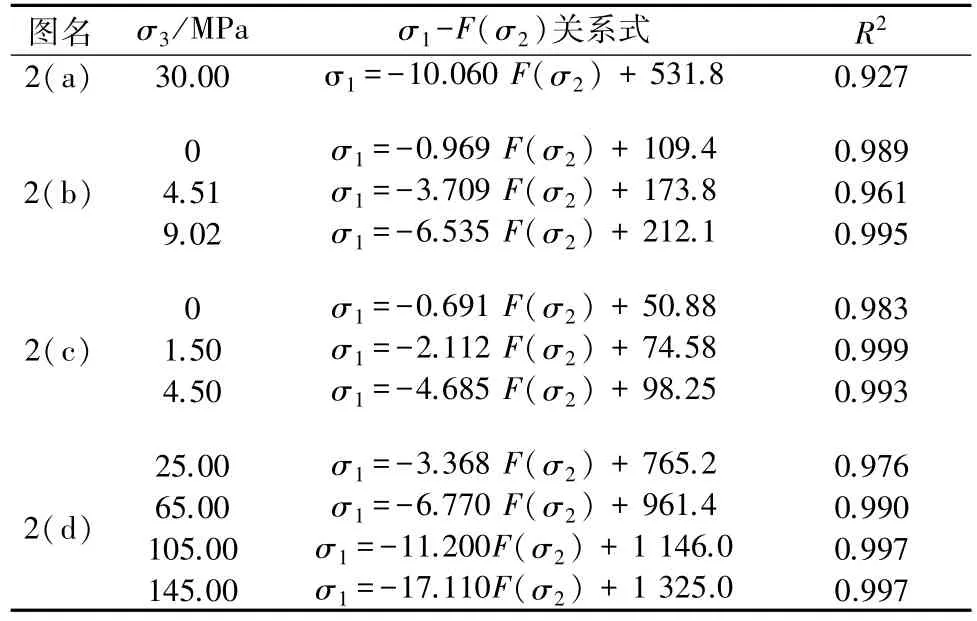
表3 试验数据拟合参数Table 3 Fitting parameters of test data

根据能量释放分配系数与极限强度之间的关系可以推导出新的强度准则形式,即

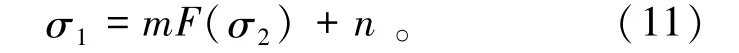
式中m,n均为拟合系数。

分析式(11)可知,当F(σ2)=0时,σ1=n,即n的物理含义为在σ3为定值且理想情况下,岩石的最大极限强度,这也是中间主应力的影响下的最大值。但此时式(11)仅考虑了σ2影响下的能量释放率,而从图2(b)至图2(d)也可以看出随着σ3变化,m,n也随之改变,拟合公式及R2见表4。

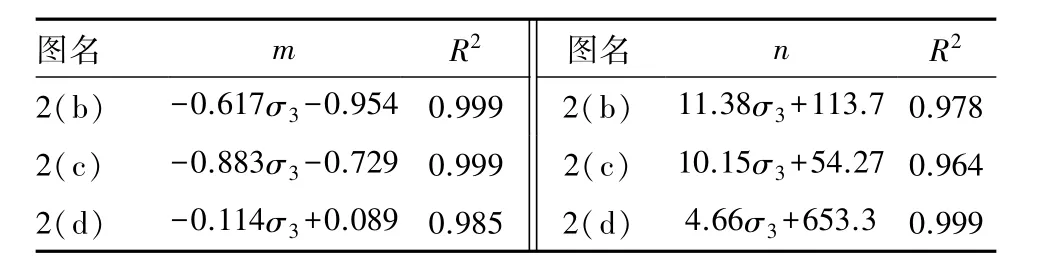
表4 图2中F(σ2)-σ1的拟合公式及R2值Table 4 F(σ2)-σ2fitting formula in Fig.2 and the value of R2

式中a1,a2,b1,b2为岩石材料参数,可由试验获取。

4.2 新强度准则的验证

岩石强度准则提出的最终目的是为了应用,即在生产或研究的过程中可以正确地预测岩石的极限强度。因此,下面对强度准则的实用性做出验证。验证数据采用文献[18]的真三轴试验数据(岩石材料参数σc=170 MPa,μ=0.21),见表5。

则根据上述分析可知

表5 真三轴试验数据［18］Table 5 True triaxial test data［18］MPa

验证方法为:将一部分试验数据作为原始数据,并以此求得上述强度准则中所需参数。然后根据所得参数及式(11),式(12)计算出相应的σ3,σ2下的最大主应力σ1。

根据表5中数据可得到:a1=-0.106,b1= -0.977；a2=10.85,b2=330.0。则

将文献[18]中的数据代入式(13)计算并与试验数据对比(见表6)。从表中可以看出计算所得结果与试验结果的相对误差不超过±10%。从σ3=0 MPa的计算结果可以看出,最大主应力σ1的增加速率为先增加然后趋于平稳,符合岩石强度受中间主应力效应影响的一般规律；对比σ3=0 MPa及σ3= 2 MPa的计算结果,随着最小主应力增加,最大主应力σ1逐渐增大。因此本文所提出的强度准则模式在考虑了中间主应力影响,又结合了最小主应力的作用,因此更为接近实际情形。

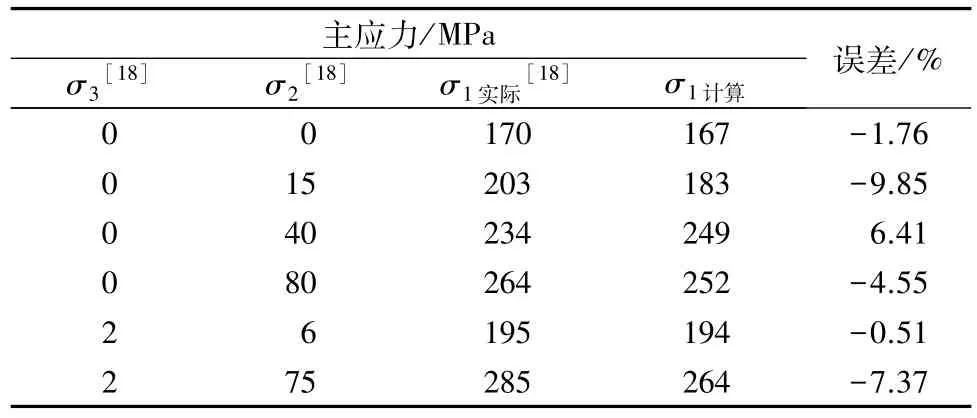
表6 理论计算结果与试验数据对比Table 6 Contrast of theoretical calculation result and experimental data

5 结 论

本文基于能量原理研究了中间主应力对岩石强度的影响,并结合最小主应力,提出了新的能量强度准则,以此为基础结合前人的研究得出以下结论:

(1)从能量耗散与能量释放的角度,研究中间主应力对岩石强度的影响,与前人所得规律基本一致,说明运用能量原理研究中间主应力效应是可行的。

(2)在最小主应力σ3一定时,能量释放分配系数与岩石极限强度成线性关系,且随着能量释放分配系数的提高岩石极限强度逐渐降低。

(3)基于前人研究成果及中间主应力效应的分析,可以获得岩石能量释放基于应力分配的一般形式。

(4)基于能量原理和中间主应力效应可以建立岩石新的能量强度准则,能弥补原有强度准则多没有考虑中间主应力影响的不足。

[1]谢和平,鞠 杨,黎立云.基于能量耗散与释放原理的岩石强度与整体破坏准则[J].岩石力学与工程学报, 2005,24(17):3003-3010.(XIE He-ping,JU Yang,LI Li-yun.Criteria for Strength and Structural Failure of Rocks Based on Energy Dissipation and Energy Release Principles[J].Chinese Journal of Rock Mechanics and Engineering, 2005,24(17):3003-3010.(in Chinese))

[2]谢和平,彭瑞东,鞠 杨.岩石变形破坏过程中的能量耗散分析[J].岩石力学与工程学报,2004,23(21):3565-3570.(XIE He-ping,PENG Rui-dong,JU Yang.Energy Dissipation of Rock Deformation and Fracture[J].Chinese JournalofRockMechanicsandEngineering,2004, 23(21):3565-3570.(in Chinese))

[3]张后全,徐建峰,贺永年,等.脆性岩石真三轴能量强度准则研究[J].中国矿业大学学报,2012,41(4):564-570.(ZHANG Hou-quan,XU Jian-feng,HE Yong-nian,et al.Study of Triaxial Energy Strength Criterion for Brittle Rock Materials[J].Journal of China University of Mining& Technology,2012,41(4):564-570.(in Chinese))

[4]高 红,郑颖人,冯夏庭.岩土材料能量屈服准则研究[J].岩石力学与工程学报,2007,26(12):2437-2443. (GAO Hong,ZHENG Ying-ren,FENG Xia-ting.Study on Energy Yield Criterion of Geomaterials[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(12): 2437-2443.(in Chinese))

[5]孙 倩,李树忱,冯现大,等.基于应变能密度理论的岩石破裂数值模拟方法研究[J].岩土力学,2011,32(5): 1575-1582.(SUN Qiang,LI Shu-chen,FENG Xian-da,et al.Study of Numerical Simulation Method of Rock Fracture Based on Strain Energy Density Theory[J].Rock and Soil Mechanics,2011,32(5):1575-1582.(in Chinese))

[6]刘新荣,郭建强,王军保,等.基于能量原理盐岩的强度与破坏准则[J].岩土力学,2013,34(2):305-317(LIU Xin-rong,GUO Jian-qiang,WANG Jun-bao,et al.Investigation on Mechanical Properties and Failure Criterion of Salt Rock Based on Energy Principles[J].Rock and Soil Mechanics,2013,34(2):305-317.(in Chinese))

[7]潘 岳,王志强,李爱武.岩石失稳破裂的综合刚度和综合能量准则[J].岩土力学,2009,30(12):3671-3676. (PAN Yue,WANG Zhi-qiang,LI Ai-wu.Comprehensive Rigidity and Comprehensive Energy Criterion of the Rock Burst[J].Rock and Soil Mechanics,2009,30(12):3671-3676.(in Chinese))

[8]三三○设计院研究室.中细砂岩不等压三轴强度的初步试验研究[J].岩土力学,1979,(1):47-61.(Laboratory of 330 Design Institute.Primary Experimental Study of non-equal Triaxial Strength of Middle Thin Gritstone[J]. Rock and Soil Mechanics,1979,(1):47-61.(in Chinese))

[9]许东俊,幸志坚,李小春,等.RT3型岩石高压真三轴仪的研制[J].岩土力学,1990,(2):1-14.(XU Dong-jun, LI Xiao-chun,et al.XING Zhi-jian.Manufacture of RT3 Rock High Press Ture Triaxial Instrument[J].Rock and Soil Mechanics,1990,(2):1-14.(in Chinese))

[10]MOGI K.Fracture and Flow of Rocks[J].Tectonophysics, 1972,13(1):541-568.

[11]MOGI K,IGARASHI K,MOCHIZUKI H.Deformation and Fracture of Rocks under General Triaxial Stress States: Anisotropic Dilatancy[J].Journal of the Society of Materials Science,1978,27(293):148-154.

[12]李小春,许东俊.中间主应力对岩石强度的影响程度和规律[J].岩土力学,1991,12(1):9-16.(LI Xiao-chun, XU Dong-jun.Law and Degree of Effect the Intermediate Principle Stress on Strength of Rock[J].Rock and Soil Mechanics,1991,12(1):9-16.(in Chinese))

[13]许东俊,耿乃光.岩石强度随中间主应力变化规律[J].固体力学学报,1985,(1):72-80.(XU Dong-jun,GENGNai-guang.The Variation Law of Rock Strength with Increase of Intermediate Principal Stress[J].Acta Mechanica Solida Sinica,1985,(1):72-80.(in Chinese))

[14]MAO Hong-yu,YUE Wen-zan,JIAO Zhao,et al.A Unified Strength Criterion for Rock Material[J].International Journal of Rock Mechanics and Mining Sciences,2002,39 (8):975-989.

[15]尤明庆.统一强度理论的试验数据拟合及评价[J].岩石力学与工程学报,2008,27(11):2193-2204.(YOU Mingqing.Fitting and Evaluation of Test Data Using Unified Strength Theory[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(11):2193-2204.(in Chinese))

[16]高延法,陶振宇.岩石的强度准则的真三轴压力试验检验与分析[J].岩土工程学报,1993,15(4):26-32. (GAO Yan-fa,TAO Zhen-yu.Examination and Analysis of True Triaxial Compression Testing of Strength Criteria of Rock[J].Chinese Journal of Geotechnical Engineering, 1993,15(4):26-32.(in Chinese))

[17]张金铸,林天键.三轴试验中岩石的应力状态和破坏性质[J].力学学报,1979,15(2):99-105(ZHAN Jinzhu,LIN Tian-jian.Stress Conditions and the Variation of Rupture Characteristics of A rock as Shown by Triaxial Tests[J].Chinese Journal of Theoretical and Applied Mechanics,1979,15(2):99-105.(in Chinese))

[18]陈景涛.高地应力下硬岩本构模型的研究与应用[D].武汉:中国科学院研究生院(武汉岩土力学研究所), 2006.(CHEN Jin-tao.Research and Application of Constitutive Model of Hard Rock under High Ground Stress[D]. Wuhan:Institute of Rock and Soil Mechanics,Chinese A-cademy of Sciences,2006.(in Chinese))

(编辑:黄 玲)

第六届长江委重大成就奖专题———林绍忠副院长喜登榜首

2015年9月,长江水利网专题推出“匠人情怀,智者风范———第六届长江委重大成就奖专题”,深度报道为推进治江事业发展作出重要贡献的7位获得者,长江科学院副院长兼总工林绍忠以“专注”为关键词喜登榜首。

大家可登陆长江水利网第六届长江委重大成就奖专栏(http://www.cjw.gov.cn/xwzx/ztjjx/zdcj6/)查看专题文字报道《水工结构领域的“计算专家”———记长江科学院副院长兼总工林绍忠》及相关视频,也可关注长江委公众微信号“美丽长江”进行查看。

(摘自：长江水利科技网)

Discussion on New Rock Strength Criterion Based on Energy Principle and Intermediate Principal Stress Effect

NIU Chao-ying,JIA Hong-biao,MA Shu-zhi,WANG Kang
(Faculty of Engineering,China University of Geosciences,Wuhan 430074,China)

Energy conversion is the physical feature in physical process.Through analyzing the rule of energy variation in the process of rock damage and relations of the rule,strength,and integral destruction,the essential feature of variation of rock strength and the overall destruction under external load was reflected.From the perspectives of energy dissipation and energy release,based on previous research achievements and effect of intermediate principal stress,general form of energy release of rock based on stress distribution was presented.Combined with minimum principal stress,a new strength criterion was suggested.Results show that,it is feasible to study the effect of intermediate principal stress by using energy criterion.When the value of minimum principal stress is given,relationship between rock ultimate strength and distribution coefficient of energy release is linear.Moreover,with the increase of distribution coefficient of energy release,the ultimate strength of rock gradually decreases.New energy strength criterion can fully consider the influence of intermediate principal stress,which can make up the shortage of conventional rock damage criterions.

rock mechanics；energy strength criterion；intermediate principal stress；distribution coefficient of energy release；minimum principal stress

TU45

A

1001-5485(2015)11-0093-06

10.11988/ckyyb.20140479

2014-06-10；

2014-07-14

牛超颖(1988-),女,河南焦作人,硕士研究生,主要从事岩土工程及岩石力学方面的研究,(电话)18275538439(电子信箱) 275466451@qq.com。