一个分数阶超混沌系统及其在图像加密中的应用

薛 薇，肖 慧，徐进康，贾红艳

(天津科技大学电子信息与自动化学院，天津 300457)

一个分数阶超混沌系统及其在图像加密中的应用

薛 薇，肖 慧，徐进康，贾红艳

(天津科技大学电子信息与自动化学院，天津 300457)

对一个同量分数阶超混沌Qi系统进行仿真分析，绘制了该分数阶系统的相轨迹图、Poincaré截面映射图、Lyapunov指数谱图和分岔图，仿真结果验证了该分数阶系统的混沌特性．在此基础上，将该分数阶超混沌Qi系统应用于数字图像加密，并对密文的直方图、相邻像素相关性、密钥敏感性等进行分析．结果表明：基于分数阶超混沌Qi系统的图像加密算法具有密钥空间大、安全性高等特点．

分数阶；超混沌Qi系统；仿真分析；图像加密

1963年，Lorenz[1]提出了著名的Lorenz混沌系统数学模型及混沌理论的基本特征．之后，许多学者相继提出一些新的混沌系统，如Chen系统[2]、Lü系统[3]、Liu系统[4]、Qi系统[5]等，使得混沌动力学在非线性研究领域取得了重大的发展．由于混沌系统具有内随机性、不可预测性、宽带特性、遍历性以及对初始条件和系统参数的极端敏感性等，因此，混沌系统及其应用研究引起学者们极大的研究热情．尤其是近年来，随着分数阶微积分理论的发展和应用，一些学者将分数阶微积分算子引入混沌系统中，生成分数阶混沌系统并对其进行研究[6–9]．研究表明，当混沌系统为分数阶时，系统仍然能呈现出混沌状态，且更能反映系统所呈现的实际物理现象[10–11]．因此，研究分数阶混沌系统及其在各个领域的应用更具有普适性和实用价值．

混沌变换所具有的对参数和初值的敏感性等基本特性及其与密码学的天然关系早在Shannon[12]的经典文献中就已提到，并据此提出了密码学中用于指导密码设计的2个基本原则：扩散和混乱．现在混沌动力学正由数学和物理的基础理论研究逐步过渡到实际的工程应用领域，并得到了很大发展，例如混沌理论可用在保密通信、图像加密等信息领域[13–15]．

自Matthews[16]提出混沌加密思想以来，有关混沌密码和混沌保密通信方案的研究逐步成为研究热点．以往研究混沌加密技术大多数基于低维整数阶混沌系统，虽然低维混沌系统由于形式简单而具有计算时间短的优点，但其密钥空间小、序列的复杂度不高，导致密码系统的安全性不高．而高维混沌系统尤其是超混沌系统，由于具有4个及以上的状态变量，因此密钥空间更大，这些特点使得超混沌系统用于图像加密会提高系统的安全性．随着人们对分数阶混沌系统研究的深入，发现分数阶混沌系统除具有整数阶混沌系统对初值敏感性、伪随机性等优良特性外，还具有分数阶混沌系统所特有的一些性质，如能够反映系统的历史信息、很强的历史记忆性等[17]．分数阶混沌系统增强了系统的非线性和复杂性，可增大密码系统的密钥空间[18]．并且，利用现有的整数阶混沌分析和预测方法并不能估计出分数阶混沌系统的分数阶次，即现有的整数阶混沌系统分析和预测方法对分数阶混沌系统失效．因此，有必要探索研究基于分数阶混沌系统的数字图像加密方法．考虑到Qi系统与Chen系统、Liu系统等系统相比较，数学模型在不增加复杂度的情况下，既可以产生两翼的混沌吸引子，又可以产生四翼的混沌吸引子，其动力学特性更为复杂．所以，本文针对一个同量分数阶超混沌Qi系统及其在图像加密中的应用进行研究．

1 分数阶超混沌Qi系统的数值分析

文献[19]中提出了超混沌Qi系统，这个四维超混沌系统是通过对文献[5]中的混沌系统引入一个线性反馈控制器得到的．本文在文献[19]的基础上，分析同量分数阶超混沌Qi系统，数学模型如下：

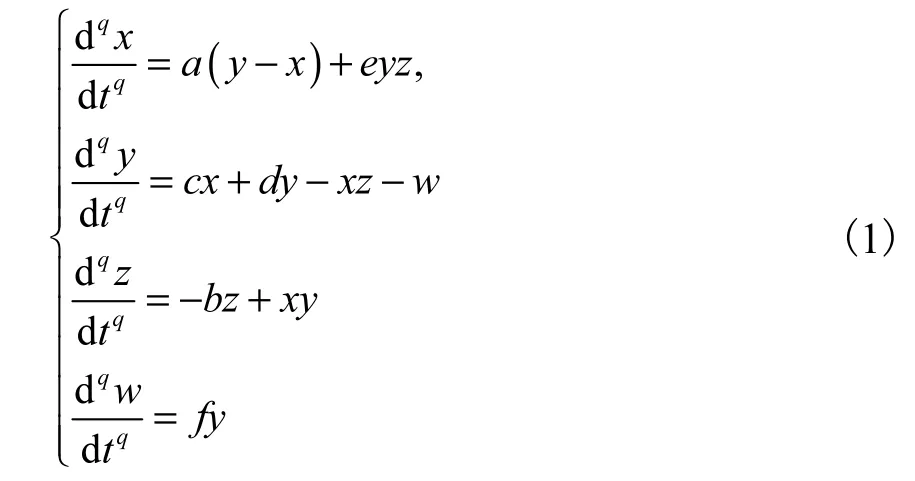
其中0＜q＜1．当a=15，b=40，c=−5，d=20，e=5，f=50时，可绘制式(1)系统随阶次q变化的分岔图如图1所示．

从图1中可以看出q∈[0.761,1]时，式(1)系统呈现混沌态，这里选取q=0.9，对3.6阶超混沌Qi系统进行仿真分析和研究．

图1 式(1)系统随q变化的分岔图Fig.1 Bifurcation diagram of system shown by equation (1) on x axis with parameter q

1.1 相轨迹图

当取参数a=15，b=40，c=−5，d=20，e=5，f=50，q=0.9时，分数阶超混沌Qi系统的相轨迹如图2所示．

图2 式(1)系统的相轨迹图Fig.2 Phase portraits of the system shown by equation (1)

1.2 Lyapunov指数及分岔图

Lyapunov指数(L)可以表征系统运动特征，它沿某一方向取值的正负和大小，表示系统长时间在吸引子中相邻轨道沿该方向平均发散(L＞0)或收敛(L＜0)的快慢程度．对于超混沌系统必然存在2个或2个以上正的Lyapunov指数．该分数阶超混沌系统随参数a变化的Lyapunov指数谱图和分岔图分别如图3和图4所示．

图3 式(1)系统随参数a变化的Lyapunov指数谱图Fig.3 Lyapunov exponent diagrams of system shown by equation (1) with parameter a

由图3和图4可以看出，式(1)系统随参数a变化时的分岔图与其对应的Lyapunov指数谱图一致．此外，系统的Lyapunov指数L4始终小于－10，为了方便观察，y轴截取为[−10,10]，如图3(b)所示．当a=15时，L1=2.199，L2=0.4077，L3=0，L4=−44.64，该系统是超混沌的．随着参数a的改变，式(1)系统平衡点的稳定性将会发生改变，从而系统也将处于不同的状态．a分别取15、16、35时，式(1)系统呈现混沌、周期、拟周期等不同的动力学特性，相轨迹如图5所示．

图4 式(1)系统随参数a变化在x方向上的分岔图(a∈[0,60])Fig.4 Bifurcation diagram of the system shown by equation (1) on x axis with parameter a(a∈[0,60])

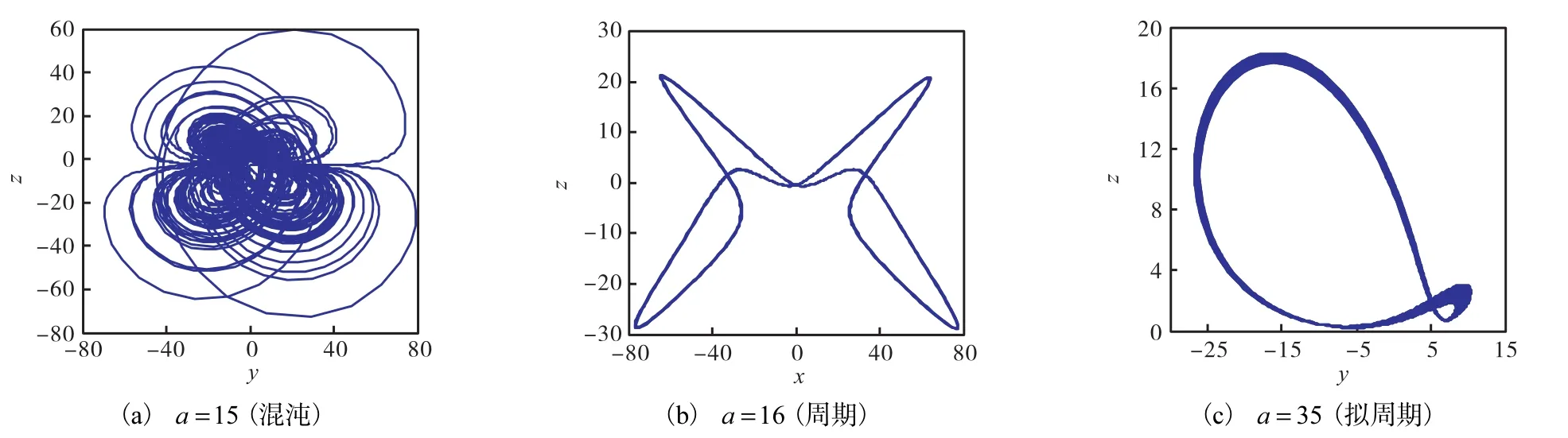
图5 系统(1)在参数a取不同值时的相轨迹图Fig.5 Phase portraits of system (1) with different a

1.3 Poincaré截面

当a=15时，式(1)系统在x=25和y=10处两个截面上的Poincaré映射见图6，Poincaré截面是一些具有分形特征的密集点，说明系统是混沌或超混沌的.

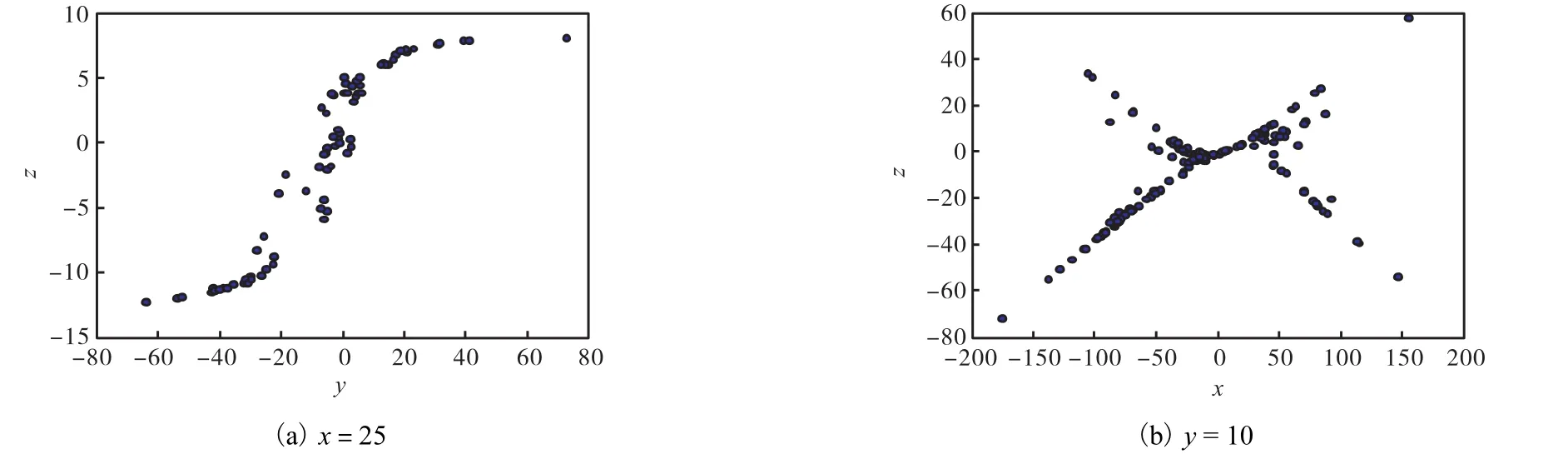
图6 式(1)系统的Poincaré映射图Fig.6 Poincaré map of the system shown by equation (1)

2 分数阶超混沌Qi系统在图像加密中的应用

2.1 彩色图像的加密与解密

彩色图像是由RGB三基色来描述的，即图像在计算机中的存储是m×n×3的矩阵形式，而分数阶超混沌Qi系统是一个四维连续自治系统．因此，采用一维时域乱序加密再三维空域加密的算法．加密与解密流程见图7．

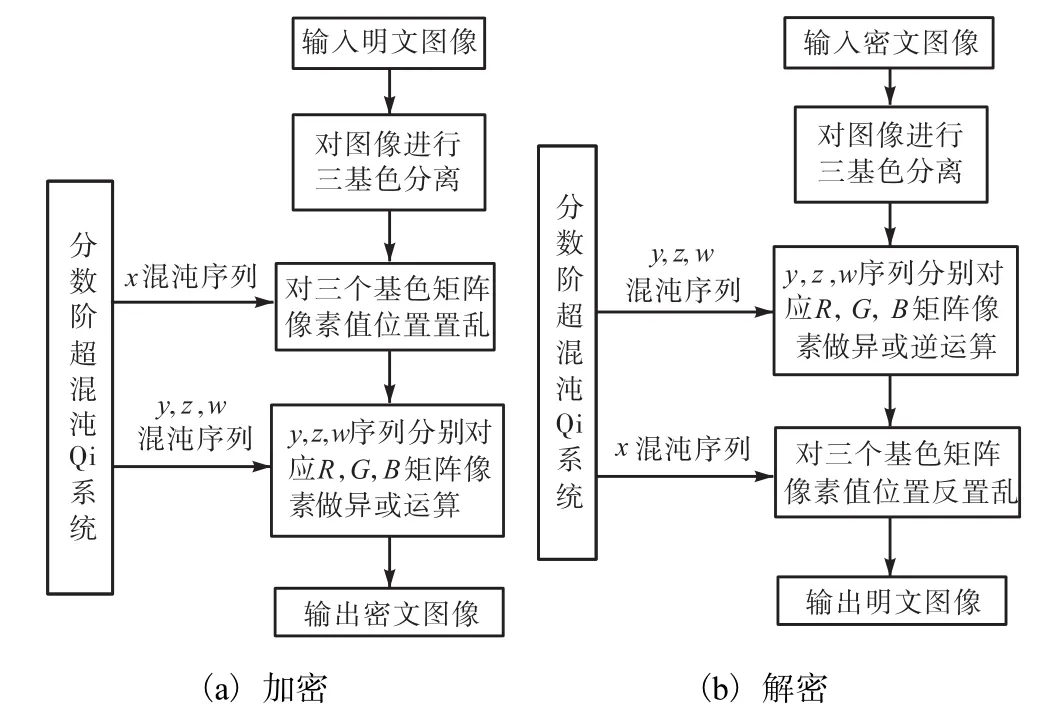
图7 加密与解密流程图Fig.7 Flow chart of encryption and decryption

最后得到彩色图像的加密结果如图8(a)所示，解密结果如图8(b)所示．

图8 原始图像的加密与解密结果Fig.8 Results of encryption and decryption

2.2 算法安全性分析

2.2.1 密钥敏感性分析

取系统参数q=0.9，a=15，b=40，c=−5，d=20，f=50，系统初始值x0=y0=z0=w0=0.1为密钥，对图像进行加密．当输入正确的密钥时，可解密成功得到正确的解密图像如图8(b)所示，图9为将初始值改为x0=y0=z0=w0=0.100 000 000 001，其他参数值不变时，解密失败的图像．可以看出：很微小的密钥变化也不能成功解密图像，测试结果表明该加密系统对密钥具有较高的敏感性．

图9 错误密钥解密结果Fig.9 Decryption result of the wrong key

2.2.2 直方图分析

图10为加密前后R基色分量的灰度直方图，描述图像中各灰度级的像素个数．可以看出：加密前各灰度级的像素分布波动较大，波峰波谷间差值较大；加密后各灰度级的像素分布比较均匀，各灰度级的像素出现的频率基本相同，很好地掩盖了原图像的分布规律，能够很好地抵抗统计分析的攻击．

图10 图像加密前后R基色的直方图Fig.10 Histograms before and after image encryption

2.2.3 相邻像素的相关性分析

分别从原始图像和加密后图像中任取一行、一列像素点进行相邻像素相关系数计算，求得图像在水平、垂直相邻像素的相关系数见表1．由表1结果可知：此算法的加密信号具有较好的扩散和混淆．原始图像的相邻像素的相关系数接近1，具有高度相关性．而加密后的相关性系数接近0，相邻像素已基本不相关．因此，该算法对统计分析的攻击具有更好的安全性．

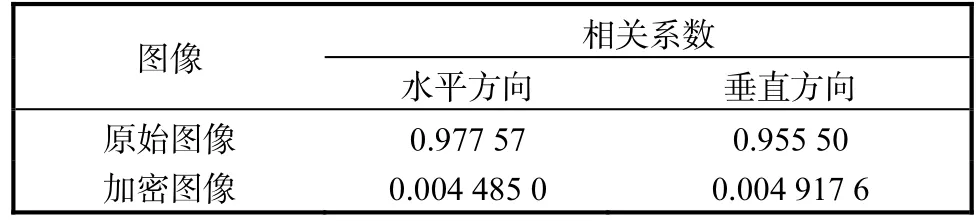
表1 相邻像素的相关系数Tab.1 The correlation of adjacent pixels

3 结 语

本文分析了同量分数阶超混沌Qi系统的混沌特性，计算并绘制了该分数阶超混沌系统的Lyapunov指数图、分岔图、Poincaré截面映射图等，验证了该分数阶超混沌吸引子的存在性．最后，将该分数阶超混沌系统应用于彩色图像加密，采用一维时域乱序加密三维空域再加密的算法，利用所提出的分数阶超混沌Qi系统对数字图像进行加密，并对该算法的安全性进行分析．分析表明，该算法具有密钥敏感性强、密文分布均匀、密文相邻像素的相关性低等特点，说明了分数阶超混沌Qi系统在图像加密中的应用具有较好的前景．

［1］ Lorenz E N.Deterministic non-periodic follow[J].Journal of Atmospheric Sciences，1963，20：130–141.

［2］ Chen G R，Ueta T.Yet another chaotic attractor[J].International Journal of Bifurcation and Chaos，1999，9(7)：1465–1466.

［3］ Lü J H，Chen G R.A new chaotic attractor coined[J].International Journal of Bifurcation and Chaos，2002，12(3)：659–661.

［4］ Liu C X，Liu L，Liu T，et al.A new butterfly-shaped attractor of Lorenz-like system[J].Chaos，Solitons and Fractals，2006，28(5)：1196–1203.

［5］ Qi G Y，Chen G R，van Wyk M A，et al.A four-wing chaotic attractor generated from a new 3-D quadratic autonomous system[J].Chaos，Solitons and Fractals，2008，38(3)：705–721.

［6］ Jia H Y，Chen Z Q，Xue W.Analysis and circuit implementation for the fractional-order Lorenz system[J].Acta Physica Sinica，2013，62(14)：140503-1–140503-7.

［7］ Huang L L，Xin F，Wang L Y.Circuit implementation and control of a new fractional-order hyperchaotic system[J].Acta Physica Sinica，2011，60(1)：010505-1–010505-9.

［8］ Grigorenko I，Grigorenko E.Chaotic dynamics of the fractional Lorenz system[J].Physical Review Letters，2003，91(3)：034101-1–034101-4.

［9］ Li C P，Peng G J.Chaos in Chen’s system with a fractional order[J].Chaos，Solitons and Fractals，2004，22(2)：443–450.

［10］ Hifer R，Butzer P L，Westphal U，et al.Applications of Fractional Calculus in Physics[M].New Jersey：World Scientific，2001.

［11］ Zhou P，Wei L J，Cheng X F.A novel fractional-order hyperchaotic system and its synchronization[J].Chinese Physics B，2009，18(7)：2674–2679.

［12］ Shannon C E.Communication theory of secrecy systems[J].Bell System Technology Journal，1949，28(4)：656–715.

［13］ Li W，Hao J H，Qi B.An encryption approach to chaos synchronization communications by using CPRNG [J].Acta Physica Sinica，2008，57(3)：1398–1403.

［14］ Peng Z P，Wang Ch H，Lin Y，et al.A novel fourdimensional multi-wing hyper-chaotic attractor and its application in image encryption[J].Acta Physica Sinica，2014，63(24)：240506-1–240506-10.

［15］ Yu Ch Y，Zhu J L，Guo J Y.Four-dimensional hyperchaotic system and application research in signal encryption[J].Electric Machines and Control，2012，16(3)：96–100.

［16］ Matthews R.On the derivation of a “chaotic” encryption algorithm[J].Cryptologia，1989，13(1)：29–42.

［17］ Wang Q Y，Zhou S B.Image encryption algorithm based on fractional-order Chen chaotic system[J].Journal of Computer Applications，2013，33(4)：1043-1406.

［18］ Wu X，Wang H，Lu H.Modified generalized projective synchronization of a new fractional-order hyperchaotic system and its application in secure communication[J].Nonlinear Analysis：Real World Applications，2012，13(3)：1441–1450.

［19］ Xue W，Qi G Y，Mu J J，et al.Hopf bifurcation analysis and circuit implementation for a novel four-wing hyperchaotic system[J].Chinese Physics B，2013，22(8)：329–336.

责任编辑：常涛

A Fractional-order Hyper-chaotic System and its Application in Image Encryption

XUE Wei，XIAO Hui，XU Jinkang，JIA Hongyan
(College of Electronic Information and Automation，TIanjin University of Science & Technology，Tianjin 300457，China)

A commensurate fractional-order hyper-chaotic Qi system was analyzed by means of numerical simulation including drawing its phase portraits，Poincaré maps，Lyapunov exponent spectra and bifurcation diagrams.Simulation results verified the chaotic characteristics of the fractional order system.After that the application of the fractional-order hyperchaotic Qi system to image encryption was investigated，and the histogram，adjacent pixels correlation，key sensitivity of the ciphertext were analyzed.Results show that the algorithm of image encryption based on fractional hyper-chaotic Qi system has a large key space and high security.

fractional-order；hyper-chaotic Qi system；simulation analysis；image encryption

TN919.82

A

1672-6510(2015)05-0067-05

10.13364/j.issn.1672-6510.20140157

2014–12–05；

2015–02–04

国家自然科学基金青年基金资助项目(11202148)

薛 薇（1963—），女，河北河间人，教授，xuewei@tust.edu.cn.

数字出版日期：2015-05-08；数字出版网址：http://www.cnki.net/kcms/detail/12.1355.N.20150508.1454.001.html.