半潜式钻井平台承载力极限状态设计
2015-01-03张延昌王自力
张延昌 刘 昆 王 璞 王自力
(1.中国船舶及海洋工程设计研究院 上海200011; 2.江苏科技大学 船舶与海洋工程学院 镇江212003)
引 言
深水钻井装备是勘探开发深海油气资源的关键,也是制约我国石油公司进军深海的主要瓶颈之一。目前世界主流的深水钻井装置有半潜式钻井平台和钻井船两种,相对于钻井船,半潜式钻井平台下浮体潜入水中,甲板处于水上安全高度,水线面面积小,受波浪影响小,稳性和运动性能好,适应海域广,是应用最广泛的深水钻井装置[1](如图1和图2)。2012年5月9日,我国首座自主设计建造、代表世界先进水平的第六代半潜式深水钻井平台“海洋石油981”号在南海荔湾6-1区域开钻,标志着我国海洋石油工业向深远海迈出了实质性一步。

图1 半潜式钻井平台效果图(GVA7500)

图2 “海洋石油981”号半潜式钻井平台
近20年以来,船舶结构设计方法从传统的许用应力准则设计向极限状态设计转变,极限状态设计能够考虑结构各种形式的失效模式,更为精确、经济、安全。海洋工程结构、陆地结构日益趋向于采用极限强度的设计方法。国际标准化组织ISO曾颁布的 ISO 18072系列[2-3](草稿)、IACS共同规范[4-5]以及各船级社规范[6-7]均对船舶船体梁的极限强度(极限弯矩)作出具体规定。国际船舶与海洋结构大会ISSC[8-10]连续几届对极限强度撰写专题报告,DNV标准[7]也给出极限状态设计的指导性意见,但对分析方法、准则、分析手段等并没有详细叙述。对于海洋工程-半潜式钻井平台来说,基于承载力极限状态设计还是一个难度较大的新颖课题。
1 承载力极限状态
船舶与海洋工程结构设计是在传统船舶结构设计的基础上,按照法规、规范要求,运用先进科学的分析方法和手段进行结构设计,在具备足够安全可靠的基础上实现既定的功能,设计方法随着人们对结构物以及环境认识的深入逐步提升。船舶结构设计方法从传统的许用应力分析法向极限状态设计转变,极限状态设计能够考虑不同的结构失效模式,真实、全面、系统地反映全寿命期内结构安全性,更为理性、经济、科学。
极限状态是指结构系统中部分构件或整体结构失效,导致其丧失应有的设计功能所对应的状态,而能够承受特定模式的失效情况下(如疲劳、断裂、屈服等),结构所具有的强度即称为极限状态。国际船舶与海洋结构大会ISSC技术报告[10]及Paik[11]对四种极限状态(使用极限状态SLS、承载力极限状态ULS、疲劳极限状态FLS、事故极限状态ALS)进行了阐述。承载力极限状态又称极限强度,指由于结构刚度或强度的丧失而导致结构崩溃失效,下页图3反映了承载力极限状态设计。考虑塑性影响进行简化修正得到的屈曲强度作为简化极限状态设计如图中A点为结构弹性屈曲强度,这种简化方法使结构设计者不需要清楚了解实际结构材料进入塑性后的后屈曲特性以及结构之间的相互作用,故无法准确描述结构实际极限承载力,也就是图中B点。研究确定结构在B点位置出的极限承载力就能清楚反映结构实际安全裕度。目前,海洋工程结构日益趋于采用极限强度的设计方法。

图3 基于ULS的结构设计示意图
作为深海钻井的主力,深海半潜式钻井平台相关的研究设计是国内外学者的研究热点。Cyranka和Videiro[12]用有限元软件ANSYS模拟工作在巴西Campos流域1 360 m水深的P-36半潜式平台所发生的紧急排污舱破裂崩溃。该半潜平台随后又因一系列人为误操作而发生易燃气体爆炸、平台进水,最终在6天后沉没。Chakrabarti等[13]对一艘半潜式钻井船在失去撑杆而主体结构完整情况下的剩余承载能力进行有限元计算,并论述海洋平台结构物与传统船舶计算极限承载能力时在计算工况及计算方法上的不同。
Estefen等[14]对一艘新型的半潜式平台,研究了立柱横框架间加筋板的破坏机理,将加筋板的极限承载能力数值解与小尺度实验解进行对比,并对立柱进行逐步破坏的分析。曾常科、肖熙[15]采用简化逐步破坏法计算某半潜平台的平台浮体和平台整体的极限强度;杨鹏[16]采用简化逐步破坏法对半潜式平台极限强度进行分析计算;姜峰等[17]采用非线性有限元法计算半潜式平台局部结构的极限强度。本文作者也曾对船体板架数值仿真分析技术、半潜式钻井平台水平横撑、上部船体结构的极限承载力进行数值仿真分析[18-20]。由于承载力极限状态设计还是一个难度较大的新颖课题,其研究还处于起步阶段,关于半潜平台的极限状态设计的分析方法、准则、分析手段等还不够成熟,也没有规范可以参考。中国船舶及海洋工程设计研究院曾联合江苏科技大学对半潜平台结构极限强度分析技术进行全面系统研究,并指导结构设计。本文在此研究成果的基础上,对承载力极限状态设计在半潜式钻井平台中应用技术进行总结。
2 极限强度分析技术
2.1 半潜式平台极限强度计算方法
对于半潜式平台在海洋环境条件下受力特点、载荷传递方式、结构变形模式等与单船体结构有显著的不同,因此,半潜式平台极限强度分析比船体梁弯曲极限强度更为复杂,在计算工况、计算方法等方面都有些差异。
2.1.1 计算工况
极限强度作为衡量结构在外力作用下抵抗变形和破坏最大能力的指标,理论上需要考虑到各种有可能的危险工况进行计算。传统的船舶结构通常被简化船体梁模型来计算极限强度,载荷效应主要考虑危险工况下船体梁总纵弯矩即可。对半潜式平台来说,ABS船级社MODU规范[21]给出半潜式平台强度分析需要考虑主要的载荷模式,针对其构造型式、结构刚度、载荷效应等特点,从中选取几种主要工况作为半潜式平台的极限强度的计算分析工况,以变形模式定义如下:
(1)横向分离模式。指横向波浪作用而产生横向分离载荷效应,如下页图4所示,半潜式平台遭受波长等于2倍的平台型宽的横向来浪,横向分离载荷达到最大值。

图4 半潜式平台横向分离模式
(2)纵剪模式。指斜浪作用下发生的纵向剪切效应,如图5所示,半潜式平台遭受波长等于1.5倍的平台对角长度的斜向来浪,纵向剪切载荷达到最大值。
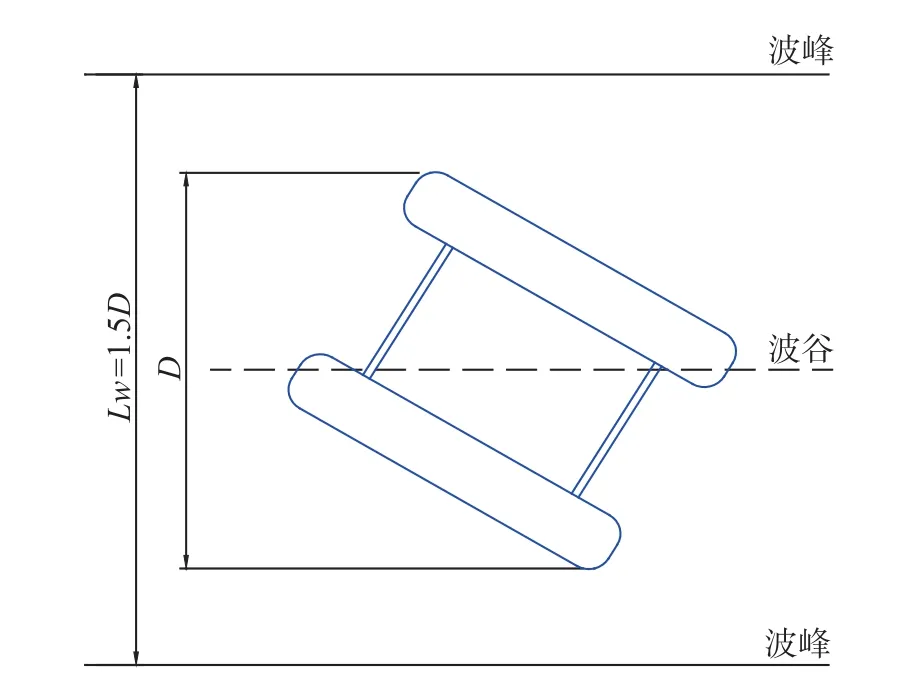
图5 半潜式平台纵剪模式
(3)纵扭模式。指斜浪作用下发生的绕水平x轴的扭转效应,简称纵扭。如图6所示,半潜式平台遭受波长等于平台对角长度的斜向来浪,纵向扭转载荷达到最大值。

图6 半潜式平台纵扭模式
2.1.2 计算方法
对于船体梁极限强度主要有四种计算方法:直接计算法、简化逐步破坏法、非线性有限元法和理想结构单元法。对于结构型式、载荷模式等均较复杂的半潜式平台来说,直接计算法、简化逐步破坏法、理想结构单元法并不适用于分析整体平台横向分离、纵剪、纵扭载荷模式下的极限承载力。计算机技术的发展,使得非线性有限元法成为计算半潜平台极限强度的主流方法,有限元法在模拟结构渐进失效过程具有独特的优势。
非线性有限元法是一种能较为准确真实地模拟结构渐进屈曲过程的方法,可以考虑材料、几何等非线性问题,也可考虑结构之间的相互影响,采取合理的模型化技术适用于各种型式的结构。随着计算机硬件、软件的发展,对于大型海洋结构极限强度分析来说,有限元方法是最主要分析方法之一,并具有独特优势。结构分析时有限元软件的选择、分析技术等均很重要,需要开展系列研究,形成可靠的分析技术。目前用于结构极限强度分析的商业 有 限 元 软 件 有 ABAQUS、MARC、ANSYS、LSDYNA等。
2.2 极限强度数值仿真分析技术
在计算复杂结构整体极限强度时,由于需考虑几何非线性与材料非线性,往往耗时较大,对计算机性能要求较高;同时,计算过程中会遇到迭代不收敛、计算精度较差等问题,要得到正确可靠的计算结果,需对极限强度数值仿真分析技术开展研究。
本文作者[18]以文献[22] 中船体板架为研究对象,根据文献提供的结构参数、模型边界等资料,采用ABAQUS软件[23]分析研究了数值仿真分析技术,其中包括网格大小、单元属性、分析步参数以及材料本构关系等对计算结果的影响,主要结论如下:
(1)网格越密,其计算结果越准确(与文献结果相比),但当网格密度达到一定程度之后,极限承载力基本不变。对于大型结构物来说,应通过试算确定合理的网格密度,即能保证结果的精度,又可提高计算效率。
(2)对于 ABAQUS软件中 S4R、S4、S4R5三种单元,S4R5单元更适用于计算面内载荷为主要载荷模式下的结构极限强度,用于后续平台极限承载力仿真计算。
(3)对于采用弧长法进行分析时,初始时间增量主要对达到极限后的失效模式及承载力影响较大。初始时间增量减小时,计算容易收敛但耗时也就增多,应根据计算规模计算确定合理的初始时间增量。
(4)材料模型可选取简化的理想弹塑性模型,也可使用真实应力塑性应变曲线,理想弹塑性模型得到的计算结果偏于保守。
在此基础上,本文从分析方法、初始缺陷、极限承载力确定、计算结果分析等方面进行分析,对极限强度数值仿真技术进行补充完善。
2.2.1 分析方法研究
在极限强度有限元法中,有三种分析方法:准静态法、弧长法、阻尼因子法[24],本文对准静态法、弧长法两种方法对研究对象进行分析。在采用准静态进行结构极限承载力计算时,选择0.1 mm/s、0.5 mm/s、1 mm/s三种加载速度进行分析计算,载荷-位移曲线如图7所示,准静态法得到的计算结果明显高于弧长法的结果。不同加载速度对结构极限载荷极值及载荷-位移曲线均产生显著的影响,计算结果随着加载速度的降低而减小。弧长法在求解非线性较高的结构体系具有较好的适用性,能够有效处理空穴和突弹跳变问题;但结构规模较大时,采用这种方法容易出现收敛性问题。采用该方法关键是选择合适的加载速率,加载速率过大将会导致求解结果的局部性(剧烈的局部变形),使结果偏离“准静态”的要求;而过慢的加载速率则意味较长的加载时间,使计算时间大幅增加。通过分析对比结构在计算过程中的动能与其应变能之比是否小于5%来判断加载速率是否合适。

图7 准静态法、弧长法计算载荷-位移曲线
2.2.2 初始变形影响
焊接裂纹、残余应力、焊接变形、腐蚀等缺陷以及船舶制造装配、营运过程中产生的永久性相对变形都会对结构极限强度产生影响,本部分参考DNV规范使用极限状态衡准对板架变形的要求,选取0.2 t、0.5 t、1.0 t作为板格初始变形进行分析。从图8所示载荷-位移曲线可以看出:随着初始挠度的增加结构极限承载力迅速下降,载荷-位移曲线的弹性加载段的范围缩小。通过对渐进损伤变形模式分析,对于0.5 t、1.0 t两种初始变形结构首先在初始变形施加区域,而初始挠度为0.2 t结构的屈曲并不是发生在初始缺陷区域。因此,初始缺陷对结构的极限承载能力存在较大的影响,若焊接变形控制在规范规定的范围内(<0.2 t),则对结构极限承载力影响不大。数值仿真分析考虑初始变形可参考规范对变形的要求,也可采用实际测量的变形量。

图8 不同初始变形下板架载荷-位移曲线
2.2.3 结果分析技术
极限载荷和变形模式是有限元数值仿真结果分析的主要对象。有限元软件能够反映每一步长(时刻)的结构变形,为结果分析提供方便,通过变形云图可以分析结构构件变形、失效方式;同时每个构件的失效将会影响到载荷-位移曲线的走势,结构的变形、失效模式载荷-位移曲线是协调统一的。因此,结果分析时要将两者结合来分析评估结构极限强度特性。
结构极限承载力(又称极限载荷)是结构极限承载能力的主要指标,极限载荷主要是通过对结构的逐步加载,测出试件对应特征变量(关键部位的应变或位移),绘制载荷-变形曲线,根据极限载荷定义方法,从载荷-变形曲线上确定实验极限载荷。陈钢[25]介绍了根据“显著塑性流动”的判据的定义准则,如:切线交点准则、塑性模量准则、0.2%残余应变准则、两倍弹性变形准则、两倍弹性斜率准则、Demir-Drucker准则等。本文作者[26]曾对半潜式钻井平台管道钢构支架极限进行了实验、数值仿真研究,分析了不同准则的影响。对半潜式平台3种载荷模式下载荷-位移曲线进行分类,可分成如图9所示两种形式,分别定义为分叉模式和非分叉模式。对于分叉模式的载荷-位移曲线,峰值载荷即为极限载荷极;对于非分叉模式的曲线,可以采用两倍弹性斜率准则(即tanφ= 2tanθ)确定极限载荷。
3 半潜平台极限强度数值仿真分析
3.1 有限元模型
3.1.1 结构有限元模型
本部分以完整平台结构为研究对象,主要包括上部船体、立柱、水平横撑和下浮体,考虑到计算效率,不包括主甲板上的局部舱室或结构,如生活楼、设备间、井架等。有限元模型中仅包括甲板板、舱壁板等板材以及较大桁材的腹板,较小桁材、骨材、面板等构件均未考虑。本文第3.3节中将讨论结构简化处理方式对计算结果的影响。
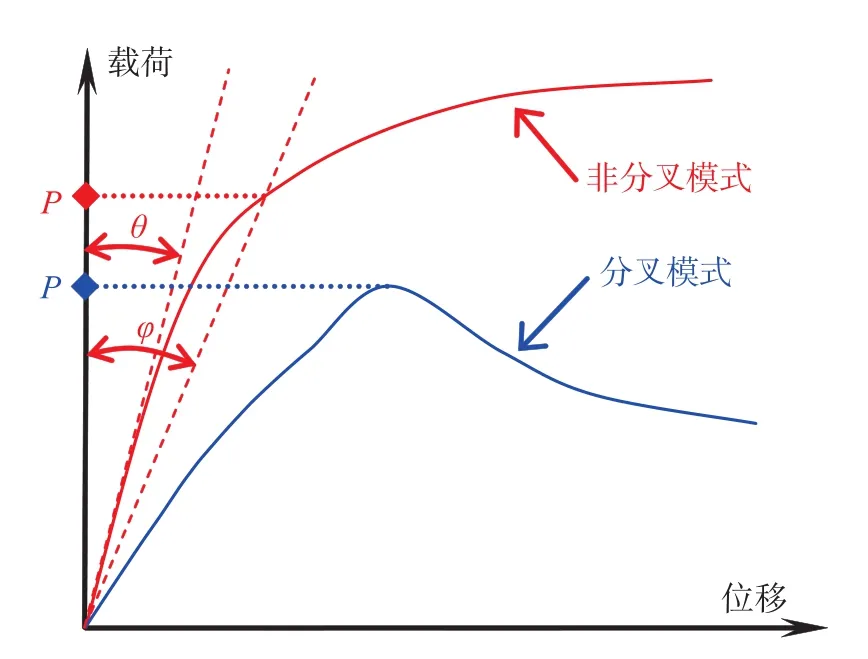
图9 载荷-位移曲线——分叉、非分叉模式
由非线性有限元软件ABAQUS建立整个平台结构有限元模型,结构网格大小为肋骨间距,立柱与上部船体局部连接区域采用较细网格尺寸。板单元采用四边形单元S4R5,部分采用三角形单元STRI3,材料模型为理想弹塑性模型,屈服强度为315 MPa。
3.1.2 载荷模型及边界条件
采用准静态法进行分析过程中,载荷施加位置、方式等对计算结果的合理性至关重要,载荷简化处理要考虑到半潜式平台结构型式特点、载荷传递过程、载荷模式等方面。半潜式平台下浮体受到波浪载荷作用,这些载荷首先作用于下浮体,再经立柱传递于上部船体、横撑结构,载荷由上部船体、横撑承受。因此,有限元仿真分析时位移载荷施加于下浮体。载荷施加方式是通过定义参考点并与其中一个下浮体外侧板(或底板)整个平面所有节点耦合,约束参考点的运动自由度,定义参考点速度来实现的。
实际平台处于自由漂浮状态,六个方向的运动均处于自由状态,而数值仿真分析时需要约束整体运动,根据载荷模式采取不同的约束处理方式,合理的简化尤为重要。本文作者曾对边界约束对计算结果的影响进行分析,限于篇幅,此处不再赘述。三种载荷模式下较合理的处理方式如下页表1所示。

表1 三种载荷模式下载荷边界模型
3.2 计算结果分析
3.2.1 横向分离模式
计算得到载荷-位移曲线及d=1.0 m位置对应的变形、应力云图分别如图10和下页图11所示。载荷位移曲线可分:弹性加载段、塑性变形段、塑性流动段(卸载段)三阶段。在弹性加载段随着结构位移增加载荷呈线性增加,随着部分构件发生屈曲、屈服失效后,结构继续承载能力下降,随着位移增加承载能力下降速度急剧增加,位移曲线进入卸载段或明显塑性流动阶段。横向分离、挤压两种变形下极限承载力分别为209 MN、194 MN。前者曲线为非分叉模式,结构达到极限承载力后还具备继续承载的能力,在该极限载荷下不会引起失效的进一步扩展;后者属于分叉模式,当达到极限载荷结构失效后,结构承载能力迅速减低,很快发生整体崩溃。这也说明横向挤压载荷模式更值得关注。

图10 载荷-位移曲线——横向分离模式
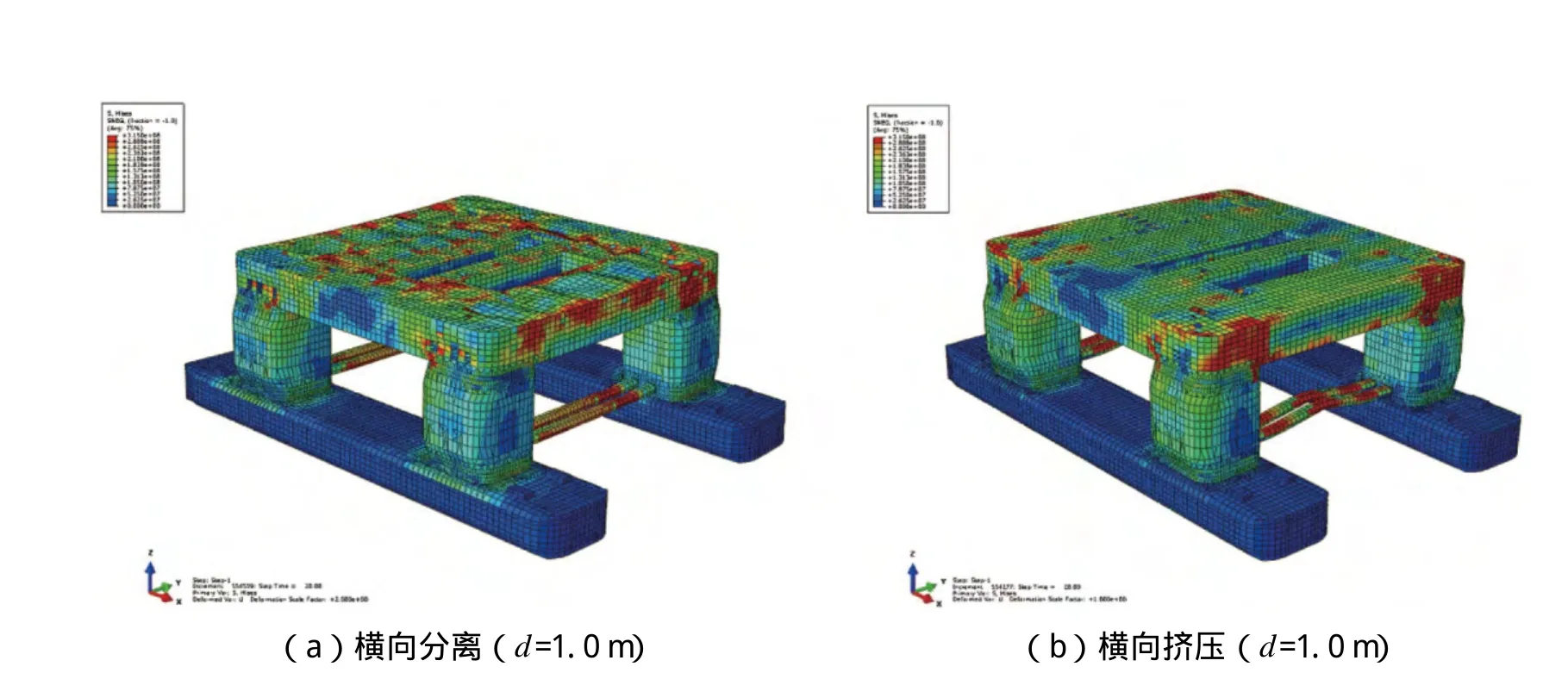
图11 损伤变形、应力云图——横向分离模式
通过ABAQUS软件计算时,首次计算很难判断计算时间间隔是否合适,本项目采用多次计算的方法使计算数据点增加。第一次计算时选取较大的时间间隔(20 s)使结构完全进入塑性流动或完全失效,计算得到载荷位移曲线;然后根据载荷位移曲线确定第二次计算的时间(10 s),这样使得载荷位移曲线在塑性阶段的数据点加密,对极限承载力确定更精确。
通过分析系列变形云图可反映出整个平台结构在横向载荷下结构失效的过程、失效区域及相应的失效模式。在弹性阶段,水平撑杆是主要的承载构件,当拉应力先达到315 MPa时,进入屈服失效状态;随后载荷发生转移,载荷位移曲线进入塑性阶段。载荷主要由上部船体承受,上部船体主甲板、横向纵壁板上缘等结构处于受压缩状态,更易于产生屈曲失效,主甲板屈曲标志着进入明显塑性流动阶段。下甲板处于受拉伸状态,主要产生屈服失效模式,但在纵向立柱与甲板开孔之间的下甲板连接局部区域载荷模式较复杂,产生明显的高应力,易发生屈曲、屈服变形。随着甲板塑性变形的增加,甲板围壁也发生较大的塑性变形,结构达到极限状态。限于篇幅,横向挤压损伤变形过程分析省略。
3.2.2 纵剪模式
计算得到纵剪模式下载荷-位移曲线及d= 2.0 m位置对应的变形、应力云图分别如图12和图13所示。纵剪模式下载荷-位移曲线为非分叉模式,采用两倍弹性斜率方法得到极限载荷为101.5 MN。载荷位移曲线可分为三段:弹性段、塑性变形段、明显塑性流动阶段。从变形云图中看出,在下浮体受到纵向剪力作用时,载荷由立柱传递于平台甲板,在纵向剪力下主要承载构件为上部船体结构;在剪切作用下甲板开口角隅处结构产生明显的应力集中;甲板结构开口间区域结构的塑性变形并不明显,开口结构四周有围壁结构,使得开口区域的扭转刚度较大,不易发生扭转变形;在立柱间的甲板区域发生较为明显的塑性变形。立柱结构内侧围壁结构是剪切载荷传递的主要构件,该区域结构的应力较高;立柱结构内部结构较强,结构刚度较大,立柱结构并没有发生屈曲和较大的塑性变形。

图12 载荷-位移曲线——纵剪模式

图13 损伤变形、应力云图——纵剪模式
3.2.3 纵扭模式
计算得到纵扭模式下载荷-位移曲线及d= 2.0 m位置对应的变形、应力云图分别如图14和图15所示。纵剪模式下载荷-位移曲线为非分叉模式,采用两倍弹性斜率方法得到极限剪力为61.7 MN、扭矩为3 740 MN·m。位移载荷通过下浮体、立柱传递到平台甲板及水平横撑,主要由上部船体甲板承受。平台甲板受到扭转变形,发生较大变形的区域为甲板开口两侧、立柱之间的甲板结构,结构失效主要由该区域的结构决定。靠近立柱结构的水平横撑结构、开口周围及立柱附近区域的结构扭转刚度相对较大,该区域的变形相对较小。

图14 载荷-位移曲线——纵扭模式
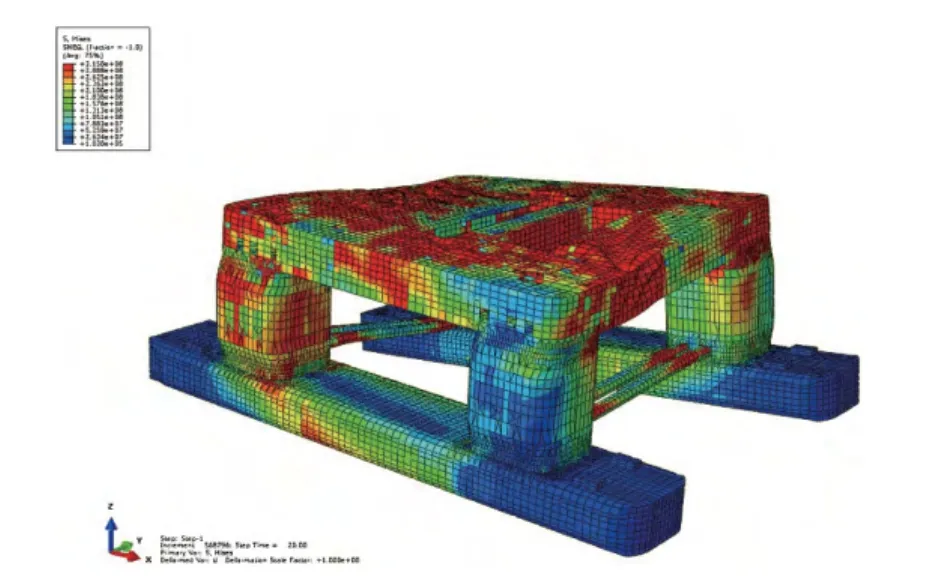
图15 损伤变形、应力云图——纵扭模式
3.3 结构模型简化方式影响分析
对于由加筋板架构成的海洋工程结构,局部骨材、板等小构件的屈曲、屈服失效是结构整体失效的基本组成因素,结构模型中能够准确反映这些构件的失效过程,对取得真实合理的计算结果尤为重要。
本部分对骨材、面板等小构件的处理方式分以下三种处理方式,分析构件简化处理对计算结果的影响,加筋有限元模型如图16所示。极限承载力计算结果如下页表2所示。从计算结果来看,骨材不同的处理方式对各载荷模式计算结果产生不同程度的影响。加筋模型计算结果最大,板材模型结果最小。等效板厚模型的计算结果比板材模型计算结果略大,不同载荷模式提高程度不同,其中扭转模式极限载荷提高最大;加筋模型相比等效模型,横向分离极限载荷提高30%左右,横向挤压极限载荷仅提高1%左右。

图16 加筋有限元模型

表2 极限承载力计算结果汇总
采用加筋模型进行分析更能确切模拟实际结构,但加筋模型的计算时间相当长。本文计算采用DELL图形工作站Studio XPS9100(主要配置CPU:Intel Core8核,主频2.67 GHz,内存6 G,硬盘1 TG),对于板材模型(单元总数约为7.6万)——横向分离载荷工况,分析损伤过程为20 s(位移1.0 m),计算机耗时约为2 h;而对于加筋模型(单元总数约为8.9万)——横向分离载荷工况,分析损伤过程为7 s(位移为0.35 m),计算机耗时约为150 h。考虑到计算效率问题,采用计算效率较高的等效板厚处理方式进行极限强度分析在工程上更切实可行。
4 基于承载力极限状态的结构设计
基于承载力极限状态的结构设计流程图如图17所示,其中包括目标平台极限承载力数值仿真分析、设计载荷预报、极限强度衡准、极限强度评估及优化设计等环节。本文第3章详细介绍了半潜式钻井平台承载力数值仿真分析,本章将对其余环节进行介绍。
4.1 设计载荷预报
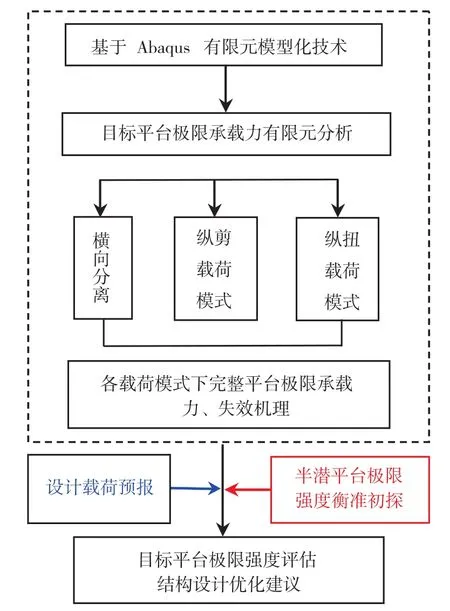
图17 基于承载力极限状态的结构设计流程图
承载力极限设计状态是考虑钻井平台在整个生命周期内的可能遇到的极值载荷作为设计载荷,通常以超越概率的形式表示,平台技术规格书或设计基础文件将对设计环境条件进行描述。本文目标平台考虑百年一遇的极端海洋环境,利用DNV船级社SESAM/GeniE软件建立半潜平台湿表面模型、质量模型,由HydroD模块计算半潜平台在单位波幅规则波上的力和运动响应,即船体响应的传递函数;由Postresp模块按百年一遇的设计条件进行船体波浪诱导运动和载荷的短期统计预报,并预报极值进行分析,确定目标平台的设计载荷。波浪载荷短期预报详细的分析过程、具体参数等不再赘述,本文给出主要的计算结果如下页表3所示,选取生存工况和作业工况两工况下的最大载荷作为设计载荷。

表3 半潜平台设计载荷短期统计预报值
4.2 校核衡准初探
结构极限强度评估受到载荷、载荷效应、结构性能评估的不确定性等诸多不确定性因素的影响,结构设计需要结构具有足够的安全裕度,各船级社规范通常采用部分安全系数准则考虑诸多的不确定性,如式(1)所示:
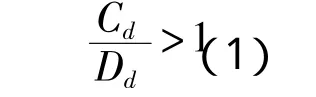
CSR、DNV、ABS等船级社给出了船体梁极限弯矩的校核衡准,这些衡准的共同特点是:
(1)适用对象是船体梁,且仅局限于船体梁弯矩。
(2)采用部分安全系数准则,都是基于式(1)的基础上得到的。本部分以部分安全系数准则为指导思想,结合半潜式平台极限强度计算分析工况,考虑半潜式平台极限强度的三种主要的变形模式(横向分离、纵剪、纵扭),初步提出适用于完整结构极限强度校核的衡准,具体如表4所示。其中设计载荷为半潜平台在作业、拖航、生存等工况下环境载荷极值(包括静水和波浪部分);极限承载力为各单一变形模式下结构的极限承载能力,由非线性有限元法计算得到。
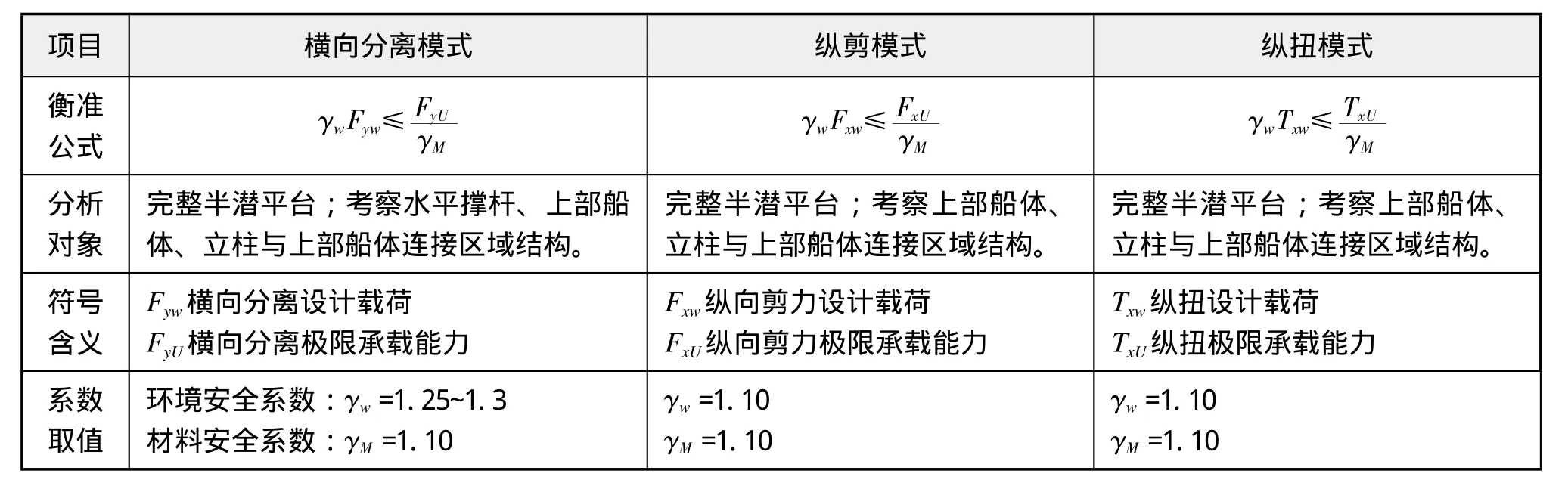
表4 半潜式平台极限强度衡准
4.3 极限强度评估
采用本文提出的极限强度衡准对目标平台在三种载荷模式极限强度下进行评估,结果如下页表5所示。等效模型考虑了局部加筋构件对整体极限承载力的影响,计算效率较高,相对安全。因此,以该模式有限元计算结果作为完整平台的极限承载力。从该表可看出该目标平台整体极限强度满足要求,并有一定的裕度;相对于其它两种模式,平台在横向分离载荷(尤其是在横向挤压模式下)的利用系数(U.C.=Dd/Cd)较大;另外,该模式下的载荷曲线为分叉模式,峰值后结构承载能力迅速下降。因此,横向挤压变形模式下的极限强度需要重点关注。

表5 半潜式平台极限强度校核结果
4.4 结构设计优化建议
通过对三种变形模式下结构的损伤变形、应力云图可以清楚地反映结构在各载荷模式下的损伤机制,也反映了载荷的传递过程及主要承载构件,研究成果为结构优化设计指明了方向。
(1)水平横撑结构在横向挤压下首先发生失效,横撑结构的失效将会导致平台整体结构极限承载力的迅速下降。水平横撑结构比较重要,设计时应重点关注,其中包括总体外形尺寸、局部板架结构匹配、与立柱之间连接等方面。
(2)载荷通过立柱传递至上部船体,上部船体结构是主要承载构件,上部船体结构需重点关注:
① 上部船体结构整体刚度;
② 左右立柱间纵向舱壁、月池开口区域甲板等结构在剪切、扭转等载荷下的屈曲强度;
③ 上部船体与立柱连接区域结构在复杂受力下的屈曲、屈服强度以及两者之间的刚度匹配。
(3)提高易于发生屈曲、屈服的局部结构的承载能力会提高平台整体的承载力,分析首先发生屈曲、屈服失效的区域,对其增加结构尺寸是一种有效方式。通过改变结构型式、调整相邻结构的刚度等方式可使结构刚度匹配更合理,也可提高结构承载能力。
5 结 论
本文基于非线性软件ABAQUS,以加筋板架为例研究了分析方法、初始变形影响、结果分析技术等仿真分析技术;针对目标半潜式钻井平台分析研究了横向分离、纵剪、纵扭三种变形模式下的极限承载力及结构损伤变形模式,分析等效模型、加筋模型对计算结果以及计算效率的影响;初步提出适用于半潜式平台极限强度的衡准,并对目标平台进行评估。主要结论如下:
(1)本文较为系统全面地对半潜平台极限强度进行研究,提出基于承载力极限状态的结构设计流程、思路及数值仿真分析技术,为后续研究及工程设计提供指导和帮助。
(2)半潜式钻井平台构造型式、结构、载荷模式等均较复杂,非线性有限元法是极限承载力分析有效手段;合理、高效的数值仿真分析技术是计算结果真实可信的切实保障。
(3)研究表明目标平台极限强度满足要求,并具有一定的裕度。平台在横向挤压模式下的利用系数较大,考虑到半潜式平台横向挤压变形呈现出分叉模式,该载荷模式下横撑结构其关键作用,采用加筋模型获得的极限承载力提高程度较小;同时横撑结构细长,易于受到损伤。因此,横向挤压下完整平台极限强度、横撑结构及横撑与立柱相连接结构应着重考虑。
(4)整体平台结构的承载能力取决于局部关键结构,从数值仿真计算结果云图可发现率先发生局部失效的结构(如左右立柱间纵向舱壁、月池开口区域、上部船体与立柱连接区域结构),增加易于失效结构的尺寸或调整结构间的刚度匹配是提高结构承载力的有效方式。
(5)半潜式钻井平台极限强度的研究方兴未艾,以下方面尚待深入研究:实际海洋环境下平台极限承载力分析技术;实际平台结构中的几何缺陷(焊接变形、焊接缺陷);使用工程中的腐蚀、裂纹、工作过程中局部载荷(波浪载荷、设备载荷、事故载荷等)对平台极限强度影响;主甲板生活楼、钻台等结构对整体极限承载力的影响等。
[1] 谢彬.深水半潜式钻井平台设计与建造技术[M].北京:石油工业出版社,2013.
[2] ISO 18072-1-2007,Ships and Marine Technology-Ship Structures Part 1 General Requirements for Their Limit State Assessment[S].International Standard Organization,2007.
[3] ISO 18072-2-Ships and Marine Technology-Ship Structures Part 2 Requirements for Their Ultimate Strength Limit State Assessment[S].International Standard Organization,2007.
[4] IACS.Common Structural Rules for Bulk Carriers[S].2008.
[5] IACS.Common Structural Rules for Double Hull Oil Tankers[S].2008.
[6] ABS.Rules for Building and Classing Steel Vessels [S].2013.
[7] DNV.DNV-OS-C101 Design of Offshore Steel Structures,General(LRFD Method)[S].2011.
[8] Simonsen B C.Ultimate Strength[C]//Proceedings of 15th International Ship and Offshore Structures Congress,2003,San Diego USA.
[9] Wang G.Ultimate strength[C]//Proceedings of 16th International Ship and Offshore Structures Congress,2006,Southampton,UK.2006.
[10] Paik J K.Ultimate strength[C]//Proceedings of 17th International Ship and Offshore Structures Congress,2009,Seoul Korea.2009.
[11] Paik J K,Thayamballi A K.Ultimate Limit State Design of Steel-Plated Structures[M].Chichester,UK:Wiley,2003.
[12] Cyranka C,Viderio P M.Waste oil tank rupture,in Workshop on the Accident with the P-36 Platform,CD ed.[C]//Petrobras and Coppe,2001,Rio de Janeiro,Brazil.2001.
[13] Chakrabarti P,Maiti M K.A simple time domain structural redundancy analysis procedure for semisubmersibles[C]//Proceedings of OMAE 2007,San Diego USA.2007.
[14] Estefen T P,Werneck D S,Estefen S F.Influence of the geometric imperfection on the buckling behavior of floating platform column under axial Load[C]//Proceedings of OMAE 2007,San Diego USA.2007.
[15] 曾常科.半潜式海洋平台结构极限强度研究与分析[D].上海:上海交通大学,2005.
[16] 杨鹏,吴东伟.半潜式平台极限强度计算方法研究[J].船海工程,2011(6):133-137.
[17] 姜峰.基于非线性有限元方法的半潜式平台极限强度研究[D].哈尔滨:哈尔滨工程大学,2010.
[18] 刘昆,张延昌,王自力.基于ABAQUS船体板架极限承载力数值仿真分析[C]//中国造船工程学会学术论文集,2012:189-198.
[19] 刘昆,张延昌.半潜式钻井平台撑杆结构极限承载力数值仿真计算[J].江苏科技大学学报(自然科学版),2012(5):430-433.
[20] 刘昆,张延昌,王自力.深海半潜式钻井平台上部船体极限承载力数值仿真分析[C]//中国钢结构协会海洋钢结构分会学术论文集,2014:224-229.
[21] ABS.ABS Rules for Building and Classing-Mobile Offshore Drilling Units-Part 3-2-Appendix2[S].2008.
[22] Jeom Kee Paik,Bong Ju Kim,Jung Kwan Seo.Methods for ultimate limit state assessment of ships and shipshaped offshore structures-I,II,III [J].Science Drect,2008(2):261-280.
[23] 庄茁.基于ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009.
[24] 彭大炜,张世联.结构极限强度分析的三种有限元解法研究[J].中国海洋平台,2010(2):1-5.
[25] 陈钢,刘应华.结构塑性极限与安定分析理论及工程方法[M].北京,科学出版社,2006.
[26] 张延昌,王自力,王琦,等.半潜式钻井平台管道钢构支架极限强度研究[J] .实验力学,2010(3):339-345.
