任意比工况下基于像素的改进投影矩阵计算方法

王 鹏，汪 敏，戚晓利，冯建有

(安徽工业大学机械工程学院,安徽马鞍山 243032)

任意比工况下基于像素的改进投影矩阵计算方法

王 鹏，汪 敏，戚晓利，冯建有

(安徽工业大学机械工程学院,安徽马鞍山 243032)

针对CT图像重建代数类算法中关键的投影矩阵，提出1种在像素尺寸与探测器间隔为任意比工况下的计算方法。在各投影方向上，根据该比值确定与像素可能相交的最大射线条数，从每个像素出发直接定位到可能与其相交的射线编号，基于射线与像素相交拓扑模型计算的交线长度作为投影矩阵对应元素。利用MATLAB及SNARK09平台仿真验证本文方法的有效性，结果表明：在任意比工况下计算投影矩阵有其实际意义；本文方法能在任意比工况下有效地计算投影矩阵，其效率相对于传统的Siddon方法提高4倍以上；本文方法能有效地应用于SART图像重建算法中。

X射线光学；图像重建；投影矩阵；像素；任意比

X射线计算机断层成像术(X-ray Computerized Tomography,X-CT)因其无损检测的特点广泛用于医学、工业、物探、材料、生物、安全等领域[1-4]，被公认为是20世纪影响人类发展的十大技术之一。X-CT技术图像重建算法根据图像求解出发点的不同可分为矩阵反变换法、解析类算法[5]和代数类算法[6-7]三大类。代数类算法由于数据量巨大等原因，在过去的几十年发展缓慢。近年来，随着计算机技术的快速发展，对巨型数据的处理能力显著提高，代数类算法被重新认可，有关代数类算法的相关研究也成为热点问题。

研究表明[8-9]，代数类算法中，投影矩阵的计算消耗大部分的重建时间，且其计算精度对重建图像质量有相当大的影响，因而该计算成为制约图像快速和高质量重建的瓶颈。为此，很多学者对于投影矩阵计算方法进行了研究[10-13]，但是这些方法都是从单条射线出发，1次计算只能得出该射线相关的投影系数。为此，王旭等[14]提出1种联合代数重建算法(Simultaneous Algebraic Reconstruction Technique，SART)中基于像素的投影系数计算方法，从每个像素出发直接定位到相关射线，随后利用该结果完成投影系数的计算。该方法1次计算可以产生1组射线相关的投影系数，但是其射线定位环节复杂度较高。另外，目前学者们对有关投影矩阵计算方法的研究，采用像素尺寸与检测器间隔相等这一特殊工况，而实际中该比值典型地取为1.4:1[15]，对于更为一般的任意比工况的分析较少。鉴于此，提出1种任意比工况下投影矩阵的快速计算方法并验证其有效性。

1 投影矩阵的计算方法

CT图像重建中，平行束扫描模式下的网格拓扑结构如图1。重建区域由N×N像素(正方形网格)组成，以中心像素的形心为旋转中心建立xOy坐标系，单个像素尺寸为d×d。按从左往右、自下而上的编号原则，各像素可表示为像素 (i,j), i,j=1,…,N，或像素q(q=i+j·N-N)。在投影的M个方向上，有等间距τ的Nd条平行射线穿过重建区域，获得投影数据 pk,k=1,2,…,M·Nd。每组射线沿着投影基准轴x′正向编号为1,2,…,Nd，中心投影射线lO经过坐标原点。则有

其中：xq为像素q的像素值；rkq为投影系数，即为投影矩阵R的第(k,q)个元素的值，用于描述像素q对于投影值pk的贡献度，其大小定义为射线k在像素q中的穿越长度。各种代数类重建算法的求解过程实质上就是对(1)式的数值求解过程。

基于从像素出发的思想，在平行束扫描模式下，提出1种任意比工况下投影矩阵的快速计算方法：根据像素尺寸与探测器间隔之比值确定与任意像素可能相交的最大射线数；随后，在各投影方向上，从每个像素出发，直接定位到可能与该像素相交的射线，基于射线与像素相交的拓扑模型，判断像素与射线的真实相交性，并计算交线长度，将其作为投影系数值；综合各投影方向所得投影矩阵元素，填充为投影矩阵。单投影方向下的计算可以产生该方向下所有射线对于每个像素的投影系数，其过程可以分解为最大可能相交射线数Lmax的预算、射线定位、射线与像素的判交、投影系数计算4步进行。

1.1 最大可能相交射线数的预算

当像素尺寸等于检测器间隔(即d=τ)时，可直观得出，平行射线束中最多有2条射线可能与单个像素相交。在更为一般的两者为任意比工况下，需确定可能相交的射线数。为此引入以下定理。

定理1[16]在二维笛卡尔坐标系内，对于1组不限数量的等距(间距为τ)平行射线束，如果存在1条长度为Z的线段与其垂直相交，那么射线束与线段有或个交点。(分别表示向正、负无穷方向取整，下同。)

平行射线束与单个像素的相交拓扑模型如图2所示，像素ABCD沿着投影方向θ在投影基准轴x′上的投影为线段D′B′，其大小随θ变化

由图2知，平行射束中穿越像素ABCD的射线条数等于平行射束与线段D′B′的交点数。根据定理1，取，则与像素相交的最大射线数目为

1.2 射线定位

1.2.1 最邻近射线定位

根据图1，任意像素(i,j)的坐标位置为

在投影方向θ下，像素(i,j)到中心投影射线的距离S为

α0为像素(i,j)中心到最邻近射线n0的垂直距离。根据式(5)得

将式(7)代入式(6)，得

至此，对于任一像素(i,j)，定位到了最邻近射线n0，并求得两者垂直距离为α0。

1.2.2 可能相交射线定位

定理2[16-17]在二维笛卡尔坐标系内，等间距的1组平行射线束(不限制其数量)与其相互垂直线段的交点，分布在线段中点两侧的数目要么相等，要么相差1(位于线段中点的交点归属左侧)。

根据定理2，若沿着投影基准轴x′方向，在像素中心左右两侧各取相邻近的条投影射线，必能保证所有可能相交射线被选中，同时选取的射线数最少。因此，对任一像素(i,j)，可选择可能相交射线的编号集合{n}为

1.3 射线与像素的判交

确定与像素可能相交的Lmax条射线编号后，需进一步判断其相交真实性。由图2可知，如果射线ln与投影基准轴x′的交点P位于线段D′B′内部，则说明射线ln确实与像素ABCD相交；否则，反之。故射线ln与像素相交的条件是

其中，λ1为线段D′M′的长度，几何意义为像素中心M到经过D(或B)的平行束射线的垂直距离

故对于某一可能相交射线n，判交参数为

至此，对于任一像素，已确定全部与其真实相交的射线编号，即投影矩阵中非零元素的位置。下一步考虑，这些非零元素值大小的计算方法。

1.4 投影系数计算

计算投影系数rkq的一般方法为确定投影射线k与像素q的交点坐标，计算两点之间的距离。由于该方法判断分支过于复杂，重复计算交点坐标和距离导致效率低下，此处根据1.1，1.2节所得数据，采用1种能以较高速率和较少冗余计算射线与像素相交线长度的方法[14]。

以0∘＜θ＜45∘的情况为列，过像素顶点A,C作平行于射线k(EF)的2条辅助线AA′,      C″C′，如图3。设像素ABCD对射线EF的投影系数为r，为像素中心到DD′(或BB′)的垂直距离，为像素中心到C″C′(或AA′)的垂直距离。可知

1)射线EF穿过AC″CA″区域内部时，由ΔADA″得

2)射线EF穿过AC″CA″区域外部时，由图3知

此式仅适用于θ∈(0∘,45∘)⋃(135∘,180∘)的情况。当θ∈[45∘,135∘]且θ≠90∘时，辅助线AA′，C″C′将与网格AD，BC边相交，此时只需将θ的余弦改为正弦sinθ，正弦sinθ改为即可。再综合θ=0∘或90∘的情况，令

可得计算投影系数所需各参数在不同投影角θ的计算方法如表1(其中b为无量纲常数)。由此，投影系数计算公式为

观察表1，参数c2中的α已在射线判交环节中求出，此处可直接引用，无需运算。而其他所有参数，只与当前投影角θ有关，与射线和像素都无关，故每个投影方向下，只需计算1次即可。

表1 相关参数计算Tab.1 Computation of related parameters

2 方法分析

综合以上公式，主要的计算量有S，n0，α0，n，α，Lmax以及θ的三角函数。在某投影角下计算时，投影角θ不变，故有关θ的三角函数和Lmax只需计算1次。n，α分别随着n0，α0而变化，而n0，α0又完全取决于S，故每个投影角下需逐像素计算的只有S。由于在某固定投影角θ下S可以看成是1组行、列成等差的二维数组，故可以采用增量运算进行优化。

本文方法只存储1个投影角下的投影矩阵，不同投影角下的投影矩阵需实时计算。投影矩阵按像素存储，考虑到1个像素内最多穿越Lmax条射线，所以需要O(Lmax·N2)的存储空间存储投影矩阵。同时为了存储与每个像素相交的射线编号，同样需开辟O(Lmax·N2)的存储空间。这样共需的存储空间为O(2Lmax·N2)，由于2Lmax远小于Nd，故本方法所需的存储空间远小于一般方法所需的存储空间O(Nd·N2)。观察所用各公式，各运算的次数见表2。

表2 各种运算的次数Tab.2 Times of various operations

因此1次迭代所需总时间t为

其中，t加，t乘，t取整，t比较分别表示单次加法、乘法、取整和判断比较运算的时间。

3 仿真实验及结果分析

采用仿真实验的方法验证本文方法的意义、快速性与有效性。现实情况与仿真实验之间的差异主要在于是否存在各种真实误差，导致仿真实验结果的质量高于真实情况。但从另一角度而言，仿真实验忽略次要误差因素，更能体现出感兴趣的主要因素。

3.1 验证方法意义

采用SNARK09[18]作为实验平台，测试计算机配置为双核Pentium(R)Dual-Core T4200 2.00 GHz CPU，2 GB DDR内存，Linux操作系统。对像素尺寸与检测器间隔比值分别采用1:1.4，1:1，1:0.714三种工况进行重建分析。选取大小为256×256像素的Sheep-Logan头部模型图像在平行束扫描模式下用滤波反投影(FBP)算法进行重建，为避免投影数据不足对结果的影响，取投影角度数目M=360。重建结果如图4。

观察图4可知，像素尺寸与检测器间隔之比越大，重建图像的空间分辨率越高，然而提高到1: 0.714比值之后质量提升不明显。故可采用1:0.714为近似最佳比值，与实际情况(1.4:1)相符。从更广泛的意思上来说，至少可以确定在不同比值下，图像质量是不同的。由以上可知，讨论任意比工况下投影矩阵的计算方法具有相当大的实际意义。

3.2 验证方法快速性

采用MATLAB 7.11.0作为实验平台，测试计算机配置为4核Intel(R)Core(TM)i3-2100 3.10 GHz CPU，4 GB DDR内存，Win7操作系统。分别用Siddon方法与本文方法计算投影矩阵，取模型大小为N×N, N分别取64，128，256，512像素，平行束扫描模式，投影角度数目M=180,像素宽度与探测器间隔之比d:τ=1.4,单投影角下平行射线数为。每组数据分别用2种方法计算10次，取10次运行时间平均值，结果见表3。

从表3可以看出，本文方法的运行时间不到Siddon方法的1/4，效率明显高于经典Siddon方法。经多次验证，2种方法所生成的投影矩阵在小数点后16位精度范围内仍然完全一致。综合考虑，本文方法优势明显。

3.3 验证方法有效性

为进一步验证本文方法的有效性，将该方法应用于非等比工况下的SART仿真实验中。选用Sheep-Logan头部模型用SART算法进行重建。实验中选取模型大小为256×256像素，平行束扫描模式，像素宽度与探测器间隔之比d:τ=1.4，180个投影角，每个投影下359条射线。像素初值为0，松弛因子为0.1，分别迭代1，2，3次，结果如图5。

由图5可看出，与原始模型相比，重建效果理想，经过1次迭代就出现了原始图像中所有特征，经过3次迭代后就非常接近原始图像。说明本文方法可完全有效应用于SART图像重建算法。

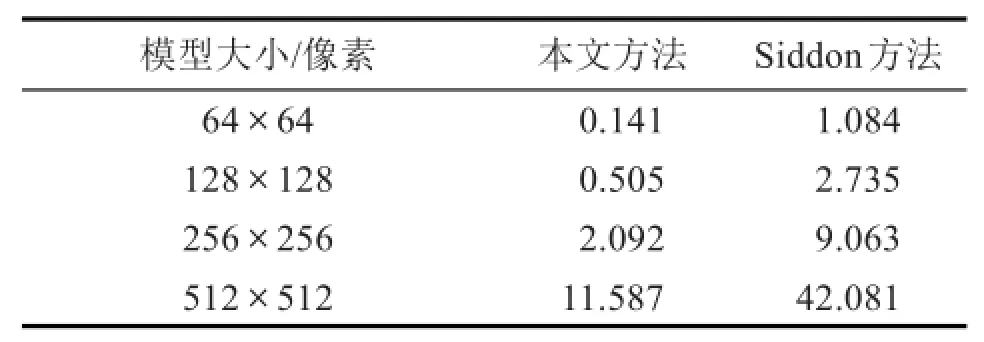
表3 不同模型尺寸下2种方法的运行时间/sTab.3 Computing time in different mode sizes/s

4 结 论

提出了1种在任意比工况下能有效计算投影矩阵的方法，从推导过程及仿真实验结果可知：

1)本文方法能在任意比工况计算投影矩阵，并有效运用于SART图像重建算法；

2)本文方法所需的存储空间为O(2Lmax·N2)，远小于一般方法所需的存储空间O(Nd·N2)，空间效率大幅提高；

3)在常规模型尺寸下，本文方法的运行时间不到Siddon方法的1/4，时间效率提高4倍以上。

为进一步提高其运算效率，下一步将考虑加入增量运算的方法；由于方法局限于平行束投影模型，对于扇束及三维锥束投影模型还需改进。

[1]Goldman L W.Principles of CT and CT technology[J].Journal of Nuclear Medicine Technology,2007,35(3):115-128.

[2]汪敏.同步辐射CT技术研究及应用[D].合肥：中国科学技术大学，2006.

[3]汪敏，胡小方，伍小平.物体内部三维位移场分析的数字图像相关方法[J].物理学报，2006,55(10):5135-5139.

[4]陆常周.CT的数学处理方法及其新价值[J].安徽大学学报：自然科学版，1980,4(2):69-75.

[5]Lewitt R M.Reconstruction algorithms:transform methods[J].Proc IEEE,1983,71(3):390-408.

[6]Herman G T.Fundamentals of Computerized Tomography:Image Reconstruction from Projections[M].4th ed.New York: Springer,2009:191-216.

[7]Censor Y.Finite series-expansion reconstruction methods[J].Proc IEEE,1983,71(3):409-419.

[8]庄天戈.CT原理与算法[M].上海：上海交通大学出版社，1992:77-98.

[9]曾更生.医学图像重建入门[M].北京：高等教育出版社,2009:125-190.

[10]Robert L S.Fast calculation of the exact radiological path for a three-dimensional CT array[J].Medical Physics,1985,12(2): 252-255.

[11]周斌，王连堂，王俊杰，等.代数重建算法中一种快速投影系数计算方法[J].计算机工程与应用，2008,44(25):46-48.

[12]张顺利，张定华，赵歆波.代数重建算法中一种快速投影系数计算方法[J].计算机应用研究，2006,24(5):38-40.

[13]陈洪磊，贺建峰，刘俊卿.基于二维检索的投影矩阵算法[J].计算机工程，2013,39(2):229-232.

[14]王旭，陈志强，熊华，等.联合代数重建算法中基于像素的投影计算方法[J].核电子学与探测技术，2005,25(6):785-788.

[15]Coric S,Leeser M,Miller E,et al.Parallel-beam backprojection:An FPGA implementation optimized for medical imaging[C]//Proceedings of the 2002 ACM/SIGDA Tenth International Symposium on Field-programmable Gate Arrays.New York: ACM,2002:217-226.

[16]郑崇友，王汇淳.几何学引论[M].北京：高等教育出版社，2005:55-64.

[17]王培珍，许睿.任意多边形填充新算法[J].安徽工业大学学报：自然科学版，2009,26(4):405-408.

[18]Klukowska J,Davidi R,Herman G T.SNARK09-A software package for reconstruction of 2D images from 1D projections[J].Computer Methods and Programs in Biomedicine,2013,110(3):424-440.

责任编辑：何莉

Improved Projection Matrix Computation Method Based on Pixel under the Working Condition with anArbitrary Radio

WANG Peng,WANG Min,QI Xiaoli,FENG Jianyou (School of Mechanical Engineering,Anhui University of Technology,Ma'anshan 243032,China)

For the project matrix which is critical in CT image algebraic reconstruction algorithms,a computation method for dealing with an arbitrary pixel-size to detector-spacing ratio case was presented.In each projection direction,the maximum number of the lines that may intersect a pixel was determined according to the ratio,and then the lines were located based on each pixel,and finally intersection lengths were computed to be assigned to the related project matrix elements according to the intersection topological model.MATLAB and SNARK09 software platforms were employed for simulation experiments to justify effectiveness of the method.Results show it is significant to compute the project matrix in the arbitrary ratio case,and that in the arbitrary ratio working condition a projection matrix can be effectively computed by the method,which is four times efficient than the classical Siddon algorithm,and that the method could be effectively used in SART image reconstruction algorithms.

X-ray optics;image reconstruction;projection matrix;pixel;arbitrary ratio

434.19；TN319.75

A

10.3969/j.issn.1671-7872.2015.02.013

2015-01-06

国家自然科学基金面上项目(11372138);安徽高校省级自然科学研究项目(KJ2013Z021)

王鹏(1989-)，男，安徽东至人，硕士生，主要研究方向为二维CT重建算法。

汪敏(1979-)，男，安徽枞阳人，博士，教授，主要研究领域为光学无损检测技术与应用。

1671-7872(2015)-02-0157-06