新型功率放大器PLTC行为模型及预失真应用

高明明，南敬昌，刘 月

(辽宁工程技术大学电子与信息工程学院，辽宁葫芦岛125105)

1 概述

无线通信正朝着多载波、多电平、宽频带和高频谱效率方向高速发展，但是也伴随着信号的峰均比不断增高，这会使得无线系统中最核心的器件功率放大器进入非线性区，功率放大器在这种情况下将产生记忆效应和强非线性，使系统有效带宽下降，影响功率放大器的附加效率。正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)是一种高速率的多载波传输技术，利用多个彼此正交的子载波并行传输数据，最大程度利用频谱资源，具有优异的抗噪声性能和对抗多径衰落的能力［1-3］，是4G或B3G的关键技术之一。但是OFDM当其载波的相位在某一时刻达到一致时，它的峰均比会很高，使得功率放大器非线性效应对OFDM信号的影响十分严重，从而产生带外谱扩展和带内失真。带内失真降低系统性能，出现互调分量，带外谱扩展则导致邻近信道干扰。因此为了减小系统对信号的峰均比的要求，补偿功率放大器的非线性，可以通过功放线性化技术来改善系统总体的优化设计［4-5］。

功率放大器的行为建模是非常重要的，经常作为分析功放性能的第一步，也为数字预失真技术提供必要的模型基础。对具有记忆效应的非线性功率放大器建立精准的行为模型是现在研究的热点问题，把建立的功放行为模型应用于预失真器模型，有助于提高预失真系统的性能及线性度，具有重大的理论实践参考价值。有对于记忆预失真技术的关键就是在于描述功放的逆特性而选择的非线性模型。

有很多功放行为模型被提出，一般有神经网络模型和Volterra模型。Volterra级数的模型参数数量随非线性和记忆深度的增加呈指数形式增长，虽然可以很好地描述非线性系统的物理意义，但是模型的复杂性导致系统参数辨识复杂［6］;模型的记忆效应表征精度低，直接影响了预失真器的线性化性能。因此很多Volterra模型的建立并没有考虑到功放记忆效应的问题。很多文献提出了简化的Volterra模型，多项式模型(Model of Polynomial，MP)［7］，一般多项式模型(GeneralModelofPolynomial，GMP)［8］，包 络 多 项 式 模 型 (Envelope Model of Polynomial，EMP)［9］、正交多项式模型［10］以及一些两箱模型。这些两箱模型如Hammerstein模型分裂增强型 Hammerstein模型、PLME模型、增强型Hammerstein模型、双非线性双箱模型(TNTB)，以及Winer模型、LMEC模型等。

本文提出一种新型精确简化的三箱模型PLTC(parallel-LT-TMP-CIMT)，并用于带有记忆效应的非线性功率放大器行为建模及预失真。该模型由查找表(Look-up Table，LUT)、三角记忆多项式(Triangular Memory Polynomial，TMP)［8］和记忆时刻信号交叉项并联构成。PLTC模型在行为模型和预失真中的性能是使用16QAM信号驱动一个强非线性大功率Doherty功率放大器来验证所提模型的性能。同时将新模型的性能与GMP模型、MP模型、PLME模型以及LMEC模型进行全面的比较，即通过对各种模型的NMSE、EPSD，以及系数数量进行的比较。

2 PLTC行为模型描述

PLTC模型是一个三箱模型，由3个非线性子模型并联而成。由高阶无记忆高阶非线性函数、低阶记忆多项式以及记忆时刻信号交叉项CIMT函数组成，先后处理了强静态非线性和动态非线性。PLTC模型的结构如图1所示。PLTC模型通过引入当前信号与其滞后包络项之间的交叉项，获得更高的准确度，并通过增加查找表单元来表征静态强非线性，降低了记忆多项式子模型和包络记忆多项式子模型中对非线性的阶数要求，从而降低了整个模型的复杂度。由于在PLTC模型中，包含了同一时刻信号的交叉项、当前时刻与记忆时刻的交叉项以及记忆时刻信号间的交叉项三部分，因此，更加符合实际功放的非线性特性和记忆效应特性，适用于宽带功率放大器的建模。

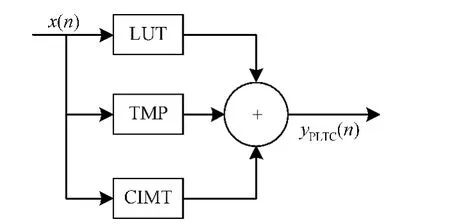
图1 PLTC模型框图

第1个子模型采用无记忆高阶非线性函数，可以用查找表结构来实现。其数学表达式为:

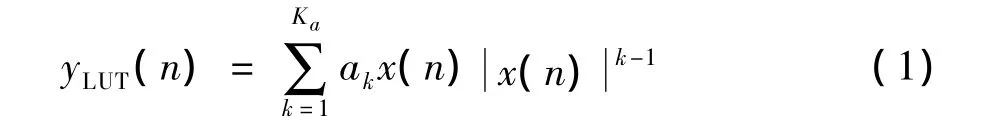
其中，x和y分别为第1个子模型的输入和输出信号;Ka表示非线性阶数;ak表示第1个子模型的参数。

第2个子模型三角多项式(TMP)函数，描述无线通信系统中功放的非线性可以用离散有限记忆复基带Volterra级数来表示，定义公式如下:

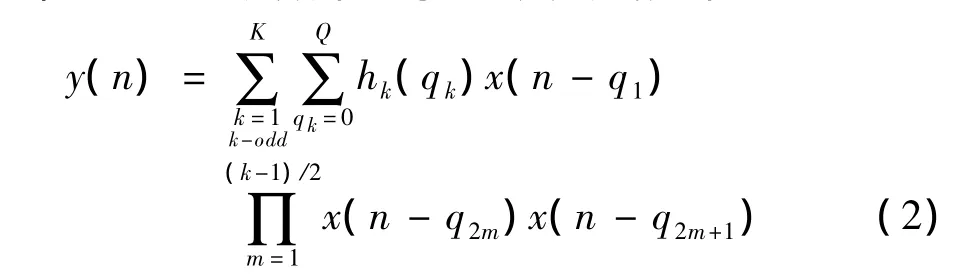
其中，x(n)和y(n)为系统的输入和输出;K为非线性阶数;Qk为记忆深度;hk(qk)为k阶Volterra核;qk由整数值延迟组成;对所有的 k=1，3，…，K有qk=0，1，…，Qk。庞大的系数数量使得 Volterra级数难以在实际中得到应用，因此在实际建模和DPD中常采用简化的Volterra级数模型。

多项式模型(MP)为简化了的Volterra级数模型。其输入x(n)，输出y(n)可表示为:

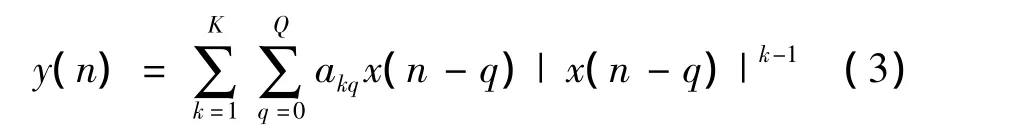
其中，k是非线性阶数;q是记忆深度;x(n)和y(n)分别为多项式的输入信号和输出信号。在式(1)中，x(n－q)的k阶多项式表征，akq为MP模型系数。最大非线性阶数对输入来说一般是恒定的。在基于OFDM无线宽带通信系统中，当长期记忆效应被考虑进来的时候，最大记忆阶数会比较大，这导致了大量系数的产生并提高了计算的复杂性。但由于在实际的实践观察中得知非线性动态效应会随着记忆阶数增加而逐渐减小，因此可以试着调整过去输入的最大非线性阶数在保持功放预失真性能的同时降低其系数数量。K=N，N定义如下:

那么式(3)变成:

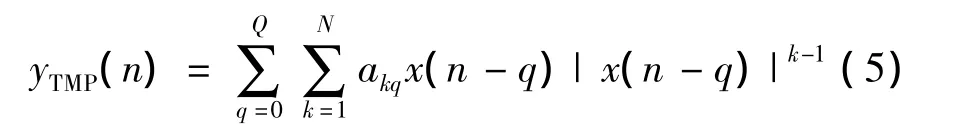
N为最大非线性阶数时，Q是最大记忆深度。在式(4)中，最大非线性阶数N是不连续的，是随着记忆深度而变化的。把式(5)称为TMP模型。在TMP模型中是Volterra模型的一种简化形式，它只考虑Volterra核函数中对角线的值，其他均忽略不计，这样模型中系数会随记忆深度和非线性阶数呈指数增长的问题就会被很好地解决［6］，可以使得系统随非线性阶数和记忆深度呈线性增长的关系［8］。

考虑到PLTC模型中查找表(LUT)表征了静态非线性，因此TMP模型不包括无记忆项，q从1开始取值。TMP增加了历史时刻包络对当前输入信号的影响项。

第3个子模型采用记忆时刻信号交叉项CIMT函数表示，其数学表达式为:

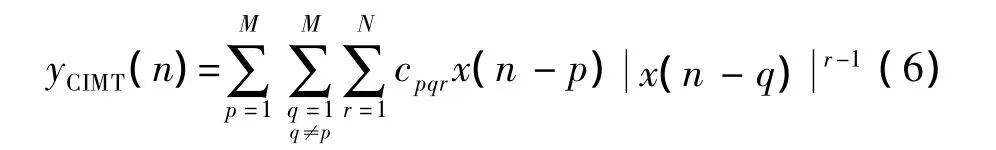
其中，CIMT子模型的输出和输入信号分别用y和x表示;CIMT子模型的交叉项的阶数和交叉记忆深度分别用N和M表示;cpqr为CIMT模型的系数。记忆时刻的信号之间的高阶非线性项对系统的影响较小，而且在模型各项中，阶数增加会导致模型系数量的快速增长，大大增大了复杂性，所以本模型只考虑记忆时刻信号间的三阶交调量，对系统影响较大的令式(3)中的r=3，式(3)化简为:

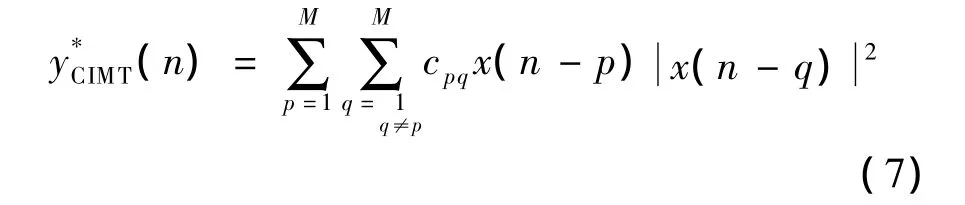
将式(1)、式(6)和式(7)相加，构成了新型PLTC模型，PLTC模型的数学表达式为:

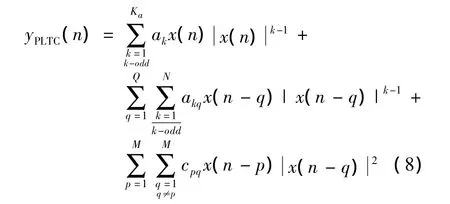
此模型避免了串联形式下每个子模型需要同时选择同样非线性阶数的问题，各项非线性阶数相同会导致模型尺寸太大而增加模型计算的复杂度，因此PLTC模型需要通过一些方法来减小模型尺寸，通过添加并联非线性子模型来解决。LT项表征了功率放大器的高阶静态非线性行为，TMP的子模型表征了功率放大器的低阶非线性并控制了模型的尺寸，使总系数个数变得合理［11-14］。TMP增加了历史时刻包络对当前输入信号的影响项。CIMT函数增加了记忆时刻信号交叉项。

3 PLTC模型的辨识

PLTC模型中LT，TMP和CIMT子模型可以彼此独立地设置其非线性阶数和记忆深度来提升整体模型的性能，如果按照习惯的方法会同时对这些子模型的记忆深度和非线性参数进行扫描，这样就会得到大量不合理的组合，并增加了计算量。因此，必须采取分步的方法进行系数的确定。这样既能提高模型的性能，又使得计算复杂度没有明显的增加。

PLTC模型的辨识分为3步。首先利用被测功放的输入输出数据完成无记忆高阶静态非线性子模块的参数辨识，其次将功放的输入输出数据向下嵌入到TMP子模型中进行参数识别，最后对CIMT子模型中参数完成识别。

TMP子模型与CIMT子模型可同步辨识，首先令:

其中，Y是2个动态非线性多项式子模型的输出向量;X为基于2个多项式基函数与输入信号构成的矩阵。A是包含了TMP子模型与CIMT子模型系数的向量。矩阵X被定义为:

其中，XTMP和XCIMT分别为TMP与CIMT基函数构造的子矩阵。

其中，j以扫描方式从0～MCIMT;i以扫描方式从0到NCIMT。

最后，用最小二乘法法进行拟合，求得A为:

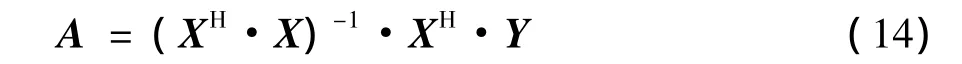
其中，［·］H为共轭转置。

是否能增强模型的整体性能和选取适当的模型系数是PLTC模型的子模型尺寸的选取所要权衡的两方面。模型精确度用归一化均方误差(Normalized Mean Square Error，NMSE)指标来衡量。模型尺寸一般选取能得到更小的归一化均方误差值以及对应组合产生系数最少的值。子模型尺寸的确定用一般的扫描方法。

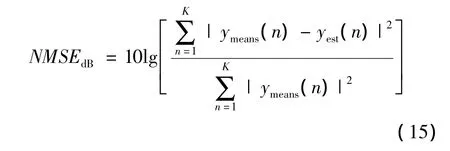
其中，ymeans为实际测量的功放输出波形;yest为模型的输出波形;K是输出波形样本的数量。

首先完成无记忆高阶静态非线性子模块的参数辨识，对LT的非线性阶数进行扫描，从1～17。然后，TMP子模型参数的确定是用足够大范围的扫描模型同时对TMP子模型的非线性阶数和记忆深度进行扫描的。记忆深度扫描从0～5，非线性阶数从0～15。TMP子模型中最大非线性阶数是不连续的，是随着记忆深度而变化的，忽略偶次项就克服了传统最大记忆阶数会比较大而导致的大量系数的产生并提高了计算复杂性的问题。

TMP模型的参数被确定时，CIMT子模型也在第三步被确定，CIMT子模型参数也同时在足够大范围扫描。对应每次迭代，TMP子模型和CIMT子模型系数同时确定，如同式(9)～式(14)描述。子模型的准确性是使用NMSE量化的指标，最后子模型参数选择产生系数最少，达到最低NMSE的对应组合。

在分别对各个子模型进行系数选取时，有时可以获得最佳NMSE值的组合会使系数数量变得很高，因此，非线性阶数和记忆深度组合的选取要兼顾计算量的复杂性以及模型的精确度，要从中选取一个合适的方案。

最后确定LT的非线性阶数为11，TMP子模型的记忆深度和非线性阶数分别为7和5，忽略偶次项。CIMT子模型的记忆深度为3。PLTC模型的总系数个数是25，模型的NMSE值为－37．22 dB。

4 模型性能评估及验证

为了验证PLTC模型的性能，利用矢量信号发生器(N5182A)、高功率 LDMOS Doherty功率放大器、频谱分析仪(PXA N9030A)、衰减器搭建测试平台，如图2所示。采用16QAM信号作为输入信号。被测功放的中心频率是 1．96 GHz，增益为50 dB。

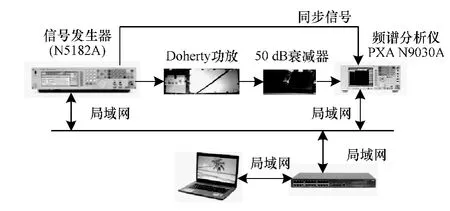
图2 实际测试平台

PLTC模型由于Ka，K，Q和M值的选择直接影响模型的精确度，对这4个参数同时进行扫描会得到大量不合理的组合，提升了计算量，因此首先估计无记忆非线性子模型LT的参数Ka。利用采集到的数据建立无记忆非线性模型，非线性阶数从1扫描到17，图3显示了对应不同Ka值时的NMSE。从图3可以看出，随着非线性阶数的增加，模型的精确度也随之升高，但同时伴随着系数的增加。为兼顾模型精确度和复杂度两方面因素，选择Ka=11作为无记忆非线性子模型的参数。

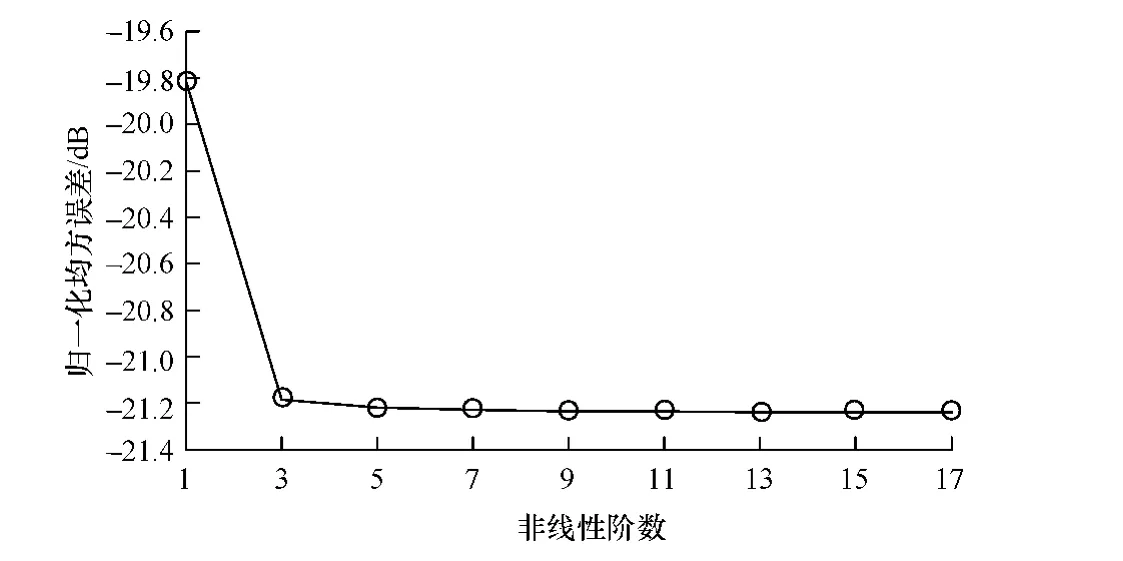
图3 归一化均方误差性能曲线

射频功率放大器中带有记忆效应的输入分量阶数越高，对输出的影响越小，记忆效应随着时间变长而减弱，因此TMP子模型的非线性阶数K可以适当降低，选取合理的值。对非线性阶数从0扫描到15，记忆深度Q从0扫描到5。在时域中，功放模型的精确程度用归一化均方误差(Normalized Mean Square Error，NMSE)指标来衡量［15］。图4 利用三维立体图展示了对应不同K和Q值时的NMSE值，K=11时，NMSE为–21．236 2。从图4中可以看到，随着模型非线性阶数与记忆深度的增加，文中所建立模型的精度逐渐提高。对射频功率放大器进行建模时，必须合理地选取非线性阶数K和记忆深度Q，结合较少的系数与较小的NMSE值综合决定系数的取值。非线性阶数和记忆深度的增加会使模型的准确度得以提升，但模型系数的数量也大大增加了。因此，TMP模型选取K=7，Q=5。忽略偶次项，大幅降低了模型的复杂性。为进一步降低PLTC模型的复杂度，令CIMT子模型中的M=3。

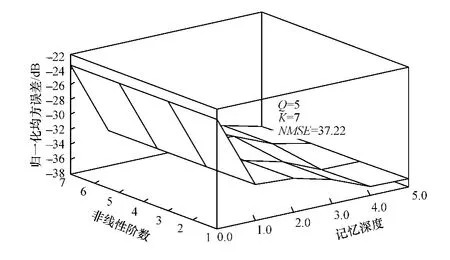
图4 归一化均方误差性能三维立体图

PLTC模型最终选定LT子模型的非线性阶数为11，TMP子模型的记忆深度和非线性阶数分别为7，5，CIMT子模型的记忆深度为3。其中，LT子模型系数为11，TMP模型的参数为K=7，Q=5，忽略偶次项，共8个系数，CIMT子模型系数为6。合计共25个参数。因此，PLTC模型的总系数个数是25，模型的 NMSE值为 －37．22 dB。表1为 PLTC模型与多项式模型 MP、一般多项式模型 GMP、LMEC模型的总系数与NMSE的对比。

表1 不同模型NMSE与总系数比较

图5为利用LPTC模型作为预失真器对功放进行数字预失真前后的输入输出幅度特性曲线。可以看出，经数字预失真后的输入输出幅度特性曲线得到显著改善，基本上形成一条直线，可以满足系统要求。

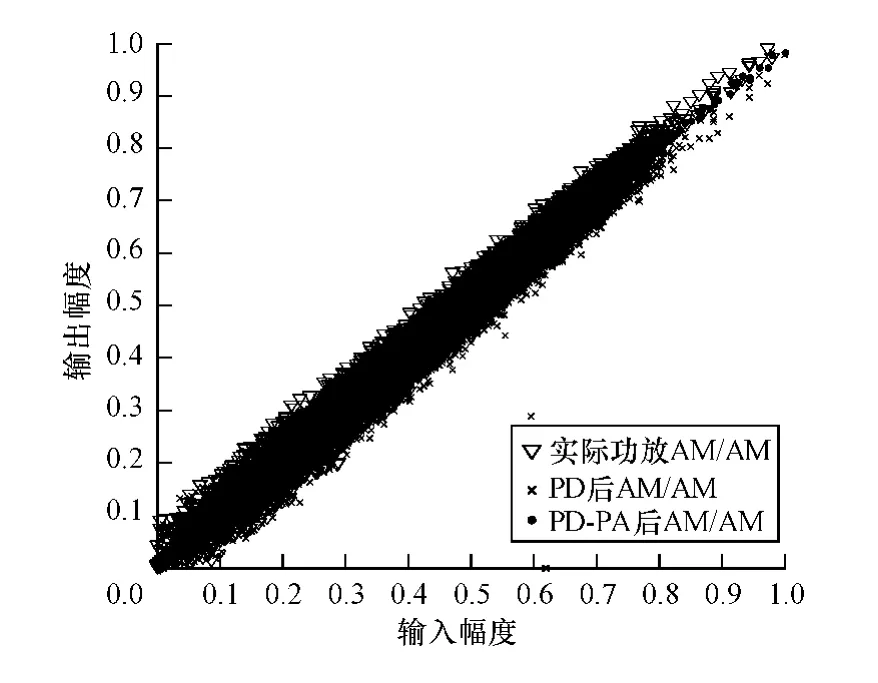
图5 输入输出幅度特性曲线

在数字预失真技术中，所使用功率放大器行为模型的准确度越高，则仿真可以得到的预失真效果就越接近实际中的情况，将PLTC模型应用到数字预失真系统中，同时与MP模型、GMP模型和LMEC模型的预失真性能进行比较。图6为使用16QAM信号时，使用3种模型进行数字预失真前后的功率谱密度。

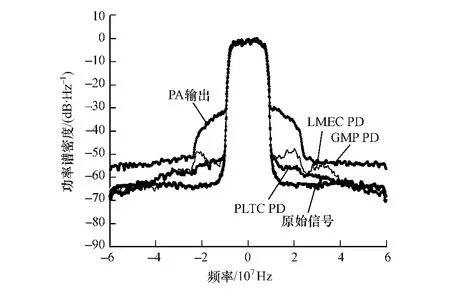
图6 3种预失真方法性能比较

利用实际测试平台来验证PLTC预失真方法的实际线性化效果。对原始的输入信号采用PLTC方法构建预失真器，数字预失真前后功率放大器输出信号的PLTC对比如图7和图8所示，可以看出，经过PLTC预失真方法后，ACPR有大约22 dB的改善，说明该方法能够有效地对功放进行线性化。

图7 无预失真时功放输出信号的ACPR值

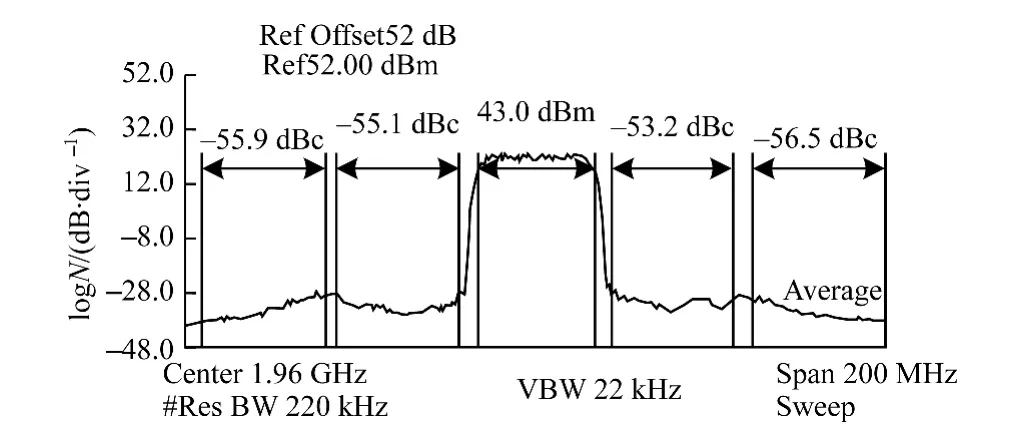
图8 有预失真时功放输出信号的ACPR值

5 结束语

本文针对功率放大器的记忆效应和非线性特征提出了PLTC模型。PLTC模型用于功率放大器的行为模型建模以及数字预失真的应用，该模型是简化的三箱模型，由查找表、三角记忆多项式和记忆时刻信号交叉项并联构成。使用16QAM信号驱动一个强非线性大功率Doherty功率放大器来验证所提模型的性能。实验结果表明，与 MP模型相比，PLTC模型的NMSE改善了3．02 dB，系数量节省了65%;与 GMP模型相比，PLTC模型的 NMSE与GMP和LMEC模型的NMSE相差不大，但是其系数量大大降低，比 GMP模型系数节省了75%;比LMEC模型系数节省了50%。对原始的输入信号采用PLTC方法构建预失真器，经过PLTC预失真方法后，ACPR有大约22 dB的改善，说明该方法能够有效地对功放进行线性化。

［1］ Kwan A，Hammi O，Helaoue M，et al．High Performance Wideband DigitalPredistortion Platform for 3G +Applications with Better than 55dBc over 40 MHz Bandwidth［C］//Proceedings of IEEE MTT-S International Microwave Symposium．Piscataway，SA:IEEE Press，2010:1082-1085．

［2］ Roblin P，Keun S，Chaillot D M，et al．Frequencyselective Predistortion Linearization of RF Power Amplifiers［J］．IEEE Transactions on Microwave Theory and Techniques，2008，56(1):65-76．

［3］ Sung C J，Hammi O， Ghannouchi F M． Design Optimization and DPD Linearization of GaN-based nsymmetrical Doherty Power Amplifiers for 3Gmulticarrier Applications［J］．IEEE Transactions on Microwave Theory and Techniques，2009，57(9):2105-2113．

［4］ 吴 静．OFDM系统中的预失真技术研究［D］．西安:西安电子科技大学，2008．

［5］ 李 波．无线通信中射频功率放大器预失真技术研究［D］．西安:西安电子科技大学，2009．

［6］ 廖 意，苏东林，吴 琦，等．基于Volterra级数的功放行为模型建模与简化［J］．北京航空航天大学学报，2013，39(7):990-994．

［7］ Hammi O，Ghannouchi F M，Vassilakis B．A Compact Envelope Memory PolynomialforRF Transmitters Modeling with Application to Baseband and RF-digital Predistortion［J］．IEEE Microwave and Wireless Components Letters，2008，18(5):359-361．

［8］ Yu Cuiping，Liu Yuan’an，Du Tianjiao，et al．New Predistorter sing Triangular Memory Polynomial for Power Amplifier of OFDM-based Wireless Broadband Communication System［J］．The Journal of China niversities of Posts and Telecommunications，2012，19(2):43-47．

［9］ Morgan D R，Ma Zhengxiang，Kim J，et al．A Generalized Memory Polynomial Model for Digital Predistortion of RF Power Amplifiers［J］．IEEE Transactionson Signal Processing，2006，54(10):3852-3860．

［10］ 佀秀杰，金明录．一种新的用于Hammerstein预失真器的自适应结构［J］．电子与信息学报，2011，33(6):1345-1349．

［11］ Younes M，Hammi O．An Accurate Complexity-reduced“PLME”Model for Behavioral Modeling and Digital Predistortion ofRF PowerAmplifiers［J］．IEEE Transactions on Industrial Electronics，2011，58(4):1397-1405．

［12］ 曹新容，黄联芬，赵毅峰．一种基于Hammerstein模型的数字预失真算法［J］．厦门大学学报:自然科学版，2009，48(1):47-50．

［13］ Hammi O，Ghannouchi F M．Twin Nonlinear Two-box Models for Power Amplifiers and Transmitters Exhibiting Memory Effects with Application to Digital Predistortion［J］．IEEE Microwave and Wireless Components Letters，2009，19(8):530-532．

［14］ Ding Lei，Morgan D R，Ma Zhengxiang，et al．A Robust Digital Baseband Predistorter Constructed sing Memory Polynomials［J］．IEEE Transactions on Communications，2004，52(1):159-165．

［15］ 金 哲，宋执环，何加铭．基于简化Volterra级数的射频功率放大器建模与辨识［J］．电路与系统学报，2008，13(5):90-94．