基于小波变换频谱细化方案的电动机故障检测方法

陈庆协，吴春富，陈晶晶

（龙岩学院 物理与机电工程学院，福建 龙岩 364012）

电动机出现故障时，通常会发出故障信号，目前故障信号的处理有很多种方法，如神经网络，模糊神经网络处理和小波变换等.本文针对交流感应电动机的常见故障，提出了基于小波变换理论和独立分量理论的故障检测和诊断方法，以检测到的交流感应电动机定子电流为实验数据，对交流感应电动机定子正常和故障电流信号进行检测、分析和比较.信号噪声是故障检测人员判断、评价信号是否处于常态的唯一标准，通过小波变换，采用阈值法消除信号的高频噪声干扰，提高信号的信噪比，然后通过独立分量分析方法，提取出各信号特征，进而在短时间内判断出故障的发生地点和具体类型.实践证明，小波变换频谱在电动机故障检测方面的应用效果是可行的.

1 转子故障成因及电流故障分量特点

机械故障、电气故障是电动机常见的两种故障类型，机械故障是因轴承、机械、齿轮等零件工作出错而造成的；电气故障是因电压不对称、电动机负载不平衡、定子绕组不良、转子故障等原因.因本文篇幅有限，笔者主要研究转子部分故障成因，从电流故障分量特点入手，解读交流感应电动机常用转子类型与具体实现状况.

1.1 转子故障成因

转子也被称为“笼型转子”，由转子铁心、转子绕组、转轴三部分构成，铁心套在转轴上，与转子绕组协同工作，是电动机电磁路线的中枢，绕组内的铜条依靠电导线连接，在运行时，可瞬时传播电流、电磁感应，具体结构如图1.

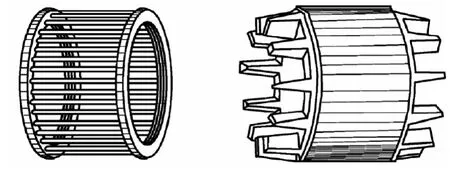
图1 交感电动机内转子形状

电动机转子导条、转子叠片以及转子端环受破损，被损坏或出现功能障碍时，转子导条会因受强大压力而断裂、导热能力急速下降，甚至于丧失.再加上电动机自我散热能力不足，长时间超负荷运转，会使电流产生的热应力持续上升，转子、转子周围的相关机械结构会承受巨大机械应力，到达临界值后，端环焊接处也会相继断裂，致使电动机出现重大运营故障.

1.2 电流故障分量特点

电动机正常运行下，定子电流只含有基波分量,频率为f1，转子电流频率为sf1.当出现转子故障时，转子电流的变化值会失去周期性特征，电流频率也会变得不对称、不规律的.经试验检测，定子的电流频率始终是恒定的，为(1±2s)f1，这一部分电流转嫁给转子的电流分量是相等的，但由于转子结构受故障影响而变得不稳定，所以其电流分量也不固定，总之发生变化.在故障检测时，检测人员经常利用转子电流分量值不一定这个特征，校验转子运行是否正常，如果其频率与基波频率f1接近，如电动机运行状态较为稳定，那么说明转子的结构并没有受到强力破坏，电流分量变化不会太大，上升、下降幅度在2%-4%范围内；如果定子基波频率为50Hz，那么(1-2s)转子电流分量也会与之相对，在48-49.5Hz范围内超出范围，说明转子电流频率下降，信号传播受阻，生产能力下降.

2 重采样的必要性

重采样是指一类象元的信息内插出另一类象元信息的过程，在交感电流电动机故障检测中，能从高分辨率感影像中提取出低分辨率影响，所以该检测操作是十分必要的，具体操作方法如下.

模拟电动机转子导条故障、轴承故障等状态，通电状态下，再加三组单极变压器，配套安装电压表，测量电子、转子的电压，不同变压器显示的相位电压不同.检测人员使用电流探针，来检测电子电流，在透过定子电流确定转子电流频率分量，搜集、统计“故障信息”，最后，利用重采样步骤，将频谱细化，抽样间隔取m△t（m为细化倍数、△t为原采样间隔），重采样长度N始终不变.同时，为了精准计算重采样信号的规律和故障特征，检测人员有时也会进行FFT变换，得到固定区段内fL-fH的细化频谱，倍数也可以根据需要来选择.此外，重采样采集的电流信号大多为仿真数据，如果将其列为故障信号的主要说明数据并不十分科学，所以在样本采集时，必须先对高频电流分量等数据进行消噪处理，尽可能依靠独立分量绘制故障特征分布图，如此总结出来的故障情况更加准确、有效.

3 小波理论优异性

小波变换的理论是近年来兴起的新的数学分支，它是继1822年法国人傅立叶提出傅立叶变换之后又一里程碑式的发展，解决了很多傅立叶变换不能解决的困难问题.在信号处理领域，傅立叶变换理论与小波变换理论有着同样的优异性.在本文论题中，电动机的故障检测更适用于小波理论，原因有三，一是，小波变换能够保存原有函数的具象表现，在此基础上加用族基函数，得来的函数能够有足够的空间修改、伸缩，更贴近于原始故障信号；二是，小波变换理论在处理不同空间、不同频率的子图像时，它能够进行多分辨率分析，并将所有结果储存在一起，组合成分量压缩包，供人挑选；三是，根据S.Mallat的塔式分解算法，图象经过小波变换后被分割成四个频带：水平、垂直、对角线和低频，低频部分还可以继续分解，而傅立叶变换理论则无法支撑进一步的信号处理任务.由此可见，小波理论的优异性特征明显，无论是那一形式、区间的信号，都能够透过小波变换，加以修饰、处理，准确为故障检测人员提供数据信息，且信号的敏感度也非常强，稍有偏差，信号函数、翻译数据马上会做出“警示”反应，显示问题.从小波理论的优异性上看，小波变换、小波变换理论、不同种类的计算方式都是为信号故障检测而服务的，原始信号的变化特征才是小波变换对应频谱细化操作的根本诉求.

4 小波变换及对应频谱细化分析

上文提到，小波变换理论是支持对应频谱细化的，且细化倍数很高，在实践过程中，不同操作步骤，涉及到不同操作办法，笔者将结合小波对信号x(t)的变换形式，研究小波变换及对应频谱细化分析，公式与具体步骤如下：

变换公式：W(t)=x(t)*Ψg(t)

4.1 滤波

选择特定的频带区间，fL-fH范围内信号的基本组成成分，即为W(t)，在进行小波变换时，必须将参数调整到规定值内（L-H），即为参数a.小波变换之后，各变换后的滤波应共同储存在资料库中，△f=fH-fL，△f满足电动机正常运行状态下的电流频率说明滤波特性稳定，如不满足，说明小波变换过程中，对应频谱发生了偏移，滤波性质发生了改变.

4.2 频移

滤波后，W(t)×移频因子，促使频谱信号向需要的方向移动，以测试不同滤波性质的对应频谱，但这种频移处理是有一定限制的，与频谱细化的倍数有直接关系，频谱细化倍数不高，则频移距离也不能过大，反之，频移距离可以相应扩大.

4.3 重采样

重采样与上文提到的理论概念大体相当，在小波变换中，重采样是频谱细化中的重要环节，抽样间隔根据频谱的变化区间而定，间隔一般以m△t来表示，m为细化倍数，△t表示采样区间之间的频谱间隔.在处理小波变换对应频谱时一定要注意，采样数据的长度是恒定不变的，通常为N.

4.4 信号转换

小波变换后，还应对重采样的信号进行FFT变换，得到固定区段内fL-fH的细化频谱，倍数也可以根据需要来选择.从现实应用的滤波器设计结构上看，FFT变换直接关系到滤波器的滤波效果，只要把握好滤波特性，小波变换的仿真程度就会大大提升，反之，重采样的信号会失真，无法表示具体的故障信号，故障检测人员也就很难以此为依据，推断出故障问题所在了.

5 在电机故障检测过程中的主要应用

随着现代工业生产规模的逐步扩大，以电动机为核心的生产装置其设计结构愈加复杂，为了提升各生产单元的生产效率，降低电动机故障，修缮故障维修工作.各大工程纷纷引入了小波变换的频谱细化方案，将其应用在电动机故障检测方面，得到良好应用，具体案例如下（如图2）：

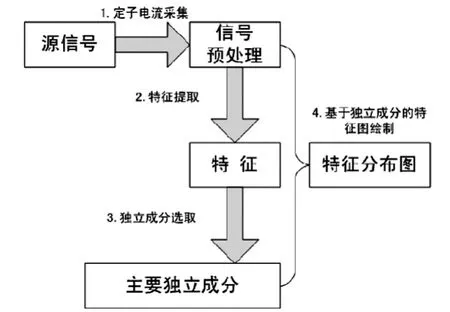
图2 小波变换的频谱细化方案应用于电动机故障检测时的操作流程

5.1 快速傅里叶变换

傅里叶变换本身也存在不足，所以当小波转换是，有限长、快速衰减的母小波的振荡波形并不稳定，组合而成的信号属于非稳态信号.尤其是在频谱细化方案当中，要准确截取固定时域中的信号，必须严格按照傅里叶变换定义，进行小波变换，公式如下：

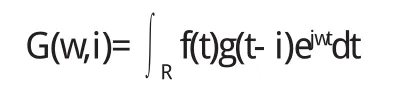
其中，g(t-i)属于窗函数，i为可变参数，在一段时间内，变动i可控制函数大小值变化，进而通过应设函数显示出“逐段图像”——f(t)，这个图像可以表现出小波在特定频率区段内的电流分量值.

在本次操作中，重采样信号的频率为256Hz，数据长度为256点，有效频率范围在0-128Hz之间，将上述数值引入FFT计算公式可知，小波变换后，实践操作得出的频率分辨率为1Hz，电流频率分量值为(1±2s)f1.快速傅里叶变换是为后续小波变换提供信息依据，因为两种理论在频谱处理方面有较大差异，所以为了保证故障检测的稳定性，通常情况下，故障检测人员都会先做快速傅里叶变换，得到具体、真实值后，再计算小波变换值，对比研究之后，再分析故障问题.

5.2 小波变换

5.2.1 构造组合小波

还是选择上文实验案例，经检测，f1=37.5Hz,fH=62.5Hz，此频段把工频50Hz及旁频带都包含进来，以便分析.为了搜取频谱在不同频率环境中的变化特征，随机调整a值，观察f1值与fH的变化情况，并计算△f值，当△f值的变化趋向平稳后，截取频率区段，因为此区段的平顶效果最好，频带的上升与下降，都会诱发信号的波动性变化.

5.2.2 小波变换

选择参数a、b，截取小波函数，并根据预先制定的电流频率区段，开始小波变换，定义公式为：

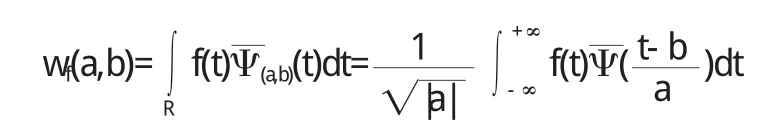
在实际操作中，这个计算公式已经被植入到计算机系统中，只要输入a、b参数值，就可在第一时间获取小波变换后的电流频率分量值.与信号处理相比，小波消噪在图像处理方面更具优势，一方面，噪音和图像的压缩方式不同，噪音与信号本身的性质特征是极其接近的，在故障检测、处理时，极容易被混淆；另一方面，图像电流频率分量光滑性好，即便是降噪之后，它与原信号之间也不会出现较大误差.

5.2.3 频移

本次研究选择的频移距离为37.5Hz，经细致检测发现，在37.5Hz-62.5Hz之内，频谱的变化几乎没有，此现象说明，频移变化并不会影响小波变换最终的频谱细化图，信号的原本性质是不会改变的.如此一来，检测人员便可放下心，在频移试验后，校验小波变换后，频谱细化信号的特征性质，进而判断故障源、故障问题、故障特征.

5.2.4 重采样

令m=4，表示频谱细化倍数为4倍，经统计计算可知，频谱分辨率为△f=0.25Hz.重采样的区间确定后，便可计算小波变换后频谱细化后的具体信号噪音，有利于做准确的消噪处理.

5.2.5 信号转换

信号转换虽说是最后一个步骤，但其确实计算故障分量的关键，就本次试验而言，故障分量为(1±3s)f1，该数值证明，小波变换中违背规律、特征的频谱会被精准的记录下来，故障分量越小，说明电动机的故障问题不大，故障分量越大，说明电动机转子断条、断裂处较多，故障问题严重.

从具体试验效果上看，通过小波变换对应的频谱细化信号，对模拟电动机各运行装置的运行状态有较大优势，一来，图像信号受环境干扰、影响不大，即便是在噪声很大的工厂中，信号也能有效、有序的传输到滤波器中，进行波形转换.二来，细化后的频谱信号，敏感度较高，即便细微的电力频率分量变化，也会影响故障分量值，被故障检测人员发现.但为了提高故障检测的准确性和及时性，小波变换提取的细化频段区间仍不断缩小距离，只有这样，对应的细化频谱才能真正模拟出电动机转子断条、断裂等细致信息，特别是在使用FFT计算方法之后，小波及小波变换的特性会愈加突出.

6 结论

通过上文对小波变换的频谱细化方案在电动机故障检测中的主要应用问题进行系统分析可知，图象经过小波变换后生成的小波图象的数据总量与原图象的数据量相等，即小波变换本身并不具有压缩功能.之所以将它用于电动机故障检测，是因为经过细化的频谱信号，在传播、自动化处理方面存在明显优势.简单通俗的说，就是把复杂的混乱的，乍一看没有什么规律，不好研究分析的函数，映射之类的分解成为微小的，规律性很好的，易于分析解决的小周期，小振幅的函数——小波.说简单了他就是数学上的一种化解，极限思想.只是延伸的很好，很强大.对我们实际生活的启发就是，当你碰到一个复杂的问题的时候，你可以尝试着把它化解成一些小的，易于理解的，然后再进行各个击破，最后再综合起来，最终解决问题.在未来几年，小波变换的频谱细化方案在工业故障诊断工作中的应用范围会越来越广泛，在智能化电子产品、高新科技发展速度迅猛的时代，小波变换的基础理论严谨、实用性价值高，对应的频谱细化方案是存在巨大科研价值与拓展空间的.

〔1〕蔡泽祥，俞亮，高爱云.大型电动机的内部故障诊断与保护方法[J].电力自动化设备，2002，22（107）:161-174.

〔2〕曹豫宁，李永丽，梅云，李斌.基于小波变换的频谱细化方法在电动机故障检测中的应用[J].继电器，2002，29（106）:111-113.

〔3〕徐巍，杨黎明.基于小波变换和独立分量分析的感应电动机故障检测和诊断研究[J].天津理工大学学报（社会科学版），2008，29（110）：14-23.

〔4〕姜万录，杨少辉，宋丽娜，姚志飞.频谱细化方法在干式真空泵故障诊断中的应用 [J].机床与液压，2008，28（09）:154-156.

〔5〕陈凯，许伯强，李和明，段翔颖.基于小波变换的改进LMS算法在异步电动机轴承故障诊断中应用[J].电力自动化设备，2008，11（109）:77-81.

〔6〕任震，张征平，黄雯莹，杨楚明.异步电动机早期故障检测技术发展评述 [J].华南理工大学学报 (自然科学版)，2001，28（111）:67-70.