将乐地区马尾松最优冠幅模型研究

张 鹏，王新杰，高志雄，许 昊，武文昊，王廷蓉，刘 乐

（北京林业大学 省部共建森林培育与保护教育部重点实验室，北京100083）

树木的地上部分主要由树干、树枝、树叶等部分组成，其中枝叶组成的树冠是高大乔木进行光合作用、呼吸作用等一系列活动的主要部分［1］。它决定树木的生活力和生产力，同时在树木生长过程中也是反映树木的长期竞争水平的重要指标［2］。在树冠结构中，冠幅（树冠直径crown width，CW）是树冠重要的特征因子［3］，在单木生长模型中经常用到冠幅和冠长率作为协变量预测树高或胸径生长量、生物量和树木枯损等［4-5］；此外，冠幅也是可视化的重要参数［6］。因此，研究冠幅的预测模型具有重要的意义。

国内外对冠幅的研究主要集中在定性和图表研究［7］，A.L.Duchaufour［8］首次确定了冠幅和胸径之间的关系，由于冠幅与胸径在实际当中比较容易被测定，很多研究者也通过温带、寒带、针叶用材林树种冠幅和胸径比值，来测定树种的断面积和林分株数密度［9-10］。吴志德［11］等采用线性回归研究了杉木胸径与冠幅的关系；梅光义［12］研究得出杉木人工林树冠直径与胸径在胸径范围为4～35cm时存在明显的线性关系。许多研究结果表明，林木胸径与冠幅的大小有密切关系，胸径越大，冠幅就越大［13］，有学者利用胸高直径、树高、胸高断面积、林分密度等因子建立了冠幅的线性关系［14-16］。雷相东［6］对长白落叶松等几种树种冠幅模型预测研究中，采用多元逐步回归模型进行冠幅的预测，结果表明，各树种的冠幅预测模型的修正后的决定系数R2在0.34～0.75之间，除了胸径与冠幅有较强的相关性外，被选入自变量的因子有林分密度（公顷株数或者用公顷断面积），以及竞争指标、枝下高和树冠比，拟合的模型可用于冠幅的预测。以往大多数研究只针对冠幅与胸径的线性关系，很少有对冠幅有关的方程进行系统的比较分析，通过其他树木变量和林分因子也被用来提高对冠幅的预测，如树高、冠长、树冠比、竞争因子、林分密度、立地因子等。以福建将乐马尾松纯林为例，建立马尾松林的冠幅预测模型，为其生长收获预测和经营决策提供依据。

1 研究地概况

研究区位于福建省三明市将乐国有林场，将乐县（117°05′-117°40′E，26°26′-27°04′N）位于福建省西北部，属于中亚热带季风区，具有海洋性和大陆性气候特点。境内地势复杂，以中、低山为主，森林资源丰富，全县山地面积19.2万hm2，其中有林地面积18.87万hm2，森林覆盖率达84.5%，林木蓄积量1 598万m3。将乐国有林场地处武夷山脉东南麓、金溪河畔，为低丘陵地带，海拔分布为400～800m，最高1 203m，最低140m。年平均气温18.7℃，年平均降雨量1 669mm，年平均蒸发量1 204mm，无霜日287d，气候温和，土层深厚，土壤肥沃，以红壤为主，并分布有黄红壤，适宜培育以杉木、马尾松为主的用材林和乡土珍贵树种。

2 材料与方法

2.1 资料收集与整理

2010、2011、2012年在福建将乐国有林场进行实验数据采集。按年龄分布共设置马尾松人工林固定、临时标准地14块（图1）。标准地的统计信息见表1。根据地势设置标准地大小，面积为400～600 m2。在进行标准地调查时，实测相关林分结构特征指标，主要包括林分起源，林分年龄，胸径，树高，郁闭度，枝下高以及东、南、西、北4个方向的冠幅长度，其中树高以精度较高的激光测高器进行测量，冠幅是以皮尺对树冠最宽幅的垂直投影的水平距离的测量。共调查马尾松980株，所调查的样地中，随机选取11块样地（707株）作为建模数据，剩下的3块（273株）作为检验数据，统计信息见表1。

表1 建模数据和检验数据统计信息Table 1 Summary statistics for modeling and validation datum sets

图1 马尾松样地分布Fig.1 Map of P.massonianaplot data

该研究中冠幅为东、南、西和北4个方向的平均值，计算公式为：

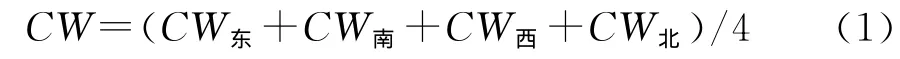
式中，CW东、CW西、CW南和CW北分别代表东、西、南、北冠幅长度［6］。

2.2 基础模型

选用11种常用的冠幅-胸径模型（表2），利用残差平方和（RSS）、剩余均方根误差（RMSE）和调整后的决定系数（adj-R2）3个指标对模型进行评价，选择精度最高的作为基础模型。其中，RSS和RMSE的值越接近0而adj-R2的值越接近1，说明模型的精度越高［15，17］（表2）。

表2 冠幅基础模型Table 2 Crown diameter basic model

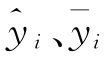
2.3 林分变量

除与胸径相关外，冠幅还受其他林分变量的影响，如树木大小和林分活力因子、立地条件因子以及林分竞争因子等［6］。同时在模型中增加一些林分变量能降低林分或单木差异对冠幅的影响［17］。本研究考虑的林分变量有：

树木大小和林分活力因子—林分年龄（A）、林分密度（M）、树高（H）、冠长（CL）［16，18］；

林分竞争因子—样地算术平均直径（MD）、样地优势木平均高（Ht）、样地优势木平均直径（Dt）、样地算术平均树高（MH）［18］。

2.4 模型求解和检验

本研究模型的计算是基于冠幅和胸径的实测数据，利用R软件［14］的nls模块实现的，得出各模型的参数。

模型评价主要考虑模型的拟合统计量，在选出的基础模型中，添加与冠幅相关性较高的林分变量，利用偏差（Bias）、剩余均方根误差（RMSE）和调整后的决定系数（adj-R2）3个指标对模型的预估能力进行评价，经过综合分析，选出拟合精度最高的作为最优模型。

3 结果与分析

3.1 模型选择

表3为模型1～模型11的评价指标，其中模型10和模型11为3参数模型，其他模型都为2参数模型。RSS和RMSE的值越接近0，adj-R2的值越接近1，则说明模型的拟合能力越强。综合分析，从表3中可以看出，在建模数据中，2参数最好的模型为模型3，3参数最好模型为模型11。

对模型3和模型11做方差分析，结果表明，两模型间差异显著（F=47.79，p＜0.000 1），且模型11表现较好，因此，选择模型11为建立马尾松冠幅-胸径关系的基础模型，其结构形式为：

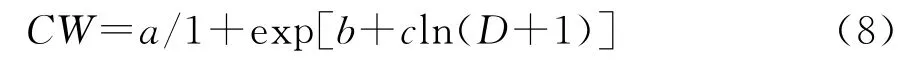
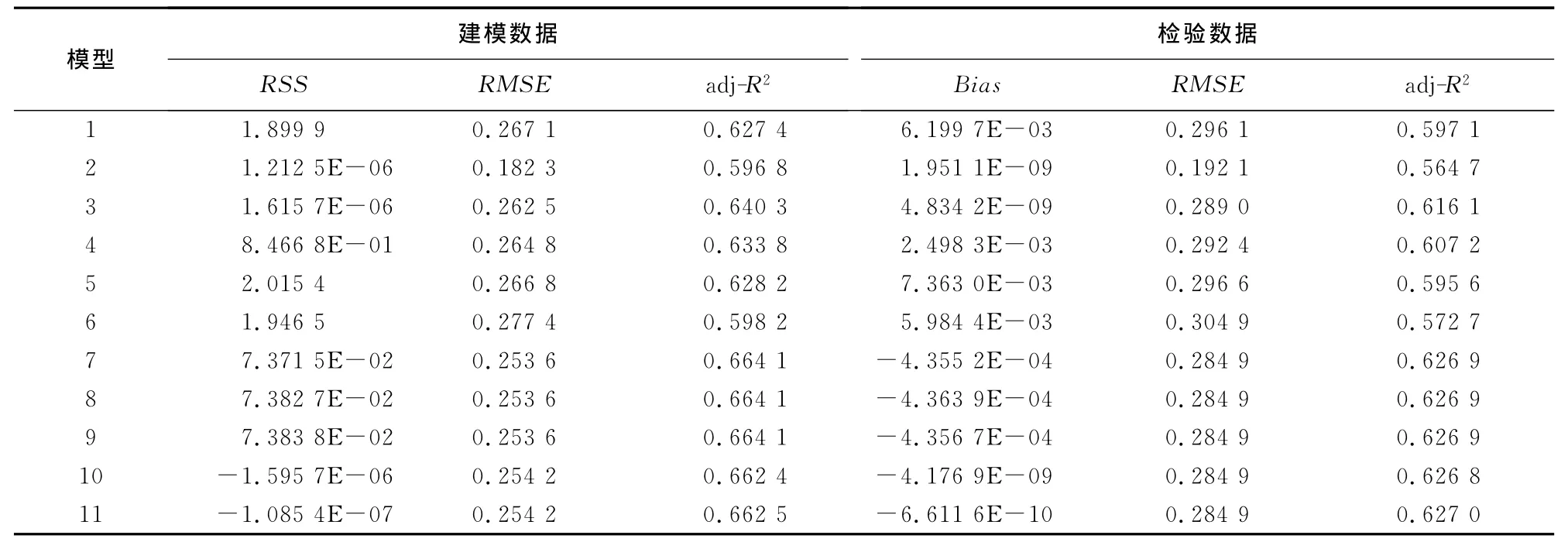
表3 各模型评价指标Table 3 Model evaluation indexes

3.2 模型改进

为了降低林分或单木水平随机效应差异对冠幅的影响，在模型中增加了与冠幅相关性较大的林分优势木平均高（DH）、对象木冠长（CL）和每公顷株数（M）作为新增加的林分变量，模型表达式为：

式中：CW为对象木冠幅，Ht为样地优势木平均高，M 为每公顷株数，CL 为对象木冠长，a，b，c，a1，b1，c1为参数。模型中各参数值见表4。

对式（8）和式（9）做方差分析，结果表明，两模型差异显著（F=47.56，p＜0.001），因此，式（9）能够更好地预测马尾松的冠幅大小。

表4 模型中参数值Table 4 Parameters for each model

3.3 模型评价

运用验证数据对式（9）进行验证，利用偏差、均方根误差和调整后的决定系数3个指标比较2模型间的精度。验证结果见表5。从表5中可以看出，在考虑了样地优势木平均高、每公顷株数和冠长等林分变量之后，偏差、均方根误差减小，调整后的决定系数明显增大，说明改进后的模型能够更好地模拟当地马尾松的冠幅与胸径的关系。

表5 模型评价指标Table 5 Model evaluation indexes

4 结论

树冠在树木的生长过程中具有重要的作用，它反映了树木的长期竞争水平，因此，冠幅预测对于林木生长等都有重要的意义。本研究建立了马尾松冠幅预测模型，发现对冠幅有显著影响的因子包括林木胸径、林分密度、冠长以及林分优势木平均高，这与雷 相 东［6］、D.C.Brabg［19］等 人 的 研 究 基 本 上 一致，林分密度与冠幅呈负相关，即随着林分密度的增加，林木会逐渐限制其树冠的发展或逐渐趋于死亡；冠长大小可以表征林木进行光合作用能力的强弱，冠长越长，表明树冠所接受到的太阳光越多，越有利于冠幅的增大。胸径、林分优势木高、林分密度、冠长对针叶树种马尾松的冠幅有显著影响。

关于冠幅与胸径的相关的研究较多，但尚未见对福建地区针叶树种马尾松的研究。本文使用福建省将乐国有林场马尾松调查数据，选用11种冠幅模型，用调整决定系数adj-R2、残差平方和RSS、剩余均方根误差RMSE对模型进行比较，选出基础模型，对选出的基础模型11通过添加林分变量进行改进，运用检验指标进行检验分析，改进模型Bias=-8.777 4E-10、RMSE=0.243 8、adj-R2=0.726 9，偏差、均方根误差减小，调整后的决定系数明显增大，改进模型精度明显提高，能够更好地模拟当地马尾松的冠幅与胸径的关系。本研究所选出的最优冠幅模型适用于福建将乐地区马尾松。

［1］ 刘兆刚，舒扬，李凤日.樟子松人工林一级枝条基径和枝长模型的研究［J］.植物研究，2008，28（3）：244-248.LIU Z G，SHU Y，LI F R.Modeling for primary branch length and branch diameter of Mongolian scots Pine Trees［J］.Bulleyin of Botanical Research，2008，28（3）：244-248.（in Chinese）

［2］ BIGING G S，DOBBERTINM.A comparison of distance-dependent competition measures for height and basal area growth of individual conifer trees［J］.For.Sci.，1992，38（3）：695-7201.

［3］ KALLIOVIRTA J，TOKOLA T.Functions for estimating stem diameter and tree age using tree height，crown width and existing stand database information［J］.Silva Fennica，2005，39（2）：227-248.

［4］ MONSERUD R A，STERBA H.A basal area increment model for individual trees growing in even-and uneven-aged forest stands in Austria［J］.Forest Ecology and Management，1996，80（1／3）：57-80.

［5］ RUSSELL M B，WEISKITTEL A R.Maximum and largest crown width equations for 15tree species in Maine［J］.Northern Journal of Applied Forestry，2011，28（2）：84-91.

［6］ 雷相东，张则路，陈晓光.长白落叶松等几个树种冠幅预测模型的研究［J］.北京林业大学学报，2006，28（6）：75-79.LEI X D，ZHANG Z L，CHEN X G.Crown-width prediction models for several treespecies including Larix olgensisin Northeastern China［J］.Journal of Beijing Forestry University［J］.2006，28（6）：75-79.（in Chinese）

［7］ WYKOFF W R.A basal area increment model for individual conifers in the Northern Rocky Mountains［J］.Forest Science，1990，36（4）：1077-1104.

［8］ DUCHAUFOUR A L.ame.Management dela forest de coompiegne［J］.Revue Eauxet Forest，1903，42：65-78.

［9］ BRIEGLEB P A.An approach to density measurement in douglas fir［J］.J.Foresty，1952，50：529-536.

［10］ HEMERY G E，SAVILL P S，PRYOR S N.Application of the crown diameter-stem diameter relaitionship for different species of broad leaved trees［J］.Forest Ecology and Management，2005，215（1／3）：285-294.

［11］ 吴志德，骆期邦.林分标准密度（立木株数）确定方法的研究［R］.长沙：中南林业调查规划，1989：26-28.

［12］ 梅光义，孙玉军.杉木风景游憩林冠径与胸径关系研究［J］.植物研究，2013，33（4）：416-420.

［13］ BRABG D C.A local basal area adjustment for crown width prediction［J］.Northern Journal of Applied Forestry，2001，18（1）：22-28.

［14］ BECHTOLD W A.Largest-crown-width prediction models for 53species in the Western United States［J］.Western Journal of Applied Forestry，2004，19（4）：245-251.

［15］ BECHTOLD W A.Crown-diameter prediction models for 87 species of stand-grown trees in the Eastern United States［J］.Southern Journal of Applied Forestry，2003，27（4）：269-278.

［16］ IHAKA R，GENTLEMAN R.R：a language and environment for statistical computing ［DB／CD］.Vienna，Austria：R Foundation for Statistical Computing，2004.

［17］ PINHERIO J C，BATES D M.Model building for nonlinear mixed effects model［R］.Deparment of Statistics，University of Wisconsin，Madison，Wis.1998.

［18］ CALAMA R，MONTERO G.Interregional nonlinear heightdiameter model with random coefficients for stone pine in Spain［J］.Canadian Journal of Forest Research，2004，34（1）：150-163.

［19］ BRABG D C.A local basal area adjustment for crown width prediction［J］.Northern Journal of Applied Forestry，2001，18（1）：22-28.