企业信用风险评价模型估计的有偏性检验

孙焱林，叶俊显，吴裕晴

（华中科技大学 经济学院，武汉 430074）

1 问题的提出

信用风险作为银行业务风险的一个重要组成部分，对银行开展信贷业务产生重要的影响，因此，国内外学者一直都非常关注信用风险并对其做了大量研究。这些研究主要集中于信用风险的评价模型，从最初的5c法、信用风险评分模型、多元判别分析，到非线性判别分析、Logistic模型、BP神经网络模型，再到现代的KMV公司的EDF模型、麦肯锡的CPV模型、J·P摩根的Credit Metrics TM模型、CSFB的Credit Risk+模型等。由于回归类模型的简单和有效性，在评价企业信用风险的理论研究和实践应用当中，很多学者和银行都采用回归类模型预测企业的信用风险，包括以Z-Score模型为代表的多元判别分析模型、非线性判别分析模型和Logistic模型。回归模型开始把企业的各项指标值同违约概率联系起来，通过运用历史数据进行回归寻找企业各指标值同违约概率之间的准确关系，作为对企业未来信用风险进行预测的方法。

由于许多理论研究和银行实践在采用回归模型设计企业信用风险评价模型时，模型估计所用数据均来自银行历史客户资料库中的企业数据，而这些客户企业的数据都已通过了银行现有评价系统的筛选，是非随机数据或受约束数据，以这些数据所建立的回归模型其实是一个受约束的回归。然而，在应用评价模型时，不仅会涉及对银行的历史客户企业进行评价，还会涉及对银行的非客户企业进行评价，但这些企业的数据并非全部都能满足约束，因此，对全部企业都适用的信用风险评价模型应该是以无约束的数据进行回归所建立的模型，即以包括银行的历史客户企业和非客户企业的数据进行回归所得到的模型。既然合理的信用风险评价模型应当以无约束数据回归为基础建立，那么现有的研究和实际用受约束数据回归建立信用风险评价模型，就默认了受约束数据回归和无约束数据回归是一致的。但受约束数据回归的结果与无约束数据回归的结果并非必然一致，如果二者出现了差异，就会导致信用风险评价模型的有偏估计，从而导致对违约概率的估计出现偏误，最终导致贷款决策的失误。

从回归类信用风险评价模型估计有偏性产生的原因分析，可以看出有偏性是否出现关键在于数据约束是否会对回归模型的结果产生影响。因此从比较无约束数据的回归结果和受约束数据的回归结果是否一致入手分析，如果两者不一致，就可以说明用银行历史客户企业数据进行的回归对信用风险评价模型的估计是有偏的。

2 无约束数据和受约束数据的设计

2.1 Logistic模型和银行现有评价系统的假设

(1)银行现有评价系统的假设说明。

第一，银行现有评价系统不进行等级划分，只设定一个评价标准，如果申请企业的指标达到评价标准，银行就同意向其提供贷款，否则，就拒绝提供贷款；第二，所有企业的性质及风险特点相似，因而可以采用同一评价系统进行评价；第三，对定性指标只作简单说明，不涉及具体的评价参考值，直接模拟定性指标的得分，而定量指标则模拟出其数据；第四，各项指标的取值都服从均匀分布。

(2)Logistic模型的运用说明。

Logistic回归模型是对二分因变量进行回归分析时最普遍使用的一种多元统计方法。它采用Logistic回归函数，利用样本数据估计出各个参数的数值，再经过一定的推导运算，得出事件发生的概率。在用Logistic回归模型来评价企业信用风险的过程中，要判断一笔企业贷款是否违约，只有“是”和“否”两个状态，因此，因变量只取两个值，表示一种结果的两种可能性。把Y=1定义为贷款违约，Y=0定义为贷款没有违约。即：

表1 Logistic模型评价指标及系数假设

其中，pi代表的是通过模型计算出的申请企业的违约概率，Yi值反映了申请企业信用状况的数量特征，Xi（i=1，2，…，n）为自变量，反映申请企业信用状况的指标变量。当计算出来的申请企业的违约概率超过银行设定的标准值时，为了降低贷款风险，就拒绝向该企业提供贷款。

Logistic模型本身能够保证所得的违约概率落在0～1之间，从而避免了其他回归模型会导致的计算结果超出合理边界的问题；Logistic模型避免了对企业各项指标与违约概率之间线性相关的假定，即运用非线性的方法来研究指标值与违约概率之间的回归关系；回归不先假定任何概率分布，这与一般多元判别方法正态分布假设的局限不同，在变量不满足正态分布情况下，其判别正确率一般要高于其他判别分析法的结果；Logistic模型可以对每个变量进行显著性检验。由于这些特点，Logistic回归模型从20世纪70年代以来在信用风险评价的理论研究和实践中都得到了广泛应用。

(3)Logistic模型评价系统的假设。

假设Logistic模型评价系统用财务、经营管理素质、发展前景、资信状况等四项一级指标下的13项二级指标建立信用风险评价模型，评价指标及系数假设如表1所示。

(4)银行现有评价系统假设。

将银行现有评价系统（以下简称为S模型）假设为单一条件模型：资产负债率（ALR）≤15%，即在银行现有评价系统中，如果申请企业的资产负债率小于等于15%，银行就同意向其提供贷款；否则，就拒绝提供贷款。

(5)指标取值的分布区间假设。

财务指标的各项二级指标模拟其实际数值，经营管理者素质、发展前景和资信状况等各项二级指标直接模拟其得分，各指标取值的分布区间假设如表2所示。

2.2 蒙特卡罗方法模拟数据

(1)模拟生成无约束的A组企业的数据。

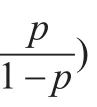
(2)按照S模型假设从A组中筛选受约束的B组企业的数据。

根据S模型的评价标准——资产负债率（ALR）≤15%，对A组的300个企业进行筛选，最终满足筛选条件的企业共有43个，定义为B组企业。

3 有偏性检验

3.1 样本数据的回归分析

(1)无约束数据的回归。

表2 指标取值的分布区间假设

表3 无约束数据的回归结果

从回归的结果可以看出，回归的拟合度在85%以上，所有变量系数的P值都无限小，说明在1%的水平上，所有变量系数都是显著的。

(2)受约束数据的回归。

从回归的结果可以看出，虽然回归的拟合度在90%以上（可能的原因之一是B组只有43个观测值，而A组有300个观测值），且受约束变量ALR的系数在5%的水平是显著的，但其系数3.9951远远超过无约束数据回归下变量ALR的系数0.5500。同时，ART、MI、EB、PS、SAC这五个变量的系数在5%的水平上都是不显著的。

(3)受约束数据回归系数的Wald检验。

以无约束数据回归中各变量的系数为参照，对受约束数据回归系数进行Wald检验，结果如表5所示。

表5 受约束数据回归系数的Wald检验

从Wald检验的结果当中可以看出，在5%的显著水平下，包括截距在内的14个系数中，受约束变量ALR和未受约束变量MA的系数均显著不等于无约束数据回归中对应变量的系数，从而可以认为无约束数据回归与受约束数据回归的结果并不一致。

3.2 预测结果分析

表6 两模型下违约概率的预测结果

按照与A组企业相同的条件模拟100个新企业13项指标的取值，将该组企业定义为C组企业，分别用无约束数据回归模型和受约束数据回归模型预测这100个企业的违约概率，然后对这两组预测值进行对比分析。

(1)预测违约概率。

分别用无约束数据回归的结果和受约束数据回归的结果，预测C组100个企业的违约概率，结果如表6所示。

(2)两模型预测结果的特征值比较。

根据无约束数据回归模型和受约束数据回归模型预测的C组100个企业的违约概率，分别计算两模型下C组全部企业（100个）、满足S模型评价标准的企业（15个）、不满足S模型评价标准的企业（85个）这三组企业的均值和方差，并进行相等性检验，检验的结果如表7所示。

表7 两模型预测结果的特征值比较

从无约束数据回归模型和受约束数据回归模型预测结果的均值、方差的比较可以看出：对于满足约束条件的企业组，两类模型预测结果的均值、方差都比较接近，相等性检验也是不显著的；但对于不满足约束条件的企业组，两类模型预测结果的均值、方差在统计上都是显著不相等的，受约束模型计算的均值比无约束模型计算的均值高约29%，差异较大，从而导致全部企业在两类模型下的预测结果也出现较大差异。

4 结论

回归分析和预测分析的结果表明，在银行信用风险评价当中，无约束数据回归模型和受约束数据回归模型并非必然一致，基于银行历史客户资料库中的企业数据进行回归得到的信用风险评价模型的估计是有偏的。因此，在理论研究和实践当中，应该把这种有偏性考虑进回归方法所建立的信用风险评价模型当中，比如可以对未提供贷款的申请企业进行后续追踪，利用其在申请贷款后一年或两年内经营失败作为其违约的替代变量，这样就可以把银行的非客户企业数据纳入到回归模型当中，将模型由受约束数据回归变成无约束数据回归，以达到减弱有偏性影响的效果，从而更加准确地预测企业的信用风险。

[1]Altman E.Financial Ratios,Discriminant Analysis and The Prediction of Corporate Bankruptcy,”[J].Journal of Banking and Finance,1968,23(4).

[2]Altman E R,Haldeman P.Narayanan,Zeta Analysis:A New Model To Identify Bankruptcy Risk of Corporation[J].Journal of Banking and Finance,1977,1(1).

[3]Ohlson J,Financial Ratios and The Probabilistic Prediction of Bankruptcy[J].Journal of Accounting Research,1980,18(1).

[4]胡胜,朱新蓉.我国上市公司信用风险评估研究——基于Logit模型的分析[J].中南财经政法大学报,2011,(3).

[5]李萌.Logit模型在商业银行信用风险评估中的应用研究[J].管理科学,2005,(2).

[6]糜仲春,申义,张学农.我国商业银行中小企业信贷风险评估体系的构建[J].金融论坛,2007,(3).