《电路分析基础》教学中一阶电路分析方法的探索

王德波

（南京邮电大学电子科学与工程学院，江苏 南京210003）

0 引言

电路分析基础是电子类专业的技术基础课程，其教学任务是通过本课程的学习使学生掌握电路的基本概念、基本理论和电路分析的基本方法，为后续课程的学习提供必要的理论基础知识。由于该课程与后续专业课程如“模拟电子技术”“数字电子技术”等课程密切相关，具有基础课和专业课之间的桥梁作用，因此其教学有着十分重要的地位。

而一阶电路分析对于该课程的学习具有承前启后的作用，它是该课程由静态电路向动态电路学习的过渡。静态电路（电阻电路）的激励与响应的VCR关系为代数方程，响应仅由激励引起；动态电路（电容或电感电路）的激励与响应的VCR关系为微分方程，响应与激励的全部历史有关。因此，一阶电路分析方法的学习对于该课程的学习具有至关重要的地位。

1 一阶电路分析方法

通常，基本的一阶电路有两种：RC串联电路（图1）和GL并联电路（图2）。无论是求零输入响应、零状态响应还是全响应，总是以电容电压或是电感电流为主要分析对象建立其微分方程 （式1和式2）求解。

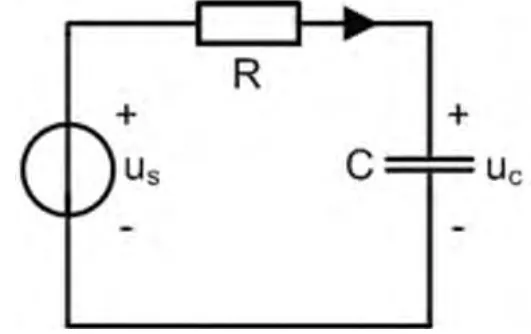
图1 RC串联电路

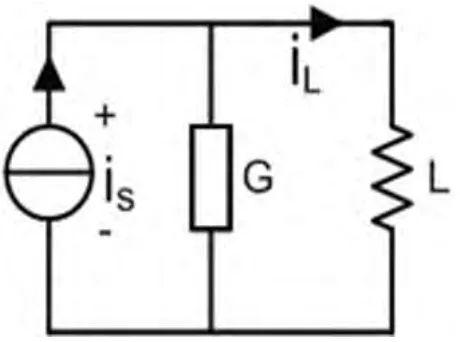
图2 GL 并联电路

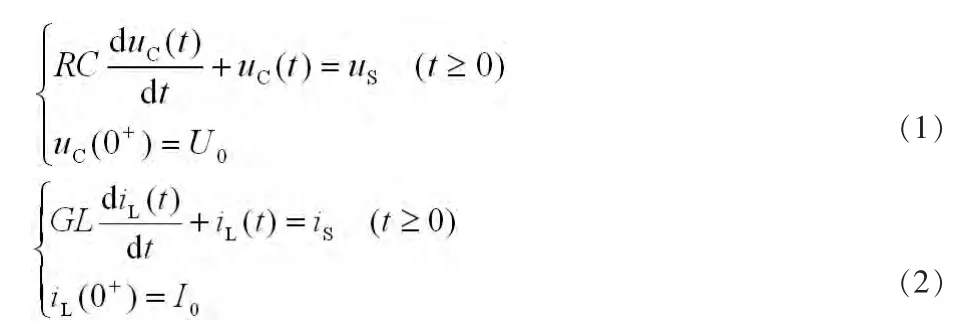
但实际上一阶电路千差万别，响应也各不相同。仅计算电容电压或是电感电流显然是不够的，而且是繁琐的。因此寻求一种能直接计算一阶电路任意响应的简便方法是十分有必要的，而三要素法正适合于求解恒定激励下一阶电路的响应。在恒定激励下，采用三要素法得到响应的一般表达式为：

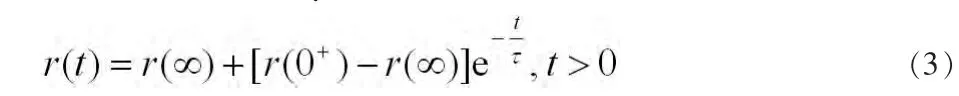
其中，r(∞)为稳定值，r(0+)为初始值，为时间常数。

三要素法求直流激励下响应的一般步骤：

1）初始值r(0+)的计算（换路前电路已稳定）

（1）画t=0-图，求初始状态：电容电压uC(0-)或电感电流 iL(0-)。

（2）由换路定则，确定电容电压或电感电流初始值，即uC(0+)=uC(0-)和 iL(0+)=iL(0-)。

（3）画0+图，求其它初始值——用数值为uC(0+)的电压源替代电容或用iL(0+)的电流源替代电感，得电阻电路再计算。

2）稳态值 r(∞)的计算(画稳定图)

根据t＞0电路达到新的稳态，将电容用开路或电感用短路代替，得一个直流电阻电路，再从稳态图求稳态值r(∞)。

3）时间常数τ的计算(开关已动作)

根据输出电阻的等效电路图，先计算与电容或电感连接的电阻单口网络的输出电阻Ro，然后用公式τ=RoC或τ=L/Ro计算出时间常数。

4）将 r（∞），r（0+）和代入三要素公式得到响应的一般表达式。

基于以上的分析，不难得出结论，由三要素法求解一阶电路响应需要画4张等效电路图。其中画t=0-图与画稳定图类似，画0+图和画输出电阻的等效电路图是重点和难点。

2 对本科教学的意义

在《电路分析基础》教学中，如果教师能够使学生对一阶电路的分析方法理解深刻，并能熟练的画出四张等效电路图。学生就可以既能回顾静态电路的基础知识，又可以加深对动态电路的理解。对后面的正弦稳态电路和耦合电路的学习具有积极有效的意义。

［1］沈元隆，刘陈.电路分析基础[M].3 版．北京：人民邮电出版社，2008．

［2］成谢锋，周井泉.电路与模拟电子技术基础[M].北京：科学出版社，2012．