焦炭冷态强度多元线性回归分析预测模型的研究及应用

吴玉森，刘 辉，张代林，郑明东

（1．安徽工业大学计算机科学与技术学院，安徽 马鞍山243002；2．安徽工业大学化学与化工学院，安徽 马鞍山243002）

一般入炉煤挥发分V和粘结指数G对焦炭质量有着显著影响，主要表现在V能间接地反映焦炭气孔率的高低，其值越高越有助于焦炭充分燃烧；G主要能够反映出氧化对煤粘结性的影响［4］，是煤形成焦炭的前提和必要条件。而胶质层最大厚度Y的大小同粘结指数G对炼焦的影响是一样的，并且V、G和Y在配煤下均有较好的加和性。其中焦炭冷态强度是指焦炭抗碎强度M40和焦炭耐磨强度M10。

笔者选用入炉煤的挥发分V、粘结性指数G和胶质层最大厚度Y作为影响因素，在MATLAB下进行多元线性回归分析，拟合出焦炭冷态强度预测模型，再进行F检验和t检验，以建立简单、准确的预测模型。配煤专家可以根据预测模型快速估算出焦炭冷态强度性能，立刻能掌握焦炭合格情况，从而可以有效地预测出满足要求的焦炭，为稳定焦炭生产和提高焦炭质量提供理论依据［5］。

1 模型建立及分析

1．1 基于最小二乘法的多元线性回归模型

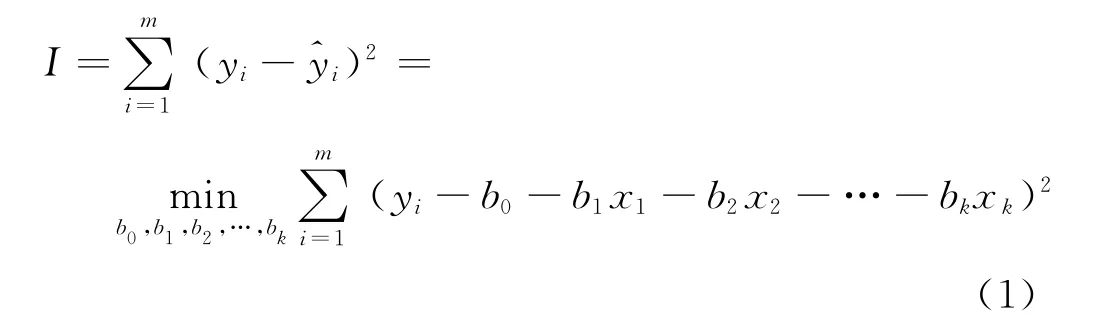
式（1）中，I为b0、b1、b2、…、bk的k＋1元非负二次函数，故其最小值总是存在的。根据多元函数求极值的必要条件，将求I对bi的偏导数并令其为0（1≤i≤k），得到正规方程［6］（P39-40）：

1．2 模型检验

1．2．1 回归模型的显著性检验

1．2．2 自变量的显著性检验

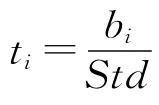
2 实验分析及结果

2．1 焦炭冷态强度预测模型的建立

本文所选用的数据来自于某焦化厂的生产数据，同时对数据进行筛选，剔除异常数据，所列数据如表1所示。

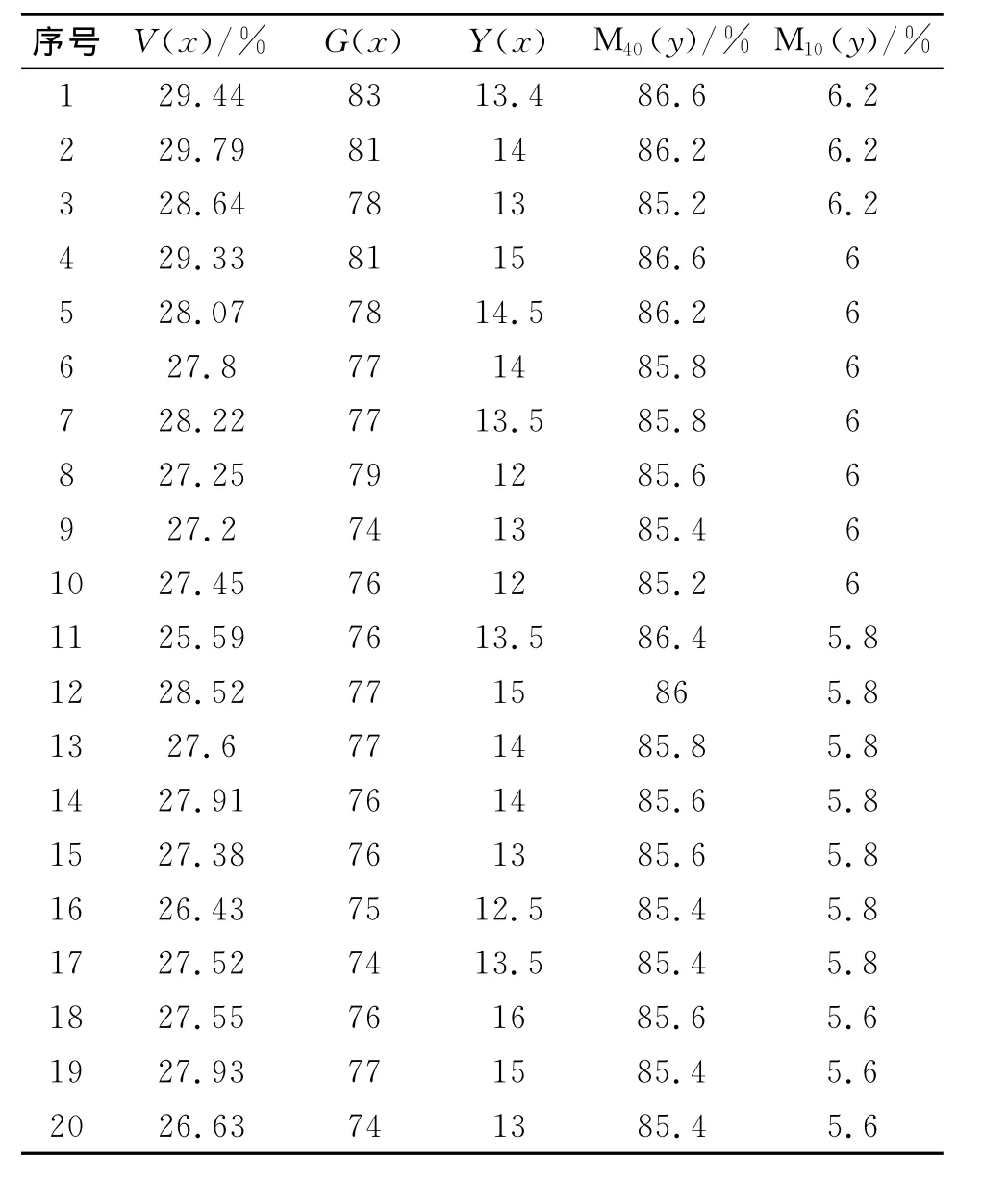
表1 入炉煤生产数据及焦炭冷态强度指标

在MATLAB下，对表1中入炉煤的挥发分V、粘结性指数G、胶质层最大厚度Y为自变量，M40、M10为因变量，分别进行三元线性回归拟合，得出M40和M10的预测模型：

因此，通过式（3）、（4）较好地建立了焦炭冷态强度的预测模型。

2．2 焦炭冷态强度预测模型的显著性检验

对式（3）、（4）进行F检验，将计算出的方差分析如表2所示。

由表2中的数据分析可知，在给定显著性水平α＝0．05，查得F分布临界值表F0．95（3，16）＝3．239。由此可判断本文中求得的焦炭冷态强度M40、M10与入炉煤V、G、Y的线性关系在95%的水平下显著成立。

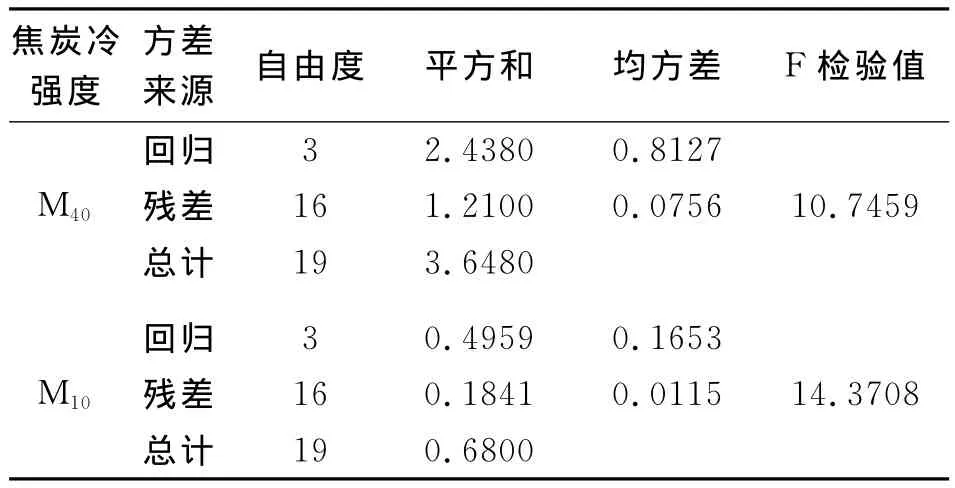
表2 预测模型方差分析表

再对xV、xG、xY进行t检验，其回归系数的估计值、标准误差和t检验值如表3所示。

表3 t检验相关结果

由表3中的数据分析可知，在给定显著性水平α＝0．2，查得t分布临界值表t0．1（16）＝1．3368。由此可说明M40与M10的3个参数bi均与0有显著差异，相对应的自变量xi均对因变量y的“贡献”显著，即认为入炉煤的V、G、Y对 M40与 M10的影响是显著的。

因此，入炉煤的V、G、Y与焦炭冷态强度 M40、M10具有较高的相关性。

2．3 焦炭冷态强度预测模型的实际检验

某焦化厂对焦炭冷态强度的要求为：M40的预测值不能低于82%，与实际值的绝对误差最大不能超过2%；M10的预测值不能高于6．5%，与实际值的绝对误差最大不能高于0．3%。在图2的实际曲线与预测曲线对比中，M40的预测范围在85．04%～86．49%，平均预测值为85．73%，相应的绝对误差在0%～0．66%，平均误差为0．286%；M10的预测范围在5．67%～6．07%，平均预测值为5．875%，相应的绝对误差在0．01%～0．21%，平均误差为0．094%。因此，M40、M10的预测值与实际值的误差均在可接受范围内，较准确地预测出焦炭冷态强度，且预测模型能较好地反映出其实际生产趋势和波动情况，故预测模型可投用于实际生产。

图1 焦炭冷态强度M40和M10的实际曲线和预测曲线对比图

3 预测模型在配煤系统的应用

最优配比的寻求，是根据达丰焦化厂历史配比数据和进厂煤信息，动态地选取单种煤和设定配比区间来进行的，故设计出“最优配比”算法，其主要步骤如下：

Step 1 根据某焦化厂历史配比数据与进厂煤信息，获取 N 个单种煤Q＝（Q1，Q2，…，QN）。

Step 2 参考配煤专家给定的配比经验值，并将单种煤Qi的上下界设置成非负区间［ai，bi］，且必须满足0≤ai≤bi≤100。若bi-ai的长度较大，则该算法时间复杂度较大。N维配比向量P＝（pQ1，pQ2，…，pQN），其中，pQi为单种煤Qi的配比，ai≤pQi≤bi，1≤i≤N。

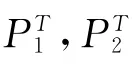
Step 4 如果M不为空，则依次从M 中取出解向量Pr，并计算该解向量所对应案成本cr，将最低的配煤方案成本cr所对应的解向量称为最优配比的寻求。如果M为空：根据配煤专家的建议，要么修改M40、M10的约束条件，重复Step 3～Step 4，直到 M不为空为止；要么返回step 1，重新选煤。

因此，该最优配比算法流程如图2所示。

4 结语

1）采用配合煤的V、G、Y为自变量，对焦炭冷态强度进行多元线性回归，建立其预测模型。

2）通过F检验和t检验，验证了基于最小二乘法的可行性；通过实际检验，说明模型预测能力较准确，能较好地反映实际情况。

3）设计了寻求最优配比应用方法，求得配煤的最优配比。在煤源供应不变下，可用该配比连续生产，以稳定焦炭质量。

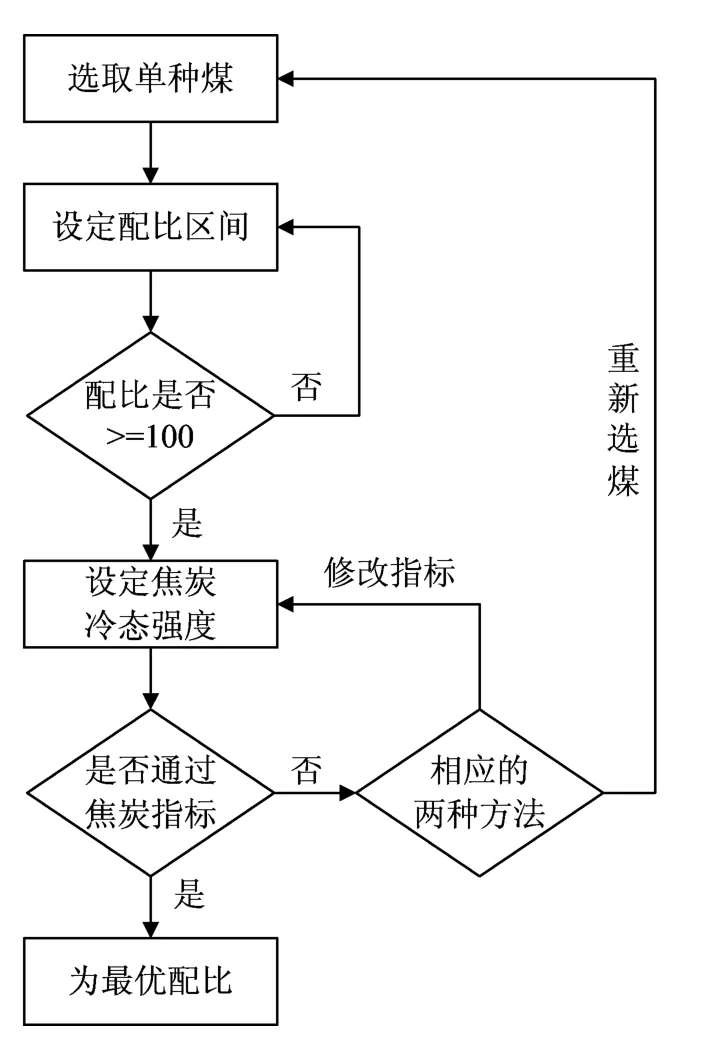
图2 最优配比算法流程图

［1］姚昭章，郑明东．炼焦学［M］．北京：冶金工业出版社，2005．

［2］姜静，宫春晖．神经网络在焦炭质量预测模型中的应用［J］．沈阳理工大学学报，2013，32（2）：26-27．

［3］杨扬，杨逸．40kg试验焦炉在预测焦炭质量中的应用［J］．科技情报开发与经济，2009，19（11）：202-203．

［4］胡德生．宝钢焦炭强度预测和配煤煤质控制［J］．宝钢技术，2000（3）：30-34．

［5］邓志平，张代林．优化配煤及焦炭质量的研究探讨［J］．江西冶金，2014，34（4）：3-3，8．

［6］马立平．回归分析［M］．北京：机械工业出版社，2014．

［7］王岩，隋思涟，王爱青．数理统计与MATLAB工程数据分析［M］．北京：清华大学出版社，2006．

［8］杨秀华，丁玉献．运用回归分析对炼焦生产的预测与控制［J］．煤质技术，2004（6）：25-26．

［9］孙荣恒．应用数理统计（第3版）［M］．北京：科学出版社，2013．