基于Petri网行为轮廓寻找业务流程变化域方法

郭圆圆，赵前进，刘祥伟

（安徽理工大学，安徽 淮南232001）

随着网络的普及和发展，各种业务系统不断涌现，人们对业务流程建模的理论和技术方面也提出了更多的要求，设计者为满足这种特殊要求的流程模型，将实际要求转换为业务流程是系统软件在应用环境中的重要任务之一。由于理论模型的简单和单一，在实际中不能很好地进行分析，转化出具有一致性、准确的和符合实际的模型已变得十分迫切。企业根据需求由源模型设计出的目标模型，再根据目标模型与源模型的一致性来判断目标模型是否符合，重要的是找出目标模型的变化部分，进而找出变化域，再用目标模型和源模型的对应关系，对源模型进行改造，这就是提高和完善模型的一个关键性问题。

目前有许多学者在研究变化区域时基本上是从序列角度和流程模型的一致性进行考虑，Matthias等在研究变化域传播时，利用行为等价的严格序概念对活动变迁的一致性进行检测，Matthias在文献［3］中根据行为轮廓的相关概念，去定义一些行为关系的活动变迁对进行匹配，然后通过给定节点，寻找对应的变迁区域，根据文献［1］和［4］可以知道，这些方法虽然都能找到变化域，不过都存在自身的局限性和不完整性。受郝文君的基于petri网的业务流程寻找最小变化域的方法影响，这篇文章给出的是寻找最小变化域的方法。而我们是找变化域，给出源模型，再用一致性关系给出源模型所对应的目标模型，分析源模型和目标模型之间的一致性匹配关系，找出模型的变化域。本文是给出关于寻找一般变化域的方法，以前很少说明，前面给出了寻找变化域的重要性，怎么找呢？本文通过变化节点寻找变化域的方法。

在本文中，笔者建立一个流程模型，并给出一些相关的概念，给出寻找变化域的方法结合实例给出源模型，对源模型进行分析中，提出一种通过流程网的动态行为特征、行为约束以及模型的一致性分析给出目标模型，再对目标模型进行分析，首先确定变化域的范围，并在此基础上找出变化域。

1 基本概念

这部分主要介绍本文中所用到的一些基本概念，其次是对模型图进行分析。

定义1（petri网） 满足下列条件的三元组N＝（S，T，F）称为一个petri网：

1）S是有限库所集，T是有限变迁集。

2）S≠φ，T≠φ且S∩T＝φ。

3）F＝（S×T）∪（T×S）表示流关系。

在文献［2］和［6］中，有关petri网中的前集和后集、标识、可达性和变迁序列，以及网的子集等相关概念在这就不再一一给出了。

Petri网存在一条从始点到终点活动的路径，以保证网是活的、可达的，不出现死锁。这就用到了弱序关系，众所周知，弱序关系是所有关系的基础，因此，在介绍行为轮廓之前先介绍弱序关系。

定义2［6］（弱序关系） （N，［i］）是一个工作流系统，弱序关系≻⊆T×T包括所有活动变迁对（x，y），若存在j∈｛1，…，n-1｝，并且j＜k≤n，这样存在一个发生序列σ＝t1，…，tn，使（N，［i］）［σ〉有tj＝x，tk＝y，则x，y是弱序关系，记作x≻y。

根据petri网中不同的2个活动变迁以及它们之间的流关系，先给出严格序、排他序和交叉序。

定义3［6］（严格序） （N，［i］）是一个工作流系统，严格序关系→⊆T×T对所有的活动变迁对（x，y）有x≻y但y≻x，则称x，y是严格序关系，记作x→y。

定义4［6］（排他序） （N，［i］）是一个工作流系统，排他序关系＋⊆T×T对所有的活动变迁对（x，y）有x≻y且y≻x，则称x，y是排他序关系，记作x＋y。

定义5［6］（交叉序） （N，［i］）是一个工作流系统，交叉序关系‖⊆T×T对所有的活动变迁对（x，y）有x≻y且y≻x，则称x，y是交叉序关系，记作x‖y。

结合上面介绍的3种行为关系，下面给出正规的行为轮廓的概念。

定义6［6］（行为轮廓） 对一个工作流系统（N，［i］），行为关系集 BP＝｛→，＋，‖｝作为网（N，［i］）的行为轮廓。

为了确定网中2个变迁之间的关系，给出下面图例，分别说明行为轮廓的几种关系。图a所示严格序关系，严格序关系说明2个变迁必须都发生，从初始标识开始的所有发生序列中A的发生必然引起B的发生，记作A→B。图b所示的排他序关系，说明在所有的发生序列中A和B都不会在同一条发生序列中，或者A和B在同一发生序列中都不会出现，记作A＋B。图c说明的交叉序关系，说明在一个发生序列中，A和B可以以任何序列存在。因此，交叉关系可以导致循环结构，记作A‖B。

因为有源模型和目标模型，存在变迁对之间的对应关系，下面给出基于行为轮廓的对应关系定义。

定义7［1］（对应关系） 2个工作流系统（N1，［i1］）和（N2，［i2］），通过2组活动变迁对之间的对应关系，即～⊆T1×T2，∀（tx，ta），（ty，tb）∈～，若对任意的t1∈T1，那么存在t2∈T2使得t1～t2，（tx，ty）⇒（ta，tb）。

由于目标模型的改变通过行为轮廓表现出来，根据模型与模型之间的对应关系，可以找出目标模型的变化域。

定义8［1］（变化域） 给定流程模型petri网BP＝（S，T，F，C），若变化部分为BP1＝（S1，T1，F1，C1）则BP1是BP的一个子模块，即S1∈S，T1∈T，F1∈F，C1∈C，BP1⊆BP。

在文献［1］和文献［3］中，给出了其他的一些定义可以参考，这里就不具体介绍了。

2 根据petri网动态行为寻找变化域

基于petri网及行为轮廓来分析业务流程中变化部分，来寻找源模型的变化域，由于静态寻找变化域的约束和限制，把流程模型抽象成流程模型的petri网，分析源模型和目标模型的对应关系。确定最初的可疑变化区域W，最终找出流程模型的变化域。

为了寻找流程模型的变化域，从petri网出发，根据行为轮廓确定目标模型的变化域W0，

寻找目标模型的变化域W0。

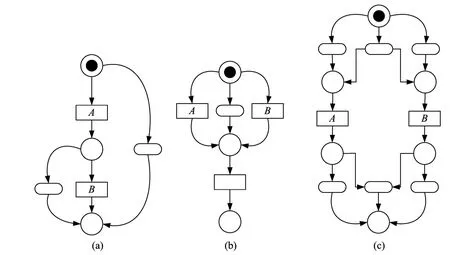
图1 行为轮廓关系图

输入：BP1＝（S1，T1，F1，C1），源模型

BP0＝（S0，T0，F0，C0），目标模型

输出：W0，变化区域

1）将源模型和目标模型转化为petri网结构；

2）根据定义9得到的可疑区域W1，依次标出节点a1a2a3∧an-1an，对应的源模型中的区域W′1；

3）从a1（an）开始考虑它与下一个（上一个）节点的行为关系，若满足严格序（严格逆序）关系，那么a1（an）就不是可疑节点，从而可从区域中去除，若不满足，那么它就是可疑节点；

4）若出现分支结构时，选取一个与源模型比较，看是否满足严格序或严格逆序关系，再根据第3判断；若出现交叉和排他序关系，再回到2）；根据上述判断可以得到变化域W0，然后输出变化区域W0和可疑节点集U。

3 实例分析

3个人出去旅游，有3种做法：（1）3个人能相邻而坐（也就是坐在一块）；（2）2个人能相邻而坐，另1个人不相邻；（3）3个人都不相邻。怎么坐才能最优？不言而喻，最优的情况就是让3人能坐在一块。当3个人坐在一块不能满足时，这时再考虑次优情况，2个人坐在一块而另一个人不能坐在一块。当次优的情况也不能满足时，最后考虑都不相邻。

为了更加清楚明了，如下所示：

其中，火车座位安排如下：

为了计算怎么样才能出现3个人相邻、能让2个人相邻、都不相邻3种情况，不妨让座位号对5求余。

从上面可以看出：

第1种情况：3个人相邻。若对5求余的余数是3，4，0的就证明3个座位挨在一块。如：（3，4，0）；

第2种情况：2个人相邻。若从对5求余的3，4，0中抽出3，4或4，0，再从1，2中抽出1个；要不就是1，2在一块，从3，4，0中抽出1个这是2个座位挨在一块。

如：（3，4），1 （3，4），2 （4，0），1 （4，0），2（1，2），3 （1，2），4 （1，2），0；

第3种情况：都不相邻。都不相邻这种情况较多在这里就不一一叙述。在这里若3个人相邻仅限于3张座位号相邻，不相邻的不考虑；若2个人相邻仅限于其中2相邻的座位号相邻。

图2是针对买票所建立起来的流程图，糅合了顾客、售票中心以及支付中心3个对象在内，由于各自特征不同，在实际中该模型是不易操作的，所以在考虑各自的特征后且满足3者需要的前提下，构建一个目标模型，使它与源模型一致，就得到图3所示的目标模型。

图2 源模型

图3 目标模型

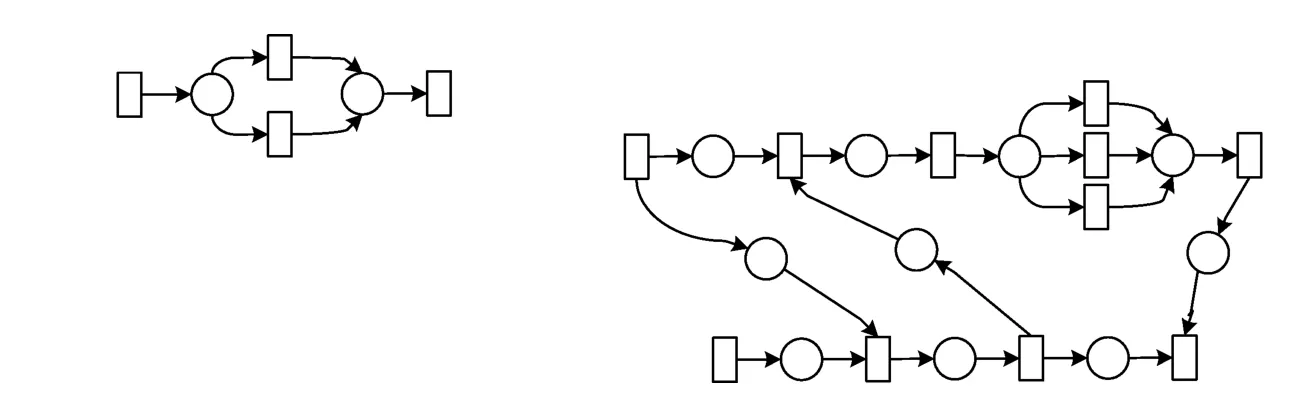
图4 变化域

而火车实际的座位安排如下：

第1种情况：3个人相邻。

X3 X4 X5或者 X6 X7 X8 在这里X＝0，1，2，…

第2种情况：2个人相邻。

X1 X2或者 X9 X10（在这里X与0前面的数字相加，如X＝1，则1＋1＝2，那么数字就是19 20。

X3 X4另一个不是X5；X4 X5另一个不是X3；X6 X7另一个不是X8；X7 X8另一个不是X6。

第3种情况：3个人都不相邻。这种情况较多在这里不再讨论。不过仍然用上面的图件来表示和解决。

该实例是用3个人的情况，达到最优的是让3个人坐在一块，其中笔者分析的这种情况相对来说是最简单的，以后不管是3个人相邻还是多个人相邻，用到的道理和分析方法都是一样的，在这就不再分析了。

4 结语

变化域是业务流程的关键问题，所以寻找变化域在业务流程中关系具有一定的现实意义。本文基于Petri网行为轮廓理论寻找变化域，在分析业务流程对应活动变迁的基础上提出了寻找业务流程变化域的方法，首先通过实际的业务流程得到流程模型Petri网，再根据行为轮廓分析模型Petri网，并画出源模型，随后根据源模型与目标模型之间的一致性及相对活动变迁之间的对应关系，找出疑似变化点并分析模型的疑似变化域，最后用行为轮廓确定最小变化域。在本文给出的实例中也证明了该方法的有效性。

寻找业务流程的变化域在现实中有很大的应用价值，所以笔者计划将其运用到流程模型中寻找变化域，从而改进模型，使模型更加优化，希望能在不久的将来开发和完善一套先进的操作系统使得寻找变换域与优化模型一体化。由于它的应用范围广泛，希望这个想法很快能够实现。

［1］Matthias Weidlich，Mahias Weske，Jan Mendling．Change Propagation in Process Models Using Behavioural Profiles：Service Computing．Potsdam 2009［C］．Bangalore：IEEE Conference Publications，2009：33-40 ［10．1109／SCC．2009．58］．

［2］吴哲辉．Petri网理论［M］．北京：机械工业出版社，2006．

［3］Xianwen Fang，Wenjun Hao．The Approach of Analyzing the Smallest Change Domain in Process Models based on Petri Nets［J］．Applied Mathematics and Information Sciences，2012，6（3）；943-949．

［4］Matthias Weidlich，Artem Polyvyanyy，Nirmit Desai et al．Process Compliance Analysis based on Behavioural Profiles［J］．Information Systems，2011，36（7）：1009-1025．

［5］Matthias Weidlich，Jan Mendling，Mathias Weske．Efficient Consistency Measurement based on Behavioural Profiles of Process Models［J］．Software Engineering，2011，37（3）：410-429．

［6］袁崇义．Petri原理与应用［M］．北京：电子工业出版社，2005．

［7］Sergey S，Matthias W，Jan M．Business Process Model Abstraction based on Behavioral Profiles［C］．Editor：Paul P．Sth International Conference，ICSOS 2010．San Francisco，2010：1-16．

［8］Matthias Weidlich，Jan Mendling，Mathias Weske．Propagating Changes between Aligned Process Models based on Petri Nets［J］．Applied Mathematics and Information Sciences，2012，6（3）：943-949．