考虑摩擦热的弹塑性平面接触应力及塑性应变分析＊

李鹏阳，陈 欢，王世军，王权岱，傅卫平

（1．西安理工大学 机械与精密仪器工程学院，西安710048；2．重庆大学 机械传动国家重点实验室，重庆400044）

摩擦热引起的热应力对相互接触且相对运动零件的失效有很大的影响（例如，刹车片的热破裂，齿轮的变形）．一个接触的零件通常受到表面机械力和热应力两种类型的载荷作用，前者主要包括正压力和切向力，后者主要是由摩擦热引起的热应力［1］．研究热应力场和机械应力场对了解零件的失效有很重要的意义．文献［2］利用有限元法对考虑温度影响的接触表面热弹塑性问题进行了研究；文献［3］研究了层状材料热弹塑性接触问题；文献［4］应用有限元对刚性球与平面接触且相对运动时的摩擦热问题进行了研究．近年来，半解析法在接触问题上获得了广泛的应用，文献［5］利用半解析法建立了二维热弹塑性接触模型；文献［6］将其扩展到了三维，并研究了接触热对弹塑性平面接触的影响．文 献 ［7］应 用 快 速 傅 氏 变 换 （Fast Fourier Transformation，FFT）和共轭梯度法（Conjugate Gradient Method，CGM）建立了热弹性和热弹塑性接触模型；文献［8］应用半解析热弹塑性接触模型研究了热效应对接触表面压力分布和米塞斯应力的影响；文献［9］用数值法建立热弹塑性接触模型．文献［10］运用有限元研究了不同变形特性下考虑摩擦热时接触压力与接触面积的变化规律；文献［11］利用有限元建立三维模型对耦合瞬态温度场进行了仿真研究；文献［12］应用数值算法研究了干接触体滑动过程中的温度场问题；文献［13］研究了材料属性热变化对弹塑性接触问题的影响；文献［14-15］考虑表面粗糙度和塑性变形，对微接触点的稳态温升、瞬态温升进行了分析研究；文献［16-17］应用有限元法对结合面接触问题模型进行了研究；文献［18］对接触中的刚度问题进行了研究；文献［19］建立了受扭矩作用下的刚性球与平面接触模型，并对其进行了深入研究；文献［20］研究了一种涂层表面和圆柱体表面、粗糙表面的弹塑性接触，并分别与其均匀密化解进行比较．然而，目前对考虑热因素接触摩擦的研究相对比较少．

文中考虑摩擦热对接触的相关热效应影响，应用FFT和CGM求解球与平面的接触问题，对接触表面温度分布以及不同摩擦热对接触表面压力分布、表面下塑性应变区域和表面下米塞斯应力场的影响进行研究，为分析材料失效和寿命提供理论依据．

1 热应力场模型的建立

当刚性球与弹塑性表面接触并做相对运动时，接触区域内一点q（x，y，0，t）在表面下一点g（x，y，z，t）处引起的温升和法向热位移分别为T（x，y，z，t）和ui（x，y，z，t），t为时间，如图1所示，图1中Vs为相对滑动速度．

为了对研究问题进行简化，本文做如下假设：①整个摩擦过程满足库伦摩擦定律，且摩擦因数保持不变；②接触过程中的摩擦能全部转换为热能，并作为热流源，且认为上接触体和接触区域以外的接触面全部为绝热的；③两接触物体都为各向同性材料，且其热参数不会随温度变化．

图1 刚性球与弹塑性平面接触示意图Fig．1 The description of contact of rigid ball with elastic-plastic plane

瞬间热传导的解耦和偏微分控制方程与准静态热弹性变形量为

其中Vs为相对滑动速度．

表面温度边界条件为

当由热引起的法向位移量计算出来后，由FFT和CGM求出接触法向弹性位移和法向残余位移量［19］，CGM数值算法首先计算考虑热膨胀应变的塑性应变增量，然后计算残余位移增量，求解残余表面位移并和前一步的残余表面位移量进行比较，重复这个过程直到残余位移增量收敛．塑性应变、温度、载荷、接触压力、残余表面位移以及硬化参数则分别增加一定增量形成一个新的初始条件以进行下一步加载步骤，直到最终算法收敛，得出最终计算结果．接触表面总的位移量u为

式中：u（n）为法向弹性位移量；u（r）为法向残余位移量；u（t）为法向热位移量．

由法向位移量可算出接触表面压力分布，涉及到接触的非线性，确定弹塑性接触压力需要用迭代数值算法［21］，即Polonsky-Keer共轭梯度法．表面热流量为

式中：uf为接触表面法向位移量；p为接触表面压力．最后求出热应力场分布．

2 刚性球与弹塑性平面接触

算例模型选择刚性球与弹塑性平面接触，且做匀速运动，只考虑刚开始瞬间，相关参数见表1．

表1 基本参数和材料参数Tab．1 The basic parameters and material parameters

文中对计算结果分别进行了无量纲化．坐标系通过x／a、z／a无量纲化，a为赫兹接触半径；压力p和应力σ则分别通过p／pmax和σ／σY无量纲化，其中pmax为最大接触压力，σY为初始屈服强度．

2．1 不同滑动速度下接触表面温度分布

为了研究不同滑动速度下接触表面上的温度分布情况，取摩擦系数始终为0．2，滑动速度Vs分别为5m·s-1、10m·s-1、20m·s-1，其相应速度下接触表面的温度分布如图2所示．

图2 接触表面温度分布Fig．2 The temperature distribution of contact surface

由图2看出，接触表面温度的大小随着滑动速度的增加而增加，且最高温度点的位置随着滑动速度的升高慢慢向滑动速度方向偏移．这是因为滑动速度增大，摩擦热输入也增大，表面温度会升高．同时，滑动速度的方向对温度场也有影响．

2．2 考虑摩擦温升对材料热效应影响下接触表面压力的分布

为了研究接触体材料屈服应力受摩擦热影响下的弹塑性接触问题，取摩擦热输入fs为0．15 W·m-2的条件下，分别取摩擦系数f为0．1和0．4，图3给出了在考虑和不考虑摩擦温升对材料热效应影响下接触表面压力的分布．

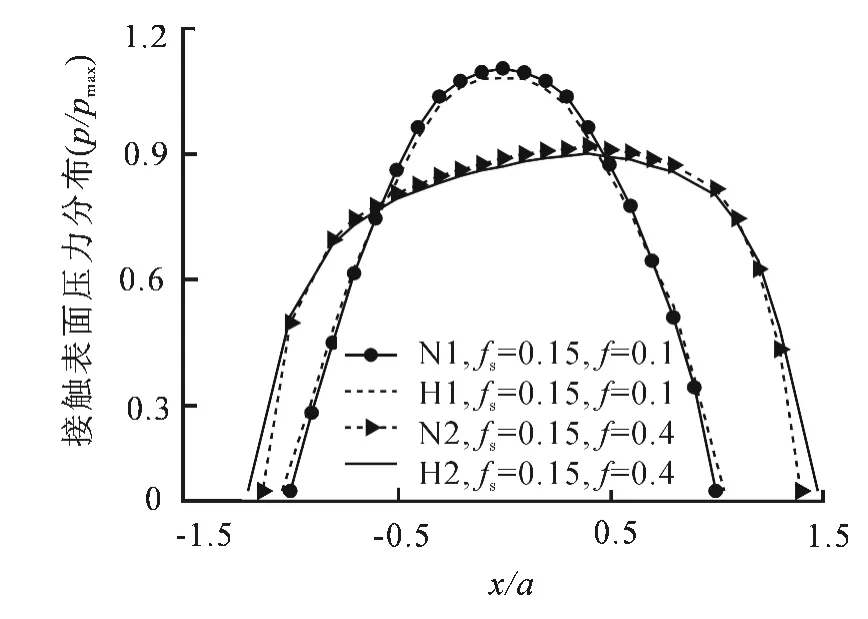
图3 接触表面压力的分布图Fig．3 The distribution of contact surface pressure

图3中N1、N2表示不考虑热影响，H1、H2表示考虑热影响．由图3可知，在考虑温度相关效应后，由于表面摩擦热作用使接触体温度升高而屈服应力降低，材料将会出现软化现象，接触压力的最大值比不考虑温度相关的情况有所减小，接触面积也相对增加．说明忽略温度相关效应将高估最大接触压力而低估相应外载荷下产生的接触面积．

2．3 不同滑动速度下接触表面的压力分布

为了研究不同滑动速度下接触表面的压力分布，本文设定摩擦系数为0．2，滑动速度Vs分别为5m·s-1、10m·s-1、20m·s-1，其相对应速度下接触表面的压力分布如图4所示．

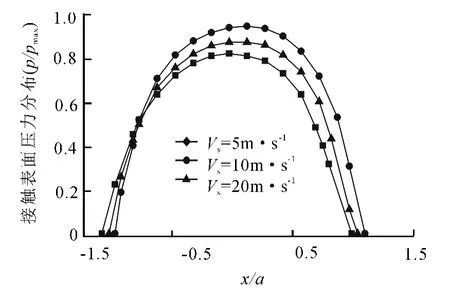
图4 不同滑动速度下表面压力分布Fig．4 The surface pressure distribution at different sliding velocity

由图4可知，当滑动速度较低的时候，接触压力近似关于x／a＝0轴对称，接触表面的最大压力随着滑动速度的增加而增加，并且接触压力的分布向滑动速度方向发生偏转，这是由于摩擦热的增加导致了接触压力进而发生了扭曲变形．

2．4 塑性应变区域和米塞斯应力的变化

为了研究摩擦热对塑性应变区域和米塞斯应力σvm的影响，保持摩擦系数为0．2、压强为定值，分别取滑动速度Vs为5m·s-1和15m·s-1，塑性应变ξ以百分比的形式进行表示．图5和图6分别为不同摩擦热对塑性应变和米塞斯应力的影响．

由图5～6可知，塑性应变区域和米塞斯应力随着表面热流的增加逐渐向接触表面延伸，并且塑性核中心区域向滑动方向有一定的偏移，这是因为摩擦热使表面下温度分布不均匀，导致最大塑性区域向速度滑动方向表面移动，由此可见，当摩擦热大到一定程度的时候，热应力对总米塞斯应力的影响将不能忽略．

图5 x-z面的塑性应变ξ分布Fig．5 The plastic strain distribution on x-zsurface

图6 x-z面的米塞斯应力分布（σvm／σY）Fig．6 Mises stress distribution on x-zsurface

2．5 最大米塞斯应力的变化

为了研究摩擦热对接触体最大米塞斯应力的影响，保持摩擦系数为0．2，取滑动速度Vs分别为0，5，10，15，20，25m·s-1，图7为不同滑动速度对最大米塞斯应力的影响．

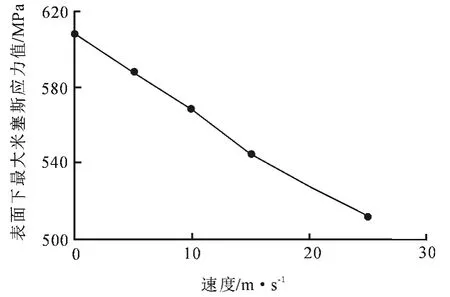
图7 不同滑动速度对最大米塞斯应力的影响Fig．7 Effect of different sliding speed on maximum Mises stress

由图7可知，最大米塞斯应力值随滑动速度的增大而减小．这是因为随着滑动速度输入的增加，接触体温升增加，相应的屈服应力减小，最大米塞斯应力也随着减小．因此，忽略温度相关效应的影响则高估了材料的强度性能．

3 结 论

文中考虑摩擦热对接触的相关热效应影响，应用FFT和CGM对球与面接触建立热弹塑性接触模型，对接触表面温度分布以及不同摩擦热对接触表面压力分布、表面下塑性应变区域和表面下米塞斯应力场的影响进行了研究，具体结论为

1）接触表面温度的大小随滑动速度的提高而升高，且最高温度点的位置随滑动速度的提高缓慢向滑动速度方向偏移．

2）在考虑材料屈服应力温度相关效应后，接触表面压力最大值比不考虑温度相关效应的时候减小，而接触面积相对有所变大．

3）接触表面的最大压力随着滑动速度的增加而增加，并且接触压力的分布向滑动速度方向发生偏转，这是由于摩擦热的增加导致了接触压力发生了扭曲变形．

4）随着摩擦热的增加，接触体内的最大应力值越来越小，且塑性应变区域和米塞斯应力随着表面热流的增加逐渐向接触表面延伸，且向滑动方向有一定的偏移．

［1］ LIU S，WANG Q．Transient Thermoelastic Stress Fields in a Half-Space［J］．Journal of Tribology，2003，125（1）：33．

［2］ GUPTA V，BASTIAS P，HAHN G T．Elastic-Plastic Finite-Element Analysis of 2-D Rolling-Plus-Sliding Contact with Temperature Dependent Bearing Steel Material Properties［J］．Wear，1993，169：251．

［3］ YE N，KOMVOPOULOS K．Effect of Residual Stress in Surface Layer on Contact Deformation of Elastic-plastic Layered Media［J］．Journal of Tribology，2003，125（4）：692．

［4］ OVCHARENKO A，YANG M，CHUN K，et al．Transient Thermo Mechanical Contact of an Impacting Sphere on a Moving Flat［J］．Journal of Tribology，2011，133：031404．

［5］ GONG Z，KOMVOPOULOS K．Mechanical and Thermomechanical Elastic-plastic Contact Analysis of Layered Media with Patterned Surfaces［J］．Journal of Tribology，2004，126（1）：9．

［6］ LIU G，WANG Q，LIU S．A Three-Dimensional Thermo Mechanical Asperity Contact Model for Two Nominally Flat Surfaces in Contact［J］．Journal of Tribolog，2001，123：595．

［7］ LIU S，WANG Q．A Three-Dimensional Thermomechanical Model of Contact Between Non-Conforming Rough Surfaces［J］．Journal of Tribology，2001，123（1）：17．

［8］ BOUCLY V，NELIAS D，LIU S B，et al．Contact Analyses for Bodies with Frictional Heating and Plastic Behavior［J］．Journal of Tribology，2005，127（2）：355．

［9］ CHEN W W，KIM W，WANG Q．Transient Thermomechanical Analysis of Sliding Electrical Contact of Elastic-Plastic Bodies［J］．Journal of Tribology，2009，131：021406．

［10］ 黄健萌，高诚辉．粗糙面变形特性对摩擦温度与接触压力的影响［J］．农业机械学报，2012，43（4）：202．HUANG Jian-meng，GAO Cheng-hui．Influence of Deformation Characteristic of Rough Surface on Frictional Temperature and Contact Pressure［J］．Transactions of the Chinese Society for Agricultural Machinery，2012，43（4）：202．（in Chinese）

［11］ 赵凯辉，魏朗．鼓式制动器三维热-机耦合温度场仿真［J］．农业机械学报，2009，40（2）：32．ZHAO Kai-hui，WEI Lang．3DThermo-Mechanical Coupling Temperature Field Simulation of Drum Brake［J］．Transactions of the Chinese Society for Agricultural Machinery，2009，40（2）：32．（in Chinese）

［12］ 陈辉，胡元忠，王慧，等．干接触体滑动过程温度场的计算［J］．清华大学学报：自然科学版，2008，19（18）：2231．CHEN Hui，HU Yuan-zhong，WANG Hui，et al．Calculation of Temperature Fields of Bodies in Sliding Contact Without Lubrication［J］．Journal of Tsinghua University：Science and Technology，2008，19（18）：2231．（in Chinese）

［13］ 佟瑞庭，刘更，刘天祥．材料属性温度相关热弹塑性接触问题研究［J］．中国机械工程，2007，47（11）：1962．TONG Rui-ting，LIU Geng，LIU Tian-xiang．Study on Thermal Elasto-Plastic Contact Problems with Temperature-Dependent Properties［J］．China Mechanical Engineering，2007，47（11）：1962．（in Chinese）

［14］ 田红亮，朱大林，秦红玲．两弹性接触粗糙低速滑动表面温升的分形模型［J］．三峡大学学报：自然科学版，2010，32（2）：65．TIAN Hong-liang，ZHU Da-lin，QIN Hong-ling．Fractal Model of Temperature Rise Between Two E-lastic Contact Rough Slow Sliding Surfaces［J］．Journal of China Three Gorges University：Natural Sciences，2010，32（2）：65．（in Chinese）

［15］ 田红亮，朱大林，秦红玲．两弹塑性非赫兹接触粗糙表面温升的分形模型［J］．三峡大学学报：自然科学版，2010，32（4）：77．TIAN Hong-liang，ZHU Da-lin，QIN Hong-ling．Fractal Model of Temperature Rise Between Two E-lastoplastic Nonhertz Contact Rough Surfaces［J］．Journal of China Three Gorges University：Natural Sciences，2010，32（4）：77．（in Chinese）

［16］ 尤晋闽，陈天宁．结合面静态接触参数的统计模型研究［J］．振动与冲击，2010，29（11）：47．YOU Jin-min，CHEN Tian-ning．Statistical Model for Static Contact Parameters of Joint Surfaces［J］．Journal of Vibration and Shock，2010，29（11）：47．（in Chinese）

［17］ 尤晋闽，陈天宁．结合面静摩擦系数的统计模型［J］．振动与冲击，2010，29（12）：26．YOU Jin-min，CHEN Tian-ning．Statistical Model of Static Friction Coefficient Between Joint Surfaces［J］．Journal of Vibration and Shock，2010，29（12）：26．（in Chinese）

［18］ 刘意，刘恒，易均，等．塑性接触层的法向接触刚度等效方法［J］．振动与冲击，2010，32（7）：43．LIU Yi，LIU Heng，YI Jun，et al．Equivalent Method for Normal Contact Stiffness Considering Plastic Contact Layer［J］．Journal of Vibration and Shock，2010，32（7）：43．（in Chinese）

［19］ LI P Y，WANG Z J，LI X Y，et al．Elasto-Plastic Indentation of a Half-Space by a Rigid Sphere under Normal and Torque Loading［J］．Tribology International，2013，33（62）：141．

［20］ 金赛英，刘更，佟瑞庭，等．自适应无网格方法在涂层弹塑性接触中的应用［J］．机械科学与技术，2010，29（11）：1564．JIN Sai-ying，LIU Geng，TONG Rui-ting，et al．Application of Adaptive Meshless Method in Elasto-Plastic Contact Analysis for Layered Surfaces［J］．Mechanical Science and Technology for Aerospace Engineering，2010，29（11）：1564．（in Chinese）

［21］ POLONSKY I A ，KEER L M．A Numerical Method for Solving Rough Contact Problems Based on the Multi-Level Multi-Summation and Conjugate Gradient Techniques［J］．Wear，1999，231：206．