PWM技术中载波对输出电压影响的分析

方成辉，姜凯文

（上海海事大学 物流工程学院，上海201306）

0 引 言

逆变器在电力电子领域占据着重要的地位，它的主要作用就是把直流电压或者电流转化成期望频率和幅值的交流电压或电流。逆变器的调制技术决定了输出波形的质量，好的调制策略具有输出电压的谐波少、逆变器的开关次数少、逆变器的控制简单等优点。目前常用的两种调制方式是载波调制PWM策略和空间矢量脉宽调制策略（SVPWM）。

载波调制PWM法是一种利用调制波与载波的比较结果来决定逆变器输出电平的方法，其中调制波一般采用正弦波，为提高直流侧的电压利用率，可以往正弦波中注入三次谐波，载波一般采用三角波或者锯齿波［1］。近年来，多位学者在PWM技术中的载波方面做了大量研究，例如载波移相调制［2－4］、随机脉宽调制［5，6］等。

本文将详细分析单H桥及多H桥的情况下载波相位对输出电压的影响，并观察变载波频率调制下输出电压的频谱分布。

1 载波的相位移动对输出电压的影响

载波调制PWM技术的基本原理是通过正弦调制波与三角波或锯齿波的比较确定开关的触发脉冲。本文选取三角波做为载波，下面将具体分析载波的相位移动对输出电压产生的影响。

1．1 一个H桥的情况下载波相位对输出电压的影响

当逆变电路中只包含一个H桥，且以两电平的方式运行时，相应的仿真电路模型如图1所示。

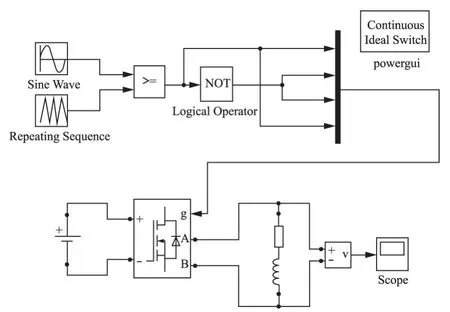
图1 两电平逆变器仿真电路

仿真电路参数设置：直流侧电压Udc＝100 V，调制比M＝0．9，基波频率ω0＝50 Hz，载波频率ωc＝1 500 Hz，设定当载波的初相角为0时，载波的电压值为负的峰值，仿真结果如图2所示。

利用图1的仿真电路模型，载波每次相移45°角进行一次仿真，对每次的仿真输出波形做FFT分析，将得到的仿真数据列入表1。

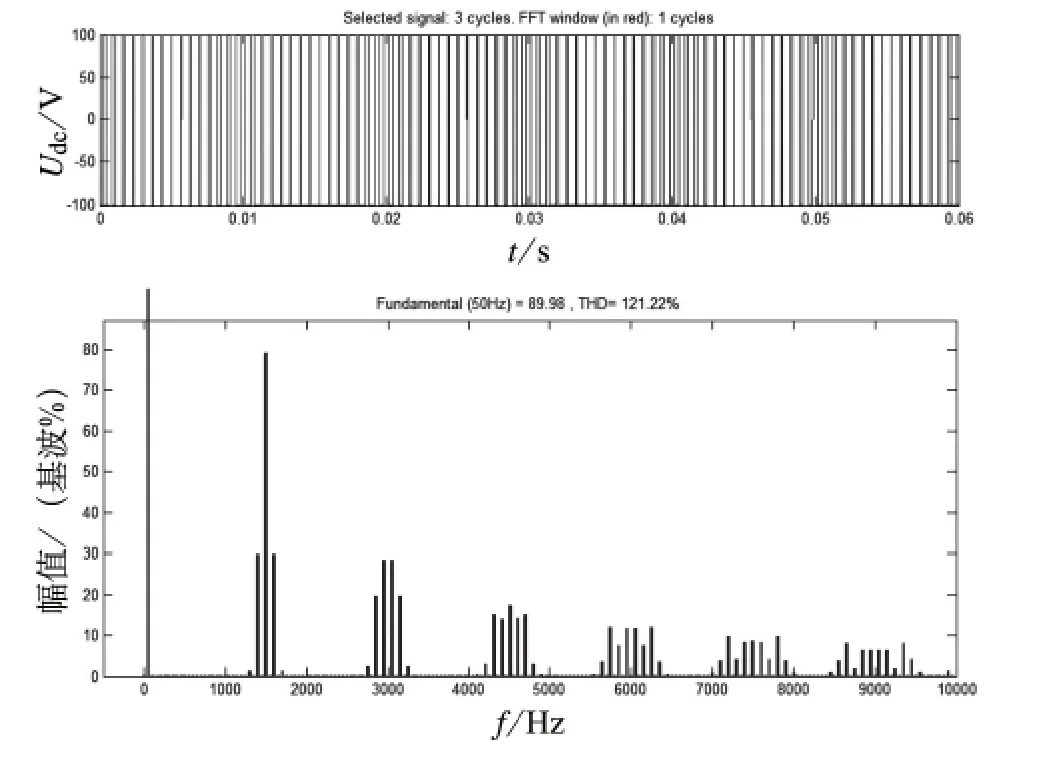
图2 一个H桥情况下逆变器的输出电压波形及频谱分布（载波初相角为0）

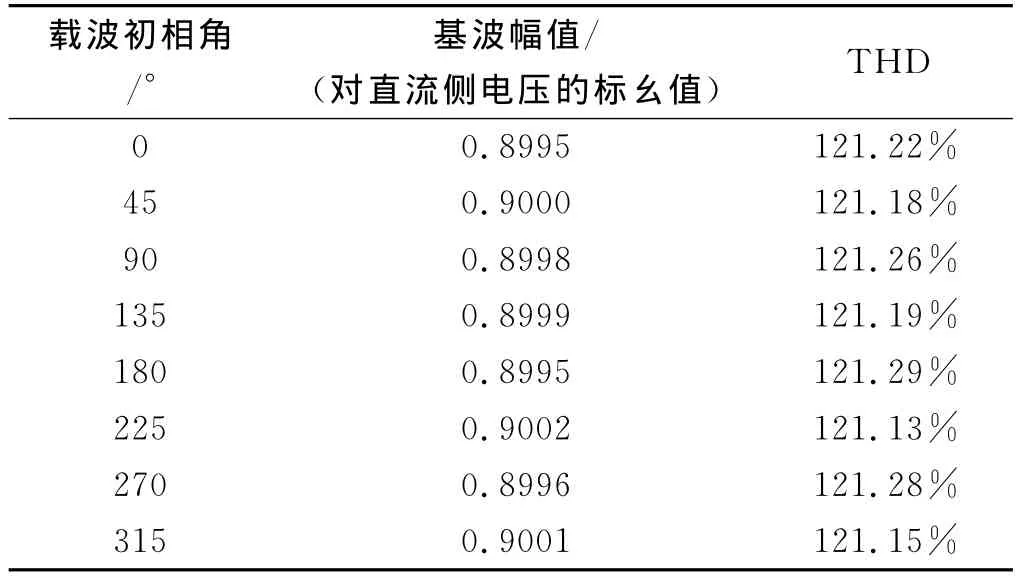
表1 载波相移对输出电压的基波和THD的影响（一个H桥）

由表1的数据可知，在只有一个H桥的情况下，载波的相移对输出电压的基波幅值和THD的影响可以忽略。

1．2 多个H桥的情况下载波相移对输出电压的影响

一个H桥在两电平方式运行情况下的输出电压的傅里叶级数表达式为

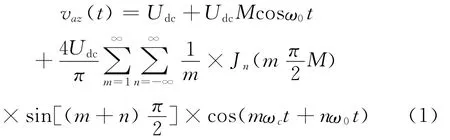
式中，Jn（x）为贝塞尔函数；ω0为调制波角频率；ωc为载波角频率；正弦调制波的初相角设置为0。由式（1）可知，若每个H桥的载波以2（i－1）×180／N（i为 H桥的序号，N为H桥的个数）的方式进行移相，则输出相电压的高于N次载波谐波及所有低于N次的载波谐波及其边带谐波将被消除。这个结论与多电平PSCPWM调制策略（H桥采用两电平调制）的结论相吻合。仿真结果如图3、图4所示，仿真数据如表2所示。

由表2可以看出，在多个H桥的情况下，采用载波相移方式可以显著减小输出电压的谐波畸变率。

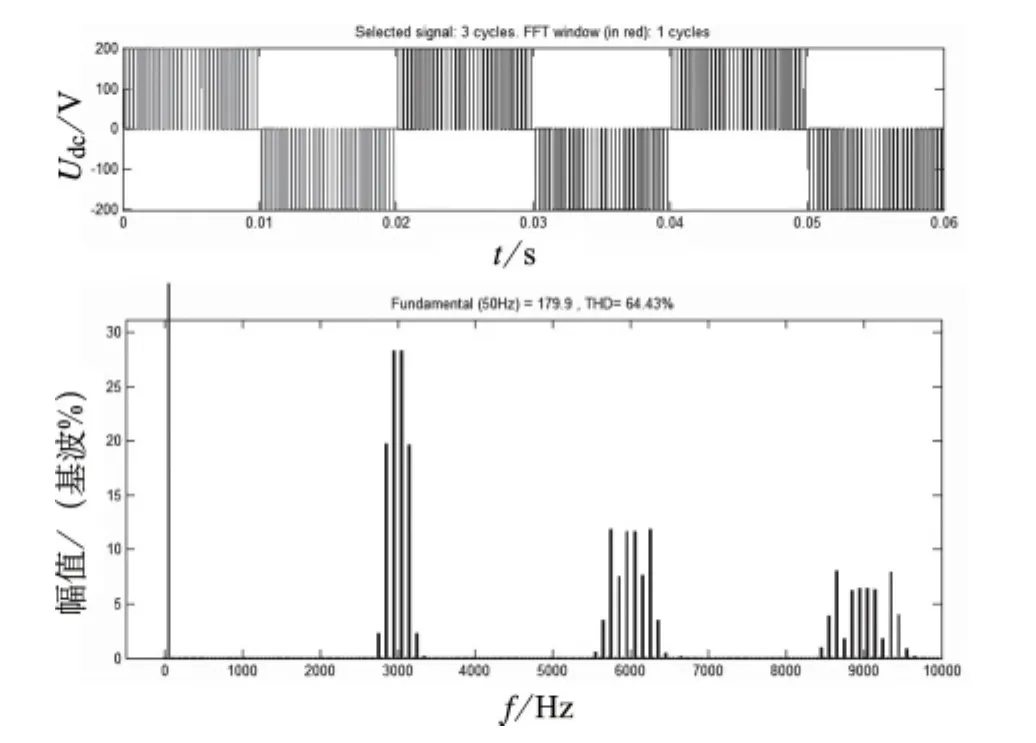
图3 两个H桥情况下逆变器的输出电压波形及频谱分布

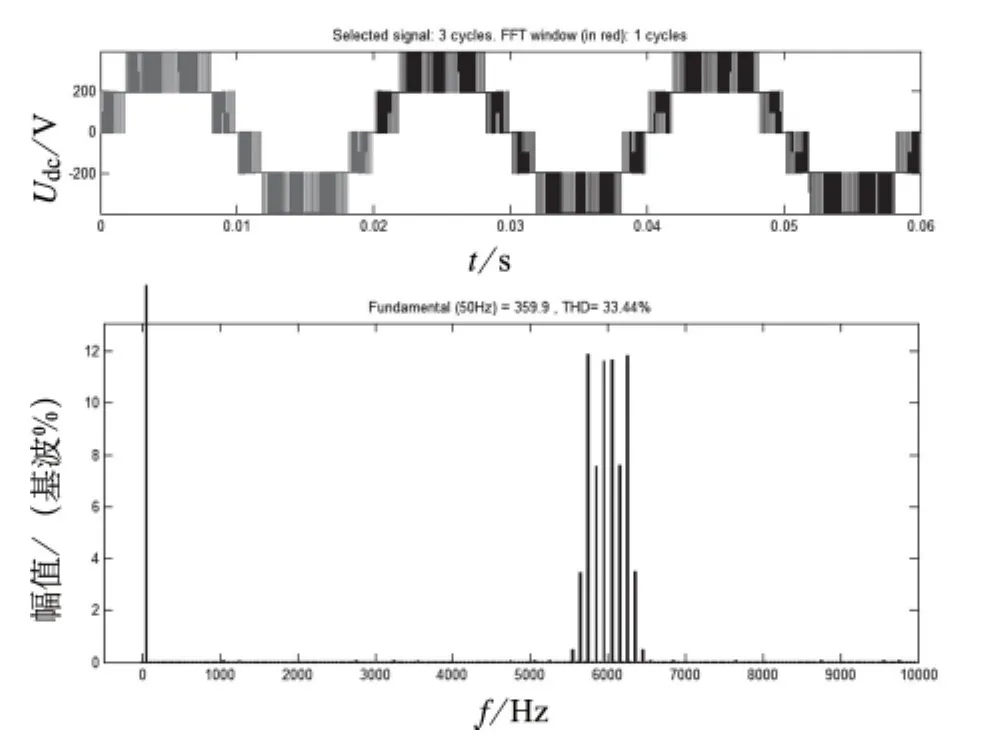
图4 四个H桥情况下逆变器的输出电压波形及频谱分布

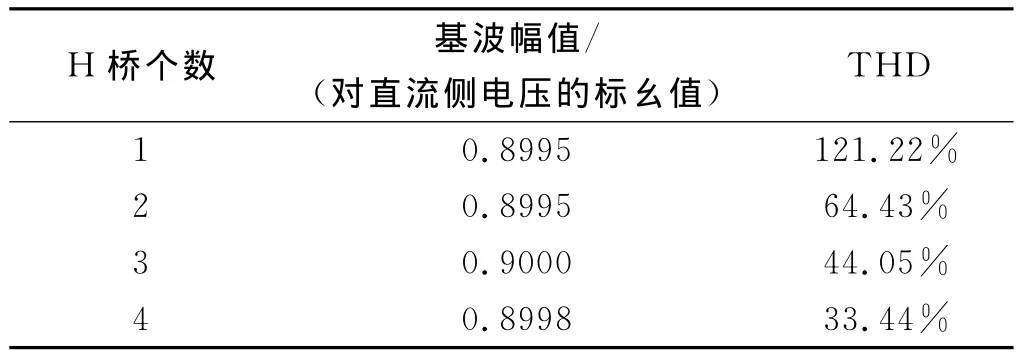
表2 载波相移对输出电压的影响（多H桥）

2 载波变频对输出电压的影响

由以上分析可知，用载波调制PWM策略调制出输出电压的谐波主要集中在n次（n＝1，2，3，……）载波频率处。因此，要改变输出电压的频谱分布可以通过改变载波频率来实现。要使谐波在频率轴上的分布尽量均匀，可以在一个基波周期内采用变载波频率的方式进行调制。

两个载波频率交替调制的仿真电路模型如图5所示。

仿真电路参数设置：直流侧电压Udc＝100 V，调制比M＝0．9，基波频率ω0＝50 Hz，载波频率ωc1＝1 500 Hz，ωc2＝3 000 Hz。ωc1、ωc2的作用时间比为1∶1，仿真结果如图6。当ωc1、ωc2的作用时间比为3∶7时，仿真结果如图7。

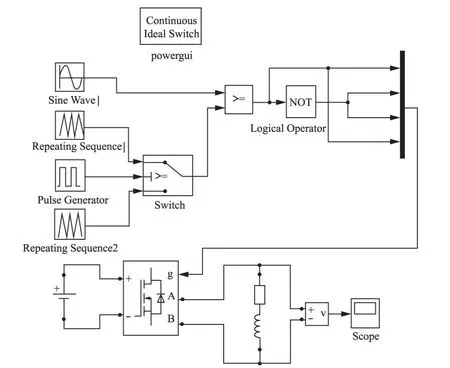
图5 两个频率交替调制的仿真电路模型

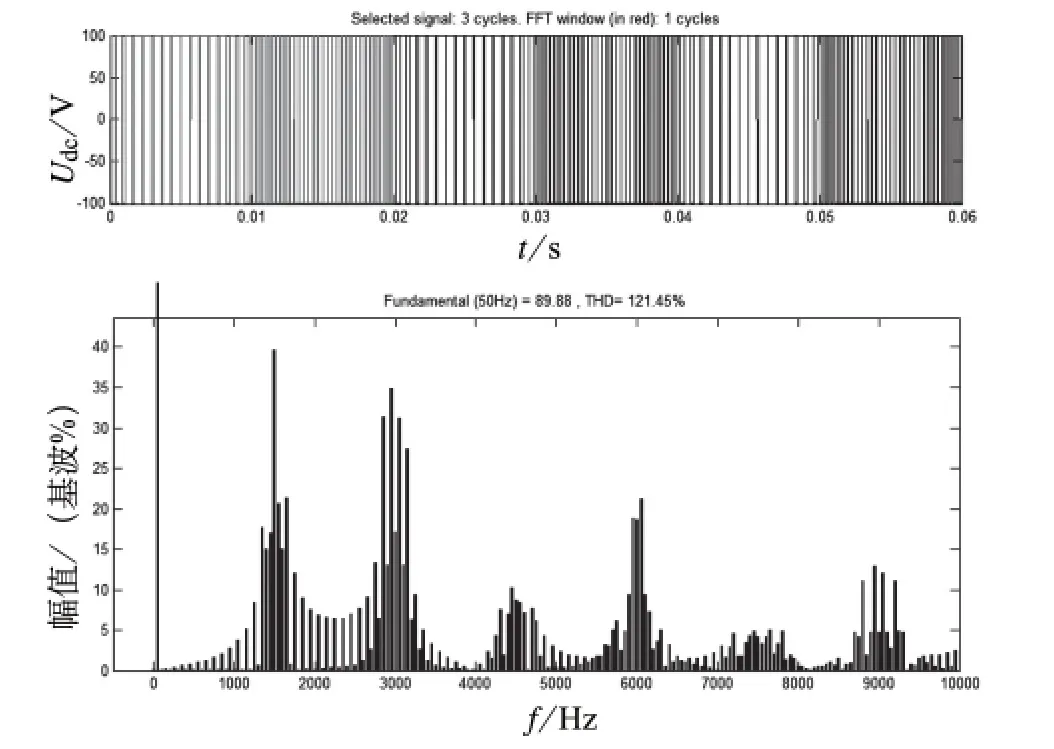
图6 ωc1、ωc2作用时间比为1∶1时的输出电压及谐波频谱

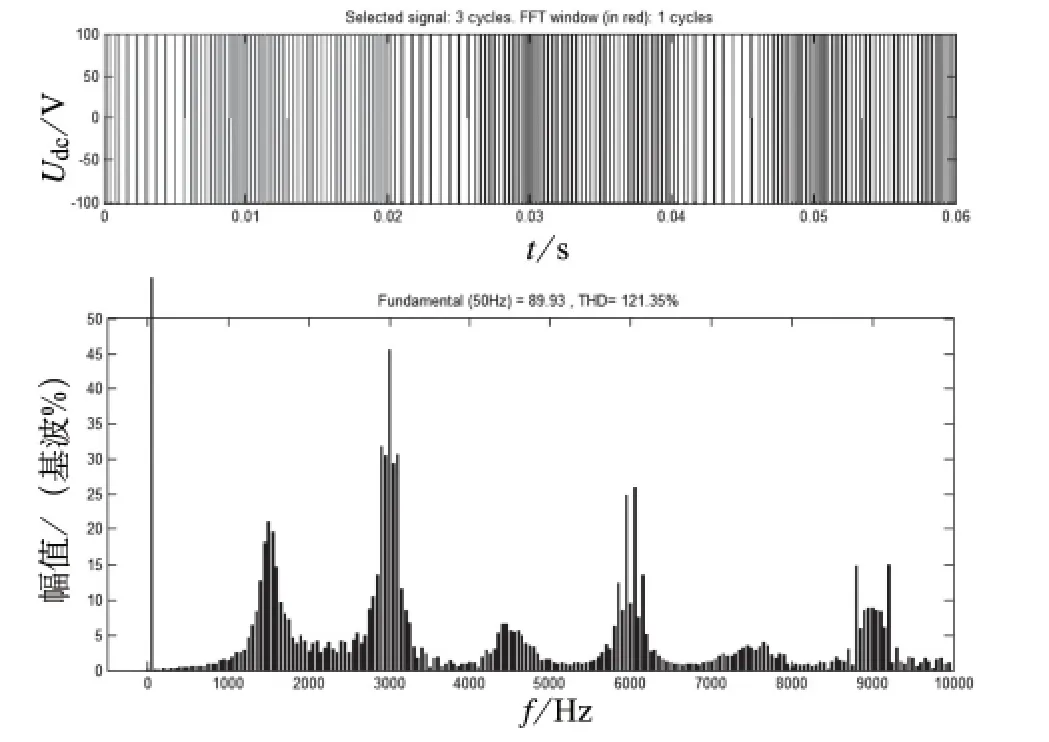
图7 ωc1、ωc2作用时间比为3∶7时的输出电压及谐波频谱

当采用三个频率的载波交替调制时，仿真结果如图8，取ωc1＝1 500 Hz，ωc2＝3 000 Hz，ωc3＝4 500 Hz，其余参数同上，ωc1、ωc2、ωc3的作用时间之比取1∶1∶1。

由图6、图7、图8可以看出，某一载波频率的作用时间越长，该频率处的谐波幅值就越大，一个基波周期内包含载波频率的个数越多，频谱分布越均匀。

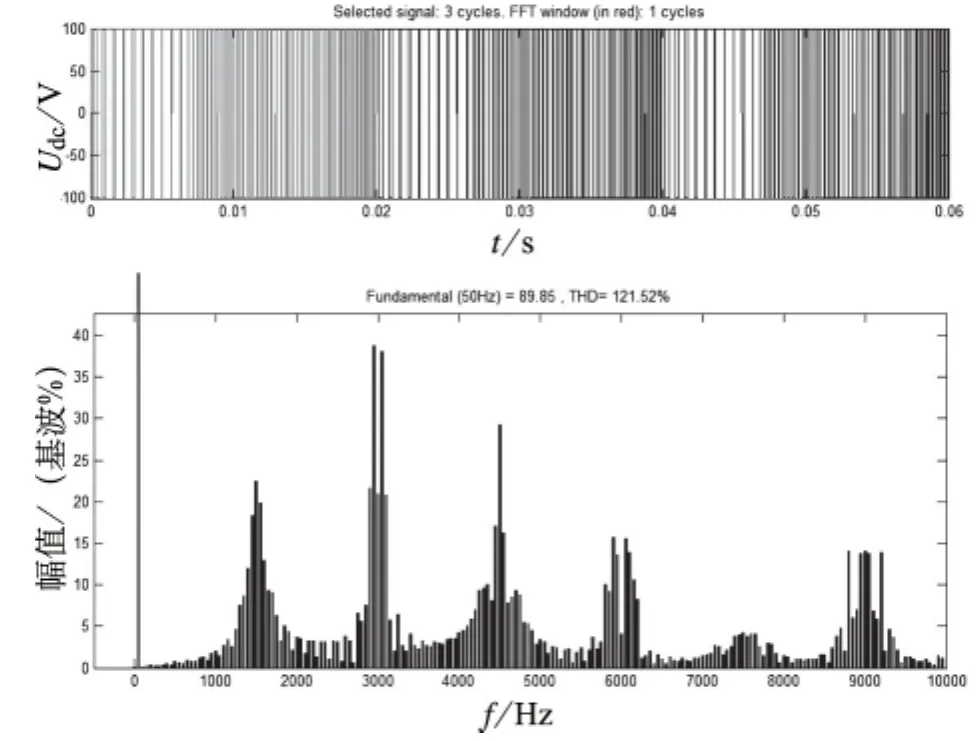
图8 ωc1、ωc2、ωc3的作用时间之比为1∶1∶1时的输出电压及谐波频谱

3 结 论

本文详细分析了载波相位对输出电压的影响，通过载波移相叠加方式调制出的输出电压在谐波畸变率方面有很大的改善。

本文研究了变载波频率调制对输出电压频谱的影响，通过在一个基波周期内改变载波的频率可以使输出电压频谱分布更加均匀。实际应用中，电压频谱越均匀，系统的电磁兼容性越好。当输出电压的谐波频率与机械设备的固有频率相同时，常常会产生噪声干扰，对设备的运行带来不利影响，使电压频谱均匀化可以削弱特定频率谐波的幅值，降低这种不利的影响。通过Matlab／Simulink软件的仿真结果验证了结论的正确性。

［1］ Holmes D G，Lipo T A．Pulse Width Modulation for Power Converters：Principle and Practice［M］．A John Wiley ＆Sons，2003．

［2］ Rabinovici R，Baimel D，Tomasik J，Zuckerberge A．Thirteen－level cascaded H－bridge inverter operated by generic phase shifted pulse－width modulation［J］．Power Electronics，IET，2013，6（8）：1516－1529．

［3］ Naderi R，Rahmati A．Phase－Shifted Carrier PWM Technique for General Cascaded Inverters［J］．Power Electronics，IEEE Transactions on，2008，23（3）：1257－1269．

［4］ Zhao H，Guo Y．Research of four quadrant cascaded high voltage frequency converter based on carrier phase shifting PWM［C］．Transportation，Mechanical，and Electrical Engineering（TMEE），2011 International Conference on，2011：1125－1128．

［5］ 幸善成，吴正国．基于多电平随机脉宽调制技术的共模电压和谐波抑制方法［J］．中国电机工程学报，2006，26（17）：57－61．

［6］ 李 辉，吴正国．采用随机脉宽调制技术降低电力有源滤波器开关谐波［J］．电工技术学报，2010，25（8）：105－115．