光伏发电跟踪支架阴影数学模型研究
2015-01-01特变电工新疆新能源股份有限公司何银涛张梅黄华
特变电工新疆新能源股份有限公司 ■ 何银涛 张梅 黄华
0 引言
阴影遮挡是影响光伏发电的主要因素之一,因此,GB 50797-2012《光伏发电站设计规范》要求[1],光伏方阵间距设置要保证在全年每天9:00~15:00(当地真太阳时)时段内相邻支架不互相遮挡。光伏发电跟踪支架相比于固定式支架,发电量有明显提高[2],但其阴影变化情况更加复杂。目前,针对跟踪支架的控制系统精度和效率方面的研究较多[3,4],对于跟踪支架运行过程中阴影的变化研究较少,而这一研究对于科学合理地设置相邻跟踪支架排布间距有重要意义。
本文根据特变电工哈密863实验电站中3种常用跟踪支架的运动规律,建立跟踪支架阴影数学模型,从而为科学合理地确定相邻跟踪支架排布间距、高效利用土地资源提供理论依据。
1 建立跟踪支架数学模型
根据跟踪支架运动规律,建立适当的坐标系,并分别给出组串平面4个角点在运动范围内的轨迹方程,进而得到跟踪支架位置的数学模型。
1.1 平单轴跟踪支架
图1为平单轴跟踪支架的俯视图和左视图。建立如图1b所示坐标系o-xyz,其中,z轴垂直于xoy平面。平单轴跟踪支架转动轴与水平面平行,南北向布置,东西向转动,ox指向正西方向,oz指向正北方向;A1-D1和A2-D2为AD转动范围内的两个任意位置,θ为跟踪转角;o点离地面的距离为H,L为组串长度,2R为组串宽度。

图1 平单轴跟踪支架结构简图
根据平单轴转动规律,D点轨迹可表示为:

A、B、C 3点的坐标和D点关系式为:

根据以上关系式可求得A、B、C、D 4点在坐标系o-xyz中的坐标,即得到平单轴位置数学模型。
1.2 斜单轴跟踪支架

图2 斜单轴跟踪支架结构简图
图2为斜单轴跟踪支架的前视图,组串平面与水平面垂直。建立如图2所示坐标系o-x1y1z1,x1轴垂直于y1oz1平面。斜单轴跟踪支架转动轴与水平面夹角α,且转动轴南北向布置,东西向转动;oz1沿转动轴方向,oy1轴沿AD边指向上方;转动轴低端离地面的距离为H1,高端离地面高度为H2;L为组串长度,2R为组串宽度。
根据布尔莎-沃尔夫转换模型[5],对坐标系o-x1y1z1进行一次坐标变换,即绕y1轴逆时针旋转角度α,得到坐标系o-xyz,变换关系用矩阵形式表示为:

变换后得到的坐标系o-xyz与图1b中平单轴的坐标系一致。则在坐标系o-xyz中,D点轨迹表示为:

A、B、C 3点的坐标和D点关系式为:

再根据式(3)变换关系就可求得A、B、C、D在坐标系o-x1y1z1中坐标(xli, yli, zli),其中i=A、B、C、D,即得到斜单轴位置数学模型。
1.3 双轴跟踪支架
图3为双轴跟踪支架的结构简图,组串平面ABCD为矩形。建立如图3所示坐标系o-xyz,ox指向正东方向,oz指向正南方向;o点离地面的距离为H;L1为BC长度,L2为AB长度;双轴跟踪支架在跟踪时间范围内,组串表面时刻与太阳光线垂直。

图3 双轴跟踪支架结构简图
双轴支架绕y轴转动跟踪太阳方位角,绕x轴转动跟踪太阳高度角,组串平面ABCD初始位置在xoz平面内,BC平行于x轴,AB平行于z轴。设在跟踪过程中,转动一个位置便建立新的坐标系o-xiyizi,且BC平行于xi轴,AB平行于zi轴,则o-xiyizi可通过坐标系o-xyz坐标变换获得。在坐标系o-xiyizi中,A、B、C、D坐标表示为:
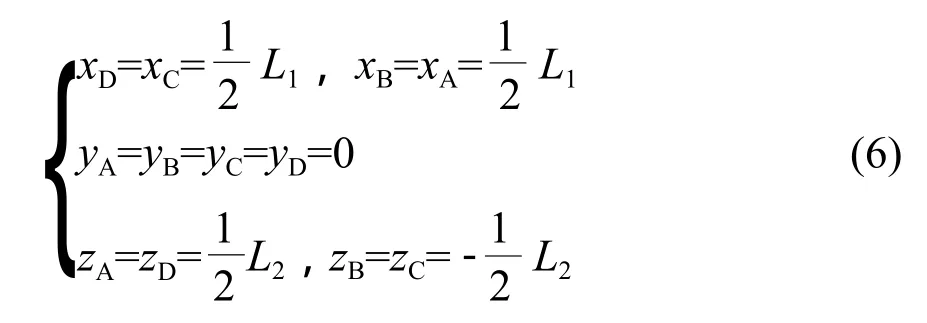
设某一时刻太阳高度角h,太阳方位角β,则双轴转动过程可表示为:先绕y轴转动γ,再绕x轴转动,β=90°-h。故根据布尔莎-沃尔夫转换模型[5],坐标变换关系表示为:

2 阴影数学模型
遮挡物高度与其阴影长度的几何关系表示如图4所示(以A点为例,点A′为A点在地面的影子)。

图4 遮挡物高度与其阴影长度的几何关系图
2.1 平单轴跟踪支架
根据图1b和图4几何关系,遮挡物高度表示为:HGi=yi+H,则阴影长度Li=HGicoth,阴影长度南北向分量LNSi=|Licosγ|,阴影长度东西向分量LEWi=|Licosγ|,其中,i=A、B、C、D。则A、B、C、D4 点在地面的影子 A′、B′、C′、D′的坐标表达式为:

式中,i=A、B、C、D。
2.2 斜单轴跟踪支架
参照图4几何关系,遮挡物高度表示为:HGk=y1k+H1,k=A、D;HGj=y1j+H2,j=B、C。阴影长度Li=HGicoth,阴影长度南北向分量LNSi=|Licosγ|,阴影长度东西向分量LEWi=|Lisinγ|,其中,i=A、B、C、D。则A、B、C、D 4点在地面的阴影 A′、B′、C′、D′的坐标表达式为:

式中,i=A、B、C、D。
2.3 双轴跟踪支架
参照图4几何关系,遮挡物高度表示为:HGi=yi+H,阴影长度Li=HGicoth,阴影长度南北向分量LNSi=|Licosγ|,阴影长度东西向分量LEWi=|Lisinγ|,其中,i=A、B、C、D。则A、B、C、D 4 点在地面的阴影 A′、B′、C′、D′的坐标表达式为:

式中,i=A、B、C、D
3 计算示例
以阴影变化情况最为复杂的斜单轴为例,对光伏发电跟踪支架阴影数学模型的计算过程进行说明。
如图2所示,已知L=10.1 m,R=1.8 m,H1=1.3 m,H2=3.9 m,α=15°;方位角跟踪范围为-45°≤θ≤45°;建设地为哈密地区,纬度 42.6°,经度94.9°;并假设地面平整。
冬至日真太阳时9:00,斜单轴跟踪角度θ=-45°,根据1.2节内容及式(3)可得D点在坐标系o-x1y1z1中坐标为:

同理可得:

根据太阳角计算公式[6],建设地(纬度42.6°,经度94.9°)冬至日真太阳时9:00,太阳高度角h=12°,方位角γ=41.56°,再根据2.2节内容,可得:
HGA=1.23+1.3=2.53 m,LA=2.53 cot12°=11.9 m,LNSA=|11.9cos41.56°|=8.9 m,LEWA=|11.9sin41.56°|=7.9 m。则根据式(9),A点在地面阴影A′ 坐标为:

同理可得:
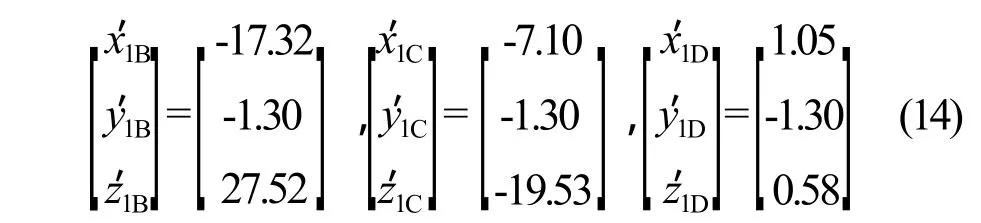
通过以上计算过程,可得到斜单轴组串在冬至日真太阳时早9:00的姿态(式(11)和式(12))和对应的阴影情况(式(13)和式(14))。

图5 斜单轴跟踪支架排布及阴影俯视图
相邻斜单轴组串的阴影形状相同,只要保证相邻斜单轴组串在地面阴影不重叠,便不会产生遮挡现象,故由几何关系可得邻近4个斜单轴组串排布状况及阴影状况如图5所示。蓝色框表示斜单轴组串的俯视图,黑色框表示对应的阴影;设置的东西向间距为7 m,南北向间距18.5 m。
以上是斜单轴的计算示例。平单轴、双轴计算过程与之类似。
4 结束语
本文建立了3种常用光伏跟踪支架的阴影数学模型,并以斜单轴跟踪支架的阴影数学模型为例,对此阴影数学模型的计算过程进行说明,得到了斜单轴在冬至日真太阳时早9:00的位置坐标和阴影坐标;最后,根据几何关系,得到了合理的斜单轴方阵布置间距,保证整个跟踪范围内既不产生相互遮挡现象,又能充分利用土地。
因此,此阴影数学模型对设置光伏跟踪支架排布的合理间距、优化跟踪支架方阵占地面积有重要的指导意义。
[1] 中国电力企业联合会. GB 50797-2012光伏发电站设计规范[M]. 北京: 中国计划出版社, 2012.
[2] 张峰, 王垚, 陈正安, 等. 光伏电站跟踪系统的技术分析和比较[A]. 中国电机工程学会清洁高效燃煤发电技术协作网2009年会论文集[C], 2009, 1-6.
[3] 张相明, 邓玮, 关焕新, 等. 光伏发电双轴自动跟踪控制系统的设计[J]. 东北电力技术, 2013, 3: 48-50
[4] 张鹏飞. 光伏发电自动跟踪系统的设计[D]. 哈尔滨理工大学, 2009, 23-24
[5] 张宏. 布尔莎-沃尔夫转换模型的几何证明[J]. 测绘与空间地理信息, 2006, (2): 52-53.
[6] (西 )Antonio Luque, (美 )Steven Hegedus, 等 [著 ], 王文静 ,李海玲, 周春兰, 等[译]. 光伏技术与工程手册[M]. 北京: 机械工业出版社, 2011.
