不同纬度下光伏电站阴影的影响与分析
2015-01-01云南省电力设计院陈祥汪玉华
云南省电力设计院 ■ 陈祥 汪玉华
1 光伏阵列阴影计算
依据GB 50797-2012《光伏发电站设计规范》,光伏阵列间距的计算以“保证光伏阵列冬至日日照时长6 h/天”为目标(即保证冬至日6 h日照。下文中“保证冬至日光伏阵列的日照时长”简称为“日照时长”),并提供如下公式:

式中,L为光伏阵列倾斜面长度,m;D为光伏阵列南北方向两排阵列间距离,m;β为光伏阵列倾斜面倾角,( °);φ为当地纬度,( °)。
目前国内不同纬度建设的地面光伏电站,均依据式(1)完成光伏阵列间距的计算,未考虑因纬度、日照时长的不同,光伏阵列距离变化所引起的辐射量及发电量折减;同时也未考虑该变化引起光伏电站占地面积、投资的差异。
本文将针对上述情况进行研究,并分析由此引起的发电量损失和投资变化之间的关系,提出不同纬度光伏电站建议采用的日照时长。
为此推导出式(2),用于计算各纬度下不同日照时长的光伏阵列间距:

式中,d=Lcosγ/tgα[1],其中,γ为太阳方位角,( °),α 为太阳高度角,( °)。
2 各约束条件的能量损失
2.1 各纬度的理论辐射值
不同纬度下地外天文辐射(天文辐射)为:
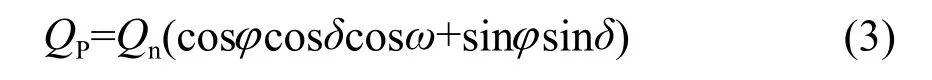
式中,QP为逐时水平面理论辐射值,W/m2;Qn为逐日地外辐射值,W/m2;φ为当地纬度,( °);δ 为太阳赤纬角,( °);ω 为太阳时角,( °)。
其中:

式中,Qsc为太阳常数,W/m2,取1367;n为一年中的日期序号。

Qn的计算若采用式(4),误差为±3.3%;采用式(5),误差为±0.01%[2]。本文计算采用式(5)。
地外天文辐射经大气衰减后到达地面,其中直接辐射为[3]:

式中,Qb为逐时水平面直接辐射值,W/m2;α 为太阳高度角,( °)。

式(9)~(11)中A为场址海拔,km,本文计算统一采用0.5。
同时,到达地面的散射辐射为:

式中,Qd为逐时水平面散射辐射值,W/m2。

于是,可得地外天文辐射经大气衰减后的地面总辐射为:
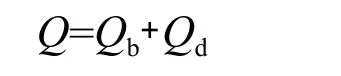
式(8)~(13)均采用经验公式,其在不同地区应用时存在差异,本文主要研究能量吸收与纬度、日照时长的比例关系,为方便计算结果的对比,上述参数因均采用海拔值为0.5 km,故均相同。
2.2 光伏阵列倾斜面理论发电量
光伏阵列为提高发电量,均以一定角度朝向赤道。Liu等[4]认为,倾斜面上接收的太阳总辐射由3部分组成:直接辐射、散射辐射、地面反射辐射,即:

式中,QT为倾斜面接收的总辐射;QT,b为倾斜面接收的直接辐射;QT,d为倾斜面接收的散射辐射;QT,r为倾斜面接收的地面反射。
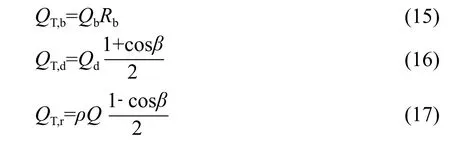
式中,ρ为地表物体表面反射率,本文计算统一采用25%。
对于北半球朝向赤道的倾斜面,式(15)中Rb为:
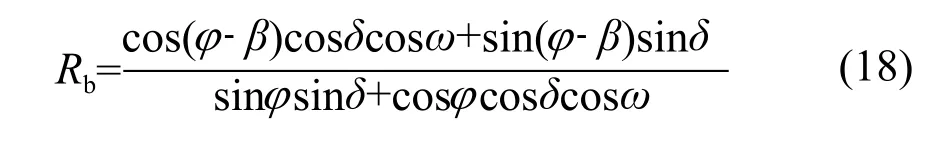
3 各约束条件引起的参数变化
本文首先依据式(2)推算不同日照时长条件下全年逐天光伏阵列被遮挡的时段,再依据式(3)~(13)计算出全年逐天水平地面接收的辐射量,最后结合式(14)~(18)得出光伏阵列倾斜面全年可利用辐射量率(即可发电量率),见表1。

表1 各约束条件下光伏电站可发电量比例
同时,依据式(2)可得上述约束条件下的光伏阵列间距,从而得到光伏电站单位MWp占地面积。因占地面积的变化将引起光伏电站部分材料投资变化(例如:电缆投资)、土地费用变化等。
为简化投资变化的计算,光伏电站造价取值原则如下:
1)电站除因占地引起的设备、材料投资变化外,其他投资不变;2)光伏组件单价取4.5元/Wp、逆变器单价取0.5元/Wp,其他材料价格均参考电力定额价格;3)不考虑因地形变化引起的投资变动;4)土地征占按照有偿、无偿两种方式分别计算,土地价格取0.5万元/亩(一亩约为666.67 m2)。
在完成上述计算后,将各约束条件的计算值以日照时长6 h(09:00~15:00)的相应值作为基准值进行归一化,得图1及图2。

图1 不同纬度各参数变化趋势
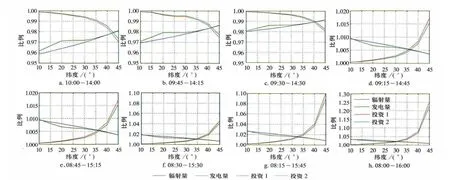
图2 不同日照时长各参数变化趋势
4 结论分析与讨论
结合表1、图1和图2,分析上述计算结果,可得如下结论:
1)日照时长不同的条件下,低纬度地区电站可利用辐射值比例、可发电量比例变化显著;而高纬度地区电站可利用辐射值比例、可发电量比例变化不明显,且低纬度地区电站投资差异较小,高纬度地区电站投资差异显著。可看出随着纬度增高引起电站占地面积增大,导致电站投资显著增加。
2)日照时长相同的条件下,高纬度地区电站可发电量比例均高于低纬度地区。电站可发电量比例与纬度呈正相关。
3)纬度低于25°时,可发电量比例的增加高于投资比例的增加;反之,纬度高于30°时,投资比例的增加高于可发电量比例的增加。故建议低纬度地区光伏电站的日照时长增至7~8 h,高纬度地区的日照时长则应减至6 h以下。
4)而纬度介于25°~30°时,在日照时长为6~7 h情况下,投资比例的增加与发电量的比例的增加基本一致。故建议此时日照小时数可取 6~7 h。
5)由图2分析得知,随着日照时长的增大,可发电量比例曲线与投资比例曲线的交点向低纬度偏移。由此得出各纬度的最佳日照时长曲线,如图3所示。
以建设在纬度40°的光伏电站为例,日照时长取6 h:理论上电站可发电率为99.19%,电站占地28.47亩(约18980 m2);如按照图3中日照时长取5 h:理论上电站可发电率为99.67%,电站占地25.58亩(约17053.3 m2)。电站可发电率减少0.48%,电站占地面积减少2.89亩(约1926.67 m2,10.15%)。按照上文提到的的造价原则,电站按照土地有偿、无偿的方式,分别减少投资约8.57万元(10.13%)、7.13万元(10.13%)。可见,光伏电站选取最佳日照时长后效益显著。
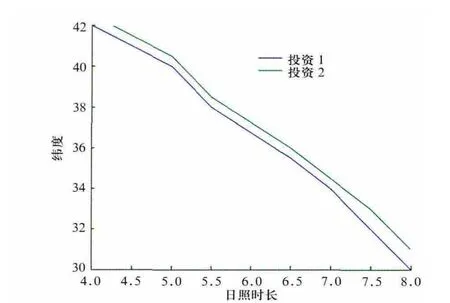
图3 各纬度的最佳日照时长
综上所述,光伏电站阵列间距的计算应依据纬度、投资水平的不同进行分析并论证。如该地区已有实测光资源数据,还应结合光资源数据进行分析,以期达到节约土地、控制投资、提高电站收益的目的。
[1] 杨金焕, 于化丛, 葛亮. 太阳能光伏发电应用技术[M]. 北京: 电子工业出版社, 2009, 25-26.
[2] Duffie J A, Beckman W A. Solar engineering of thermal processes[M]. New York: John Wiley & Sons, 1991.
[3] Hottel H C. A simple model for estimating the transmittance of direct solar radiation through clear atmospheres[J] Solar Energy,1976, 18(2): 129-134.
[4] Liu B Y H, Jordan R C. The interrelationship and characteristic distribution of direct, diffuse and total solar radiation[J]. Solar Energy, 1960, 4(3): 1-19.
