锥面联接的压入受力分析及其仿真

姜薛起，李锡文

（华中科技大学 机械科学与工程学院，湖北 武汉 430074）

0 引言

在机械设备中，有诸多使用锥形轴伸来传递扭矩的联接结构，有的甚至还要承受弯矩等复杂工况。圆锥过盈联接是锥形轴伸的核心，它不仅具有普通圆柱过盈联接的结构简单、定心性好、承载力高等优点［1］，还有易于控制过盈量或结合压力、拆装方便且配合面不易擦伤［2］、高转速下承受交变扭矩更为可靠［3］等特点。因此，圆锥过盈联接广泛应用于机床主轴、刀柄联接、轴承、联轴器、化工装备、特殊工具等［4］场合。

在锥形轴伸联接的设计当中，可以采用多种方法，如：将锥形轴等效成圆柱过盈配合，采用图算法［5］；或将锥面压力视作均布，在弹性范围内进行理论计算［6］；或采用有限元方法进行仿真分析。无论采用哪种方法，都需要过盈量或结合压力的保证，压入过程恰是关键。

1 锥面联接的压入受力分析及计算

某设备悬臂搅拌轴上的锥面联接如图1所示。该锥面联接主要用于扭矩传递，并保证一定的刚度。锥孔轴1（含法兰）和联接法兰3为40Cr合金钢，锥轴2为SUS 321不锈钢，2和3之间为螺纹联接。两法兰通过均布的N个螺栓联接拉紧，并可拆卸。配合锥面的小端和大端直径分别为Φ50mm、Φ60mm，配合长度为L＝100mm，即锥度C＝1∶10。

锥面联接传递扭矩，主要是由联接面间结合压力产生的静摩擦力传递的。为了计算简便，需假设以下前提：①在锥面联接的整个配合面上的结合压力为常量；②应力在弹性范围内，无塑性变形；③配合面的周向摩擦符合库仑摩擦定律。

用dm表示配合圆锥面大、小两端的平均直径，将结合压力产生的摩擦力转化为在圆周半径上的作用力Ft，如图2所示。将圆锥面圆周分布的结合压力p转化为某一轴向剖面上的直接作用力，如图3所示。其中，Fa为通过螺栓对锥轴施加的轴向压入力，Fa1为使锥套保持平衡所需的作用力，Fn为锥面结合压力的等效作用力，Ff为压入过程的摩擦阻力，α为半锥角，配合锥形面小端和大端结合直径分别为d1和d2，等效直径为dm＝（d1＋d2）/2。

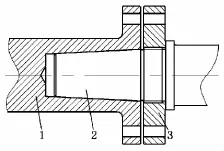
图1 锥面联接结构示意图

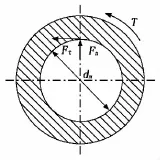
图2 扭矩传递模型

设μ为锥面结合面传递扭矩时的静摩擦因数，则Ft＝Fnμ，又Fn＝pA，对此联接圆锥，结合面积A＝πdmL/cosα，摩擦力所能传递的扭矩为T＝Ftdm/2。考虑到配合面的接触率等因素，综合取一定的安全系数［n］，可得锥面间结合力和传递扭矩的关系为：

式（1）中的半锥角α仅在角度很大的一些非自锁式联接中需要考虑，其余情况下可以忽略。

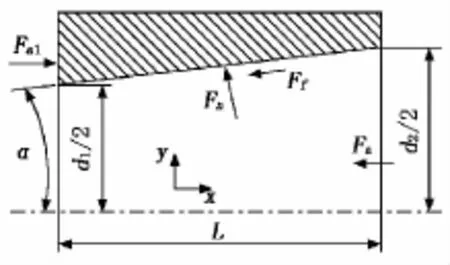
图3 压入过程锥孔轴受力分析

由外锥套在x方向受力平衡，得：

又由于Ff＝μiFn，其中μi为锥面结合面压入过程中的动摩擦因数，若令μi＝tanρ，则ρ为当量摩擦角，代入式（2）可得：

即

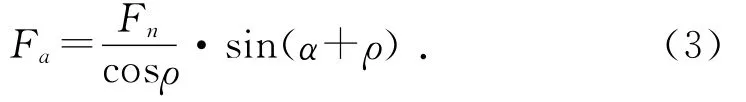
由式（1）、式（2）、式（3）可得到锥面间结合压力与压入力的关系为：

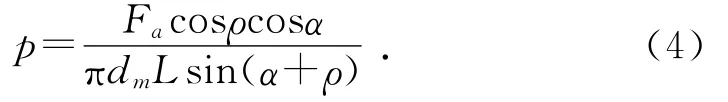
此锥面传递扭矩为940Nm，由于结构参数已知，取摩擦因数μ＝0.12，μi＝0.10，则ρ＝5.71°，取安全系数［n］＝1.5，可计算得圆锥面间结合力p＝24.71 MPa，圆锥轴压入力Fa＝64.01kN。

2 有限元仿真分析

选择ANSYS Workbench中的接触工具，通过对锥轴施加压入力，对此圆锥轴伸联接的压入作用进行仿真，仿真得到锥面间结合压力，从而初步判定锥面轴伸联接承载能力是否达标。

首先在SolidWorks中建立模型。考虑到对称性，为了计算简便，取1/4模型进行分析，并将外锥轴与法兰的螺纹联接视作整体，且忽略法兰螺纹孔。通过中间格式导入ANSYS Workbench的Static Structural模块，采用Sweep方式划分网格。

接下来，设置材料弹性模量及泊松比和强度。之后添加约束和载荷。考虑到实际中是在两法兰上采用螺栓预紧施加压入力，故选择锥孔上靠近小端侧法兰面为固定支撑约束面；由于本模型是取1/4进行分析，为还原问题的对称性，在模型两个零件的两垂直剖面均设置为光滑无摩擦的对称面。在锥轴所在法兰右侧面添加压入力，考虑到1/4模型，添加压入力载荷16.0kN。外锥面和内锥孔面分别设置为接触面和目标面，接触类型为摩擦，摩擦因数为0.10。接触类型为非对称行为，求解器为Normal Lagrange。求解后所得锥面结合压力分布情况如图4所示。

对锥孔轴来说，周向应力和径向应力在沿半径方向均在内孔处有最大值，提取在锥孔整条母线上的等效范式应力，如图5所示。

3 结果分析与讨论

3.1 配合面上的压力分布

由图4可看出，在整个结合面上的压力分布显然不是均匀一致的，在两端由于应力集中等因素导致结合压力偏高，尤其是在锥孔大端更为明显。在锥孔轴（包容件）锥面结合起始处很短的一段内结合压力略大，约为30MPa；在较长的定直径段上结合压力较为稳定，约为17MPa～22MPa；在锥孔轴法兰段内，结合压力增大，约为30MPa～40MPa；最后，在锥面结合的大孔边缘处，由于应力集中等因素，结合压力从40MPa激增到120MPa。综合整个结合面来看，考虑不同段内的结合压力和结合面积占比，可认为圆锥结合面上的加权结合压力约为25MPa，这与前述理论计算值基本吻合。

图4 锥面结合压力分布

图5 锥孔沿母线等效应力

理论计算未考虑结合面上压力分布的不均匀性，仿真却可以直观地将其表现出来。当然，包容件上法兰外径引起的变化也是引起压力分布不均的因素，如果采用油压结构，应当避免包容件在配合段上的外径突变。实际使用中，锥孔大端是较为容易出现裂纹等损伤的部位，这与仿真相吻合，故压力分布不均在应用中需要考虑。若采用图算法，可得平均直径下圆柱过盈的结合压力约为15MPa～20MPa，这小于前述理论计算值和仿真值，是因为计算中考虑了1.5倍的安全系数。

3.2 锥孔内侧沿轴向的范式等效应力分布

由图5可知，起始处为锥孔底过渡处，应力也略大，故形成了起始处等效应力下凹的曲线。综合考虑轴向、周向和径向应力（主要是后两者），得到锥孔内部的等效范式应力约为45MPa，在接触面边缘均偏大，尤其是在锥孔大端的边缘处达到125MPa，可见应力分布的不均匀性。故此处应倒角，避免过大的应力集中。

应力集中引起的最大等效应力值在材料的弹性极限范围内，若在弹塑性范围内充分应用材料则可优化联接结构尺寸，或在此结构尺寸下传递更大的扭矩。实际上，这样的结构设计是因为考虑到悬臂搅拌轴对刚度的要求以及联接的拆卸因素。

4 结束语

对圆锥过盈配合及压入过程受力进行分析和计算，并通过ANSYS Workbench进行仿真，得到了结合面上压力分布情况，与理论计算基本吻合，也验证了压入过程的建模计算。提取了锥孔内侧沿轴向的等效应力值，说明此结构具有较大的安全裕度。但是，分析中并未综合考虑锥面联接受轴向力或弯矩等工况，这还有待今后进一步的研究。

［1］魏延刚.轴毂过盈联接的应力分析和接触边缘效应［J］.机械设计，2004，21（1）：36-39.

［2］袁荣娟.锥面联接零件设计计算［J］.机械设计，2003，20（2）：42-43.

［3］许定奇，孙荣文.过盈联接的设计、计算与拆装［M］.北京：中国计量出版社，1992.

［4］MüftüS.Efficiency considerations for the purely tapered interference fit（TIF）abutments used in dental implants［J］.Journal of Biomechanical Engineering，2004，126：393-401.

［5］马连湘，刘光启，王文中.化工设备图算手册［M］.北京：化学工业出版社，2003.

［6］滕启，项忠霞.锥形轴联结设计计算的研究［J］.机械设计与制造，2002（2）：63-64.