Stewart六自由度动感平台结构优化设计

赵洁修，胡德计

（天津职业技术师范大学 机械工程学院，天津 300222）

0 引言

Stewart并联机构由2个平台和可伸缩旋转的6根支杆组成，下平台固定，上平台与模拟驾驶舱相连接。平台在空间具有6个自由度，结构灵活，空间占用面积小，并且具有错误并行非累加的特点［1］，故其广泛地应用于机器人结构及许多大型的模拟器中。

目前，Stewart平台有实心平台和中间镂空平台两种结构。关于两种结构的研究，大多应用传统力学方法对其进行力学分析。但是，Stewart平台由于其空间上的灵活性［2］，对其进行动力学分析时，其空间几何方面的数据量很大，且分析出来的数据对实际应用的价值不大，因而，简便而又实际的力学分析很有研究价值。而采用有限元分析的创新点在于，使用有限元软件代替传统的力学分析方法，可以解决传统力学分析的数据量大难以计算等问题。而且，不同场合、不同参数的平台，只需改变模型的设置参数［3］，即可快速实现其力学仿真。

1 Stewart平台的优化设计流程

本文分析的Stewart机构面向驾驶模拟系统，因而根据用途，构建其力学模型并为后续计算选定边界条件。Stewart并联机构的6个可以自由伸缩的杆件由伺服电机驱动伺服液压缸进行伸缩旋转，相互配合，完成动平台的任意动作。杆件与2个平台以万向铰链铰接在一起，铰链空间上呈三角形布局。铰链的布局如图1所示，机构的结构示意图如图2所示。

对实心结构和中空结构进行分析可知，实心平台强度大且承载力强，但在某些特殊场合，其质量太大，无法满足载荷限制条件；中空结构刚度大且质量轻，在某些场合比实心结构更适合；如果强度达到使用要求，则可以减轻结构重量，降低成本。

图1 铰链空间布局图

根据实际使用要求，上、下平台均采用铸铁材料。平台的设计中一般考虑如下参数：承载质量；X，Y，Z三向的极限位移量以及绕各轴的极限旋转角度。机构中的油缸、连接铰链等为标准零部件，根据实际给定参数及本设计面对的大型车辆模拟实际工况，选择合适的型号；上、下平台是非标准件，其尺寸及参数依据实际需求进行设计，此处以某型模拟器的参数为参考，应用三维造型软件，设计出并联机构的三维立体效果图如图3所示。

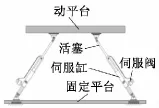
图2 机构的结构示意图

图3 并联机构的三维立体效果图

建好的三维模型，想要在有限元软件中进行数值分析，还需要进行结构简化和数据前处理，即网格划分和数字化处理［4］。

将模型导入分析软件后，需在软件中设置合理的边界条件，这里的边界条件可以根据实际应用场合进行更改。拟定分析流程如图4所示。

2 两种动平台结构的有限元分析

为了寻找最优化的平台结构，本文采用ANSYS软件对两种模型处于3个极限位置时的受力状态进行仿真，即：X和Y向300mm位置和转角15°位置［5］。3个极限位置上，杆件及平台受力最大，最容易出现断裂、过大的结构形变等失效。而除此以外的位置，受力及变形均小于此情况，因而，针对极限位置进行静力分析，找出两种结构的薄弱环节，即易失效点，可指导后续的结构优化。

3 结构优化分析结果及结论

在ANSYS软件中，通过设置边界条件和相关的参数进行仿真，可以得到平台结构在加载状态下的受力及变形情况，如图5～图8所示。

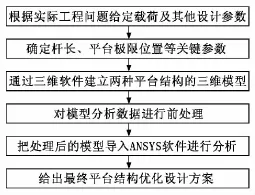
图4 拟定分析流程图

图5 实心平台极限位置变形图

图6 中空平台极限位置变形图

图7 实心平台极限位置应力图

图8 中空平台极限位置应力图

由图5～图8可见，最大的变形出现在上平台中部，此处容易出现过大变形引起的失效。但此处与模拟驾驶舱连接，模拟驾驶舱本身可以承受一部分变形，因而不需考虑其变形问题；可伸缩杆是整个结构中最薄弱的环节，容易出现应力过大导致的失效。整个结构的可靠性取决于支杆的可靠性［6］，如果支杆在极限位置不出现过大变形或者拉压失效，则整个结构可以认为是满足使用要求的。通过软件分析，最大形变量在材料允许的变形范围内；最大的应力集中在上平台与支杆的铰接点处，但最大应力仍未超出钢材的屈服极限，结构满足设计要求。

通过仿真，我们以表格的方式给出平台在极限位置的分析结果，表1为中空平台的分析结果，其最大的变形与应力出现的位置均不影响实际使用。采用中空结构平台可以满足实际的使用要求，达到预期的设计效果，因而，本例中的模拟器可以采用中空结构的上平台，既符合使用要求，又可以使整体质量减轻，达到节约成本的目的。

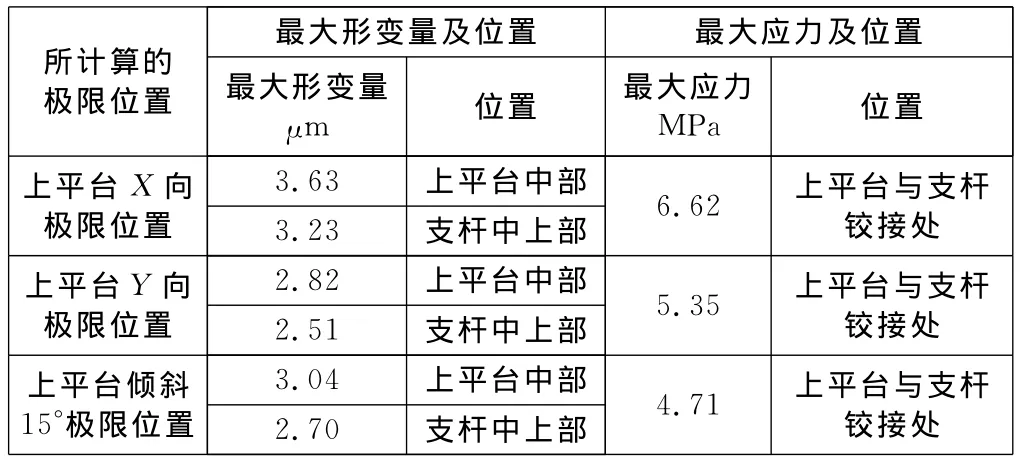
表1 中空平台三极限位置的最大应力、形变及发生位置

［1］Nguyen C C，Antrazi S S，Park J-Y，et al.Trajectory planning and control of a Stewart platform-based endeffector with passive compliance for part assembly［J］.Journal of Intelligent and Robotic Systems，1992，6：263-281.

［2］王勖成，邵敏.有限单元法基本原理和数值方法［M］.北京：清华大学出版社，1997.

［3］张波，盛和太.ANSYS有限元数值分析原理与工程应用［M］.北京：清华大学出版社，2005.

［4］杜平.Stewart平台运动学分析与仿真研究［J］.机械研究与应用，2012（4）：19-22.

［5］曹辉，严新平，吴超仲，等.基于动力学分析的驾驶模拟器运动仿真算法［J］.武汉理工大学学报，2005，29（3）：78-81.

［6］Peter R Grant，Lloyd D Reid.Motion washout filter tuning：rules and requirements［J］.Journal of Aircraft，1997，34（2）：145-151.