量子区分与量子克隆简述

曹怀信

（陕西师范大学 数学与信息科学学院，陕西 西安 710119）

量子信息是近二十年来迅速发展的信息学和量子力学相结合的一门交叉学科［1］.1982年，W.K.Wootters与W.H.Zurek合作在Nature上发表了题为“单量子不能被克隆”的论文［2］，证明了单量子无法被克隆.所以，量子密码原则上可以提供不可窃听、不可破译的保密通信系统.由于结合了量子力学的特性，信息学中的许多传统概念都得到了推广.例如，经典信息中，编码状态用0与1表示，信息是可以精确复制与区分的；而在量子信息中，由于量子态的叠加性使得非正交态不可区分、不可复制、也不可广播［3－5］等.文献［6-7］对量子克隆进行了全面的综述，并研究了恒等量子态的克隆问题.为了推广经典克隆，文献［8-9］引入了概率克隆的概念，发现幺正演化和选择性测量过程结合，确实能够以一定的概率产生从非正交集合中随机选出的输入态的精确复制.随着量子信息科学的迅猛发展，量子态的区分和克隆问题受到众多学者的关注［10－17］.

本文简要介绍量子态区分和克隆的数学概念及相关研究结果.值得指出的是，本文相关概念与结果是从文献中总结提炼出来，恕不一一指明出处.

1 量子态的区分

那么称算子组｛Mi为量子系统H上的一个量子测量（Quantum Measurement），且称M1，M2，…，Mn为测量算子.对任一｜φ〉∈S（H）（称为测量前系统的状态，即测量前的状态），记P｜φ〉（i）＝ 〈φ｜｜φ〉.如果P｜φ〉（i）＞0，那么称单位向量（状态）｜φi〉:＝Mi｜φ〉为用Mi测量后系统的状态，且称P｜φ〉（i）为事件“｜φ〉＝｜φi〉”发生的概率，即P｜φ〉（i）＝Prob｛｜φ〉＝｜φi〉｝，也称状态｜φi〉为测量的第i个结果.

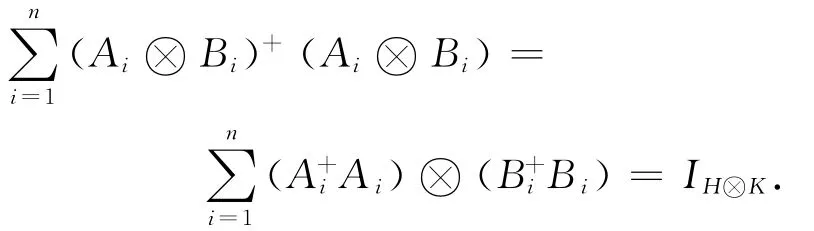
定义1 设S＝ ｛｜ψ1〉，｜ψ2〉，…，｜ψm〉｝是量子系统H中的一组状态（单位向量）.

（1）如 果 存 在 量 子 测 量M＝ ｛M1，M2，…，Mm＋1｝，使得m阶方阵（称为判定矩阵）C（S，M）∶＝［〈ψj｜｜ψi〉］为正定对角阵，那么称S是可区分的；否则，称S是不可区分的.

（2）如 果 存 在 量 子 测 量M＝ ｛M1，M2，…，Mm＋1｝，使得矩阵C（S，M）为单位阵，那么称S是可以可靠区分的；否则，称S不能可靠区分.

注1 设S＝ ｛｜ψ1〉，｜ψ2〉，…，｜ψm〉｝是可区分的，则存在量子测量M＝ ｛M1，M2，…，Mm＋1｝，使得矩阵C（S，M）∶＝［〈ψj｜M＋iMi｜ψj〉］为正定对角阵.于是，对任一｜ψ〉∈S，有〈ψ｜｜ψ〉≠0当且仅当｜ψ〉＝｜ψi〉.又因为〈ψi｜｜ψi〉＞0，所以，有以下判断:

（1）当〈ψ｜｜ψ〉＝0时，必有｜ψ〉≠｜ψi〉；

（2）当〈ψ｜｜ψ〉≠0时，｜ψ〉以概率pi＝ 〈ψ｜｜ψ〉取｜ψi〉，即P｛｜ψ〉＝｜ψi〉｝＝〈ψ｜｜ψ〉.这说明，可以概率pi＝〈ψ｜｜ψ〉肯定｜ψ〉＝｜ψi〉成立.

注2 设S＝ ｛｜ψ1〉，｜ψ2〉，…，｜ψm〉｝是可以可靠区分的，则存在量子测量M＝ ｛M1，M2，…，Mm＋1｝，使得矩阵C（S，M）为单位阵.于是，对任一｜ψ〉∈S，有〈ψ｜｜ψ〉＝1当且仅当｜ψ〉＝｜ψi〉.因而，有以下判断:

（1）当〈ψ｜｜ψ〉＝0时，有｜ψ〉≠｜ψi〉；

（2）当〈ψ｜｜ψ〉≠0时，｜ψ〉以概率pi＝ 〈ψ｜｜ψ〉＝1取｜ψi〉，即P｛｜ψ〉＝｜ψi〉｝＝1.这说明，能够以概率1（即可靠的）肯定｜ψ〉＝｜ψi〉成立.

定理1 （可靠区分准则）设S＝｛｜ψ1〉，｜ψ2〉，…，｜ψm〉｝是量子系统H中的一组状态，则S是可以可靠区分的当且仅当S是正交的.

必要性.设S是可以可靠区分的，则由定义1（2）知，存在量子测量M＝ ｛M1，M2，…，Mm＋1｝，使得矩阵C（S，M）为单位阵，即〈ψi｜｜ψi〉＝1，〈ψj｜｜ψj〉＝0（i≠j）.可见 ‖Mi｜ψj〉‖2＝〈ψj｜｜ψj〉＝0（j≠i）.

假设S＝ ｛｜ψ1〉，｜ψ2〉，…，｜ψm〉｝是非正交的，则 ∃i∈Δm＝ ｛1，2，…，m｝，使得｜ψi〉∉Vi＝｛｜ψj〉∶j∈Δm＼｛i｝｝⊥.由于H＝⊕Vi，所以存在常数kj（j∈Δm＼｛i｝｝）及｜φi〉∈Vi，使得

于是，

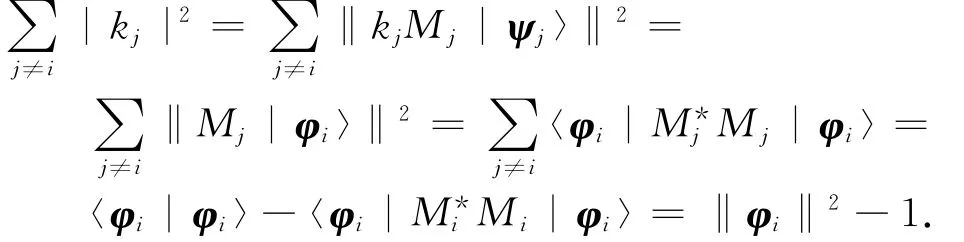
所以，‖φi‖≤1，矛盾.因此S是正交的.

定理2 （可区分准则）设S＝ ｛｜ψ1〉，｜ψ2〉，…，｜ψm〉｝是量子系统H中的一组态，则S是可以区分的当且仅当它是线性无关的.

证明 充分性.设S是线性无关的.令Vi＝｛｜ψj〉∶j∈ Δm＼｛i｝｝⊥.若Vi＼｛｜ψi〉｝⊥＝ Ø，则Vi⊂ ｛｜ψi〉｝⊥，从而｜ψi〉∈＝span｛｜ψj〉∶j∈Δm＼｛i｝｝，所以，｜ψ1〉，｜ψ2〉，…，｜ψm〉线性相关，矛盾.因此，∀i∈Δm，有

于是，存在非0向量｜vi〉∈Vi＼｛｜ψi〉｝⊥ （i＝1，2，…，m）.令｜ei〉＝ 〈vi｜vi〉－1/2｜vi〉，则〈ei｜ψi〉≠0，〈ei｜ψj〉＝0（i≠j）.令

则E＝｛E1，E2，…，Em＋1｝是量子测量，且C（S，E）为正定对角阵.所以，由定义1（1）知，S是可区分的.

必要性.设S是可区分的，则由定义1（1）知，存在量 子 测 量M＝ ｛M1，M2，…，Mm＋1｝，使 得 矩 阵C（S，M）为正定对角阵，即〈ψi｜｜ψi〉＞0，〈ψj｜｜ψj〉＝0（i≠j）.假设S是线性相关的，则存在i∈ Δm，使得｜从而，＝0.这与 ‖Mi｜ψi〉‖2＝〈ψi｜｜ψi〉＞0矛盾.故S是线性无关的.

推论1 设S＝ ｛｜ψ1〉，｜ψ2〉，…，｜ψm〉｝是量子系统H中的一组非正交态，则不存在量子测量M＝ ｛M1，M2，…，Mk｝及满射f:Δk→Δm使得正算子

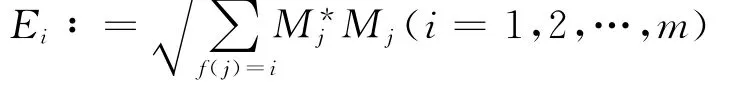
构成一个量子测量E＝ ｛E1，E2，…，Em，0｝，且C（S，E）为单位阵.

证明 假设存在这样的量子测量M及满射f，使得E＝ ｛E1，E2，…，Em，0｝是一个量子 测 量 且C（S，E）为单位阵.从而，S＝ ｛｜ψ1〉，｜ψ2〉，…，｜ψm〉｝是可以可靠区分的.这与定理1的结论相矛盾.

定义2 如果存在H上的正可逆线性算子T使得TS∶＝ ｛T｜ψ1〉，T｜ψ2〉，…，T｜ψm〉｝是可以可靠区分的，那么称S＝ ｛｜ψ1〉，｜ψ2〉，…，｜ψm〉｝是可以广义可区分的.

定理3 （广义可区分准则）设dimH＝n＜∞，则S＝ ｛｜ψ1〉，｜ψ2〉，…，｜ψm〉｝是可以广义可区分的当且仅当它是可以区分的.

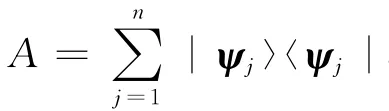
所以〈ψj｜A－1｜ψi〉＝δij.因此｛A－1/2｜ψk〉:k＝1，2，…，n｝为H的正规正交基.记T＝A－1/2，则TS∶＝｛T｜ψ1〉，T｜ψ2〉，…，T｜ψm〉｝为H中的正规正交系，因而是可以可靠区分的（定理1）.再由定义2知S是广义可区分的.

必要性.设S是广义可区分的，则存在H上的正可逆线性算子T使得TS∶＝ ｛T｜ψ1〉，T｜ψ2〉，…，T｜ψm〉｝是可以可靠区分的，从而为H中的正规正交系（定理1）.因此，｛T｜ψ1〉，T｜ψ2〉，…，T｜ψm〉｝是线性无关系.由于算子T是可逆线性，因此S也是线性无关的.故由定理2知，S是可以区分的.证毕.

推论2 设dimH＝n＜ ∞ 且S＝ ｛｜ψ1〉，｜ψ2〉，…，｜ψm〉｝是量子系统H中的一组线性无关态，则存在H上的新内积（··，），使得S为Hilbert空间（H，（··，））中的正规正交系，从而可以可靠区分.

证明 由定理3知，存在H上的正可逆线性算子T使得TS∶＝｛T｜ψ1〉，T｜ψ2〉，…，T｜ψm〉｝是可以可靠区分的.从而，由定理1知，TS成为H中的正规正交系.定义（｜x〉，｜y〉）＝ 〈x｜T＋T｜y〉＝〈x｜T2｜y〉，则 得 到H上 的 新 内 积 （··，） 且（｜ψi〉，｜ψj〉）＝ 〈ψi｜T＋T｜ψj〉＝δij.

由此可见，S为 Hilbert空间（H，（··，））中的一组正交态.从而，由定理1可知，S关于新内积是可以可靠区分的.证毕.

2 量子态的克隆

量子克隆问题（QCP）:是否存在一个状态｜0〉∈S（H）及酉算子U∈B（H⊗H）使得∀｜φ〉∈S（H），有U（｜φ〉｜0〉）＝｜φ〉｜φ〉？当U（｜φ〉｜0〉）＝｜φ〉｜φ〉成立时，称状态｜φ〉被U确定克隆（复制）了.所以，QCP等价于:是否存在一个量子装置（即酉算子）可以确定地克隆任意一个状态？

显然，单个状态必然是可以确定克隆的.

定理4 （不可线性克隆定理）当dim（H）≥2时，对任一状态｜0〉∈S（H）及H⊗H上的任一线性算子T，都存在状态｜φ〉∈S（H）使得T（｜φ〉｜0〉）≠｜φ〉｜φ〉.等价地说，命题“存在｜0〉∈S（H）及线性算子T使得对任意的｜φ〉∈S（H），都有T（｜φ〉｜0〉）＝｜φ〉｜φ〉”是错误的.

证明 假定存在｜0〉∈S（H）及线性算子T使得对任意的｜φ〉∈S（H），都有T（｜φ〉｜0〉）＝｜φ〉｜φ〉.因为dim（H）≥2，所以存在｜φi〉∈S（H）（i＝1，2）使得｜φ1〉⊥｜φ2〉.令a＝b＝/2，则a｜φ1〉＋b｜φ2〉∈S（H）.因为T（｜φ1〉｜0〉）＝｜φ1〉｜φ1〉，T（｜φ2〉｜0〉）＝｜φ2〉｜φ2〉，T（a｜φ1〉＋b｜φ2〉）｜0〉＝ （a｜φ1〉＋b｜φ2〉）⊗ （a｜φ1〉＋b｜φ2〉），且T是线性的，所以

于是，

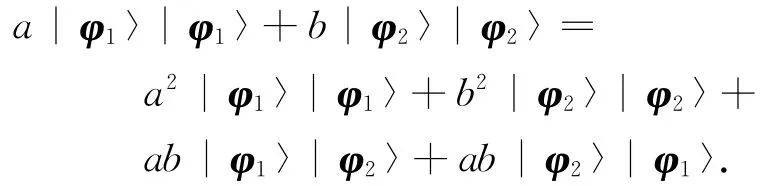
计算｜φ1〉｜φ1〉与上式两边的内积可得a＝a2.这与a＝b＝矛盾.证毕.

推论3 当空间H的维数大于或等于2时，对任一状态｜0〉∈S（H）及任一酉算子U∈B（H⊗H），都存在｜φ〉∈S（H）使得

定义3 设C（H）⊂S（H）.若存在｜0〉∈S（H）及酉算子U∈B（H⊗H），使得

则称C（H）是可以确定克隆的，此时，称酉算子U为量子克隆机，也称U可以确定克隆状态集C（H）.否则，称C（H）是不可确定克隆的.特别地，如果单态集C（H）＝｛｜φ〉｝是可以确定克隆的，那么称状态｜φ〉是可以确定克隆的.

由定义3及推论3可知，当dim（H）≥2时，全体量子态之集S（H）是不可确定克隆的，等价地说，不存在一个量子装置（即酉算子）可以确定地克隆任意一个量子态.下面的定理给出了一组量子态可以确定克隆的充分必要条件，可称为确定克隆准则.

定理5 （确定克隆准则）设1≤dim（H）＝d＜∞，则非空集C（H）⊂S（H）是可以确定克隆的当且仅当它是正交系.

证明 必要性.设C（H）是可以确定克隆的，则由定义3知，存在状态｜0〉∈S（H）及酉算子U∈B（H⊗H）使得（＊）式成立.假设C（H）不是正交系，则存在不同的两个态｜φ1〉，｜φ2〉∈C（H），使得〈φ1｜φ2〉≠0.因为U（｜φ1〉｜0〉）＝｜φ1〉｜φ1〉，U（｜φ2〉｜0〉）＝｜φ2〉｜φ2〉且算子U保持内积，所以〈φ1｜φ2〉＝ 〈φ1｜φ2〉2.因此，〈φ1｜φ2〉＝1.进而可知，存在常数c使得｜φ1〉＝c｜φ2〉.因为〈φ1｜φ2〉＝〈φ1｜φ2〉2，所以c＝1，即｜φ1〉＝｜φ2〉.这与｜φ1〉≠｜φ2〉矛盾.这就证明C（H）是正交系.

充分性.设C（H）是正交系，则它必为有限集.记C（H）＝ ｛｜ψi〉:i∈I｝，其中｜ψi〉≠｜ψj〉（i≠j）.任取｜0〉∈S（H）.显然，｛｜ψi〉｜0〉:i∈I｝与｛｜ψi〉｜ψi〉:i∈I｝都是有限维 Hilbert空间H⊗H中的正交系，且个数相同.将它们生成的线性子空间分别记为M、N.取M⊥、N⊥的正规正交基｛｜ej〉｝j∈J，｛｜εj〉｝j∈J，得到H⊗H的正规正交基:｛｜ψi〉｜0〉:i∈I｝∪ ｛ej｝j∈J与｛｜ψi〉｜ψi〉:i∈I｝∪ ｛εj｝j∈J.定义U｜ψi〉｜0〉＝｜ψi〉｜ψi〉（∀i∈I），U｜ej〉＝｜εj〉（∀j∈J），则得到酉算子U:H⊗H→H⊗H，满足U｜ψi〉｜0〉＝｜ψi〉｜ψi〉（∀i＝I），即（＊）式成立.所以，由定义3可知，C（H）是可以确定克隆的.证毕.

推论4 （不可克隆定理）不存在｜0〉∈S（H）及酉算子U∈B（H⊗H），使得

证明 由于全体量子态之集S（H）不是正交集，所以由定理5知S（H）是不可确定克隆的.

［1］Nielsen M A，Chuang I L.Quantum computation and quantum information［M］.London:Cambridge University Press，2000.

［2］Wootters W K，Zurek W H.A single quantum cannot be cloned［J］.Nature，1982，299:802-803.

［3］Barnum H，Caves C M，Christopher A F.Noncommuting mixed states cannot be broadcast［J］.Physical Review Letters，1996，76（15）:2818-2821.

［4］Piani M，Horodecki P，Horodecki R.No-local-broadcasting theorem for multipartite quantum correlations［J］.Physical Review Letters，2008，100:090502.

［5］Luo Shunlong，Li Nan，Cao Xuelian.Relation between“no broadcasting”for noncommuting states and“no local broadcasting”for quantum correlations［J］.Physical Review A，2009，79:054305.

［6］Fan Heng，Wang Yinan，Jing Li，et al.Quantum cloning machines and the applications［EB/OL］.［2014-09-15］.http:∥arXiv.org/pdf/1301.2956v4.

［7］Fan Heng，Liu Baoying，Shi Kangjie.Quantum cloning of identical mixed qubits［J］.Quantum Information ＆Computation，2007，7:551-558.

［8］Duan Luming，Guo Guangcan.Probabilistic cloning and identification of linearly independent quantum states［J］.Physical Review Letters，1998，80（2）:4999-5002.

［9］Duan Luming，Guo Guangcan.A probabilistic cloning machine for replicating two non orthogonal states［J］.Physics Letters A，1998，243（5）:261-264.

［10］Pati A K，Braunstein S L.Impossibility of deleting an unknown quantum state［J］.Nature，2000，404:164-165.

［11］Qiu Daowen.Some general probabilistic quantum cloning and deleting machines［J］.Physics Letters A，2003，308（5）:335-342.

［12］Martini F D，Pelliccia D，Sciarrino F.Contextual，optimal，and universal realization of the quantum cloning machine and of the NOT gate［J］.Physical Review Letters，2004，92:067901.

［13］Valerio S，Sofyan I，Nicolas G，et al.Quantum cloning［J］.Reviews of Modern Physics，2005，77:1225-1256.

［14］Van Enk S J.Relations between cloning and the universal NOT derived from conservation laws［J］.Physical Review Letters，2005，95:010502.

［15］Dang Guifang，Fan Heng.General sequential quantum cloning［J］.Journal of Physics A:Mathematical and Theoretical，2008，41:155303.

［16］Zhang Wenhai，Yu Longbao，Yang Ming，et al.Quantum cloning with multicopy ind-dimensions［J］.Science China:Physics， Mechanics and Astronomy，2011，54（12）:2217-2224.

［17］Shen Yao，Hao Liang，Long Guilu.Why can we copy classical information［J］.Chinese Physics Letters，2011，28（1）:010306.