基于变换的线性约束斜投影波束形成算法

汤 辰， 徐 亮， 毕传兴

（合肥工业大学 机械与汽车工程学院，安徽 合肥 230009）

自适应波束形成技术是阵列信号处理的重要组成内容，它通过对传声器阵列输出进行空域滤波，来达到增强有用信号、抑制干扰的目的［1－2］。线性约束最小方差（linearly constrained minimum variance，简称 LCMV）算法［3－5］是自适应波束形成的主要算法之一，它在保证对期望信号方向增益为一定值的条件下，计算最优权向量使阵列输出功率最小。在线性约束条件中，零点约束可以用来抑制非平稳干扰［6－7］，广义的基于特征空间的波 束 形成器 （generalized eigenspace－based beamformer，简称GEIB）把线性约束和特征空间技术结合起来运用到波束形成中［8］，该波束形成器将LCMV算法的权向量向修正的信号子空间投影，使权向量的范数变小，具有较快的收敛速度和较强的稳健性。但该波束形成器需要计算修正的信号子空间，因而容易产生计算上的不稳定，并且在零点约束方向与干扰方向接近时性能急剧下降。基于变换的线性约束特征干扰相消器和基于变换的线性约束正交投影算法［9］可以解决在特定干扰角度上数值稳定性下降和约束零点损失问题，但它们只适用于阵列数据不含期望信号（如自适应雷达）时的情况。基于变换的广义特征空间波束形成器（transformation－based GEIB，简称T－GEIB）［10］可在保留与GEIB相同的零点约束情况下，不需要计算修正的信号子空间，因此具有较高的数值稳定性。然而，该波束形成器是以GEIB为基础的，由于GEIB完全舍弃噪声子空间，只保留了信号子空间的分量，因此当期望信号相对干扰信号较大时，该方法非常有效；当期望信号相对干扰信号较小时，直接舍弃权向量在噪声子空间的分量会产生较大的误差，此时得到的权值不是最优权值，它将导致输出的信干噪比下降，波束畸变，从而造成抗干扰能力的下降。

以上算法都要求期望信号与干扰信号是不相干的，而在实际环境中，由于多径传播现象的影响，相干信号是普遍存在的，因此探索一种既适用于不相干又适用于相干环境下的信号目标方位估计算法很重要。本文将斜投影方法运用到自适应波束形成中，提出一种基于变换的线性约束斜投影波束 形 成（transformation－based linearly constrained oblique projection beamforming，简称TLCOBPB）算法，该算法首先采用变换矩阵对接收信号进行变换，然后将LCMV算法的静态权向量向信号子空间作斜投影得到自适应权向量，从而实现自适应波束形成。为验证本文方法的有效性和优越性，在低信噪比、低快拍数和相干信源情况下对该方法的波束形成性能进行数值仿真研究，并与现有的LCMV算法和T－GEIB进行比较。

1 阵列信号模型

考虑一M元均匀线阵列，有J＋1个窄带信号入射，包括1个期望信号和J个干扰信号，则阵列接收信号可表示为：

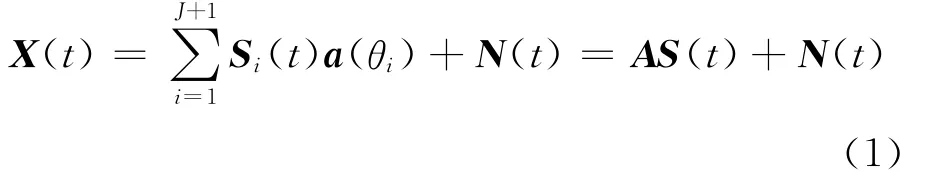
其中，Si（t）为信号的复包络；a（θi）为信号的导向矢量；N（t）为背景噪声，假设它为空间白噪声且与信号不相关；A为方向矩阵；S（t）为信源向量。设i＝1时为期望信号，i＝2，…，J＋1时为干扰信号，则方向矩阵A＝［a（θ1），a（θ2），…，a（θJ＋1）］，信源向量S（t）＝［S1（t），S2（t），…，SJ＋1（t）］T。

接收信号的协方差矩阵表示为：

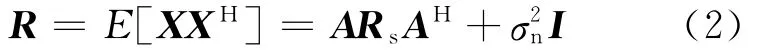
其中，E［］表示期望，上标H表示共轭转置；Rs为信号复包络的协方差矩阵为噪声功率；I为单位阵。假设信号源数目J＋1＜M，对R进行特征分解可得：

其中，λ1≥λ2≥…≥λJ＋1≥λJ＋2＝…＝λM＝为相应的M个特征值，其对应的特征矢量分别为ei，i＝1，2，…，M。

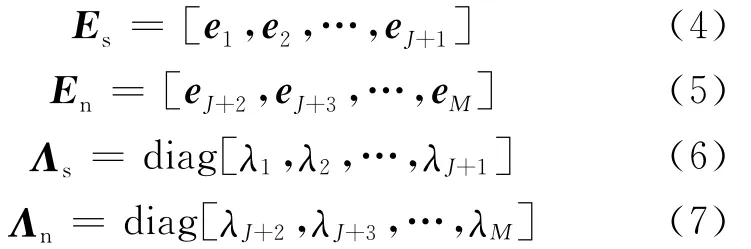
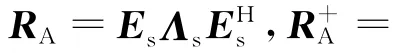
2 T－GEIB

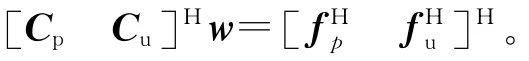
由以上的线性约束可得LCMV算法的自适应权向量为：

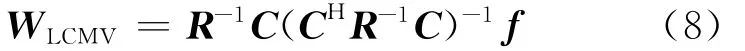
因为保留的线性约束为固定零点约束，所以需保留的线性约束可表示为

T－GEIB结构如图1所示。

图1中，变换矩阵T为Cp的正交补，（t）＝THX（t）LCMV对变换后数据的最小方差波束形成器可表示为如下最小化问题：

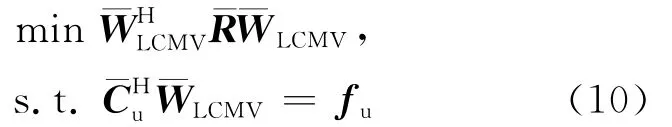
（10）式的解为：

某型号为N300-16.7/537/537-8的300 MW机组于2006年3月投产。机组有3个临界转速，分别为1370 r/min、1688 r/min、1750 r/min。该机组于2017年9月大修时配套进行节能升级改造，更换了高中压缸隔板汽封、高中压缸前后汽封、高中压缸过桥汽封，所有汽封间隙全部按技术规范下限调整。

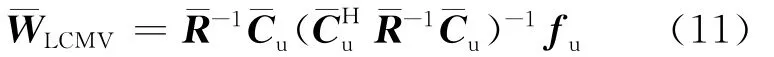
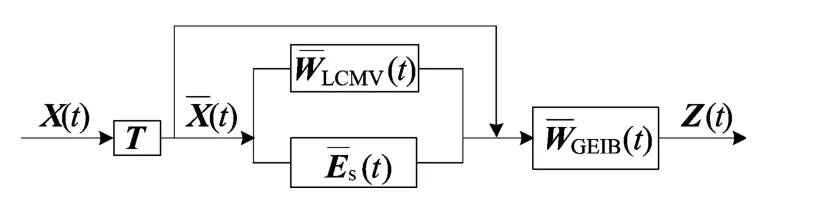
图1 T－GEIB结构图

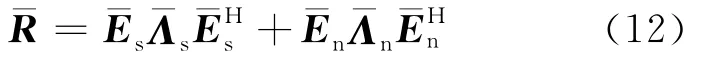
其中，的列向量张成的信号子空间，的列向量张成的噪声子空间，将LCMV向变换域的信号子空间作投影可得：

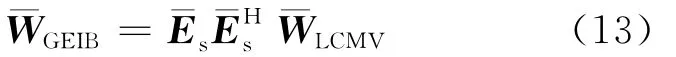
则T－GEIB的自适应权向量为：

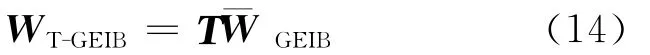
由（14）式可知，T－GEIB的自适应权向量位于Cp的正交补空间内，从而T－GEIB的自适应权向量满足（9）式的零响应约束，与GEIB方法相比，TGEIB不需要计算修正的子空间，即不需进行Gram－Schmidt正交化过程，因此具有更好的数值稳定性，并且计算量也大大减少。

3 T－LCOBPB算法

T－GEIB虽然摒弃了GEIB计算上的缺点，减小了计算量并使得数值稳定性上升，但该波束形成器是基于GEIB发展起来的，因此它从原理上保留了GEIB的缺点。首先，GEIB要求期望和干扰信号是不相关的，当期望和干扰是相干信号时，不能区分2种信号；其次，该波束形成器在期望信号相对干扰信号较大时非常有效，当期望信号相对干扰信号较小时，由其得到的权值将导致输出的信干噪比性能下降，波束畸变，抗干扰的能力下降。本文针对T－GEIB波束形成原理上的不足，在自适应波束形成中引入斜投影方法，进而提出T－LCOBPB算法，斜投影可有效消除相干干扰，从而提高波束形成的鲁棒性。

3.1 斜投影基础原理

正交投影通常运用到声源估计和定位中，而斜投影是另一种投影方法。在阵列信号处理中，斜投影算子用来将某个值（如测量声压）沿着与任意一子空间的斜向方向投影到一个低秩子空间，落在该低秩子空间里的成分被认为是研究者感兴趣的信号，子空间之外的被认为是干扰或者噪声，通过这种方式能有效去除干扰信号，并使干扰产生零陷，从而增强输出期望信号［13－15］。

设矩阵H∈Cn×m（n≥m），它的投影算子为PH（共轭、对称），与其正交的空间〈A〉＝〈H〉⊥，则PH＝H（HHH）－1HH，PA＝I－PH；它的斜投影算子为EHS（幂等、非对称），其零空间为〈S〉，则

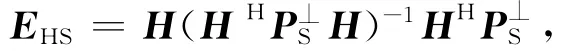
其中，为空间〈S〉的零导向算子，它有以下性质：EHSH＝H，EHSS＝0。

若定义B＝［H，S］，则

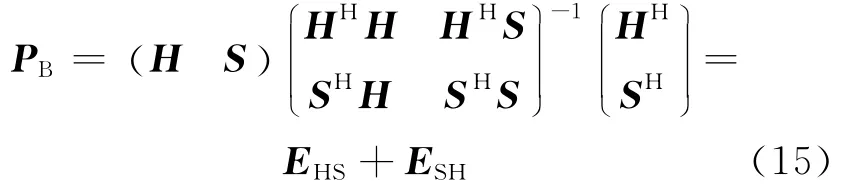
由（15）式可知矩阵B的投影矩阵PB可表示为2个斜投影矩阵之和。

3.2 T－LCOBPB算法

本文提出的LCOBPB算法将LCMV算法的静态权向量C（CH）－1f（对应线性约束）向信号子空间作斜投影得到自适应权向量，其权向量为

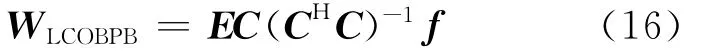
根据斜投影算子定义，可得

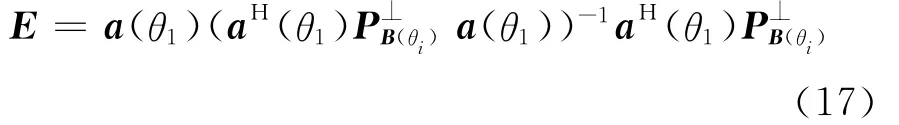
其中，B（θi）＝［a（θ2），…，a（θJ＋1）］为干扰信号的方向矩阵。（17）式表明斜投影算子需要知道期望信号和所有干扰信号的方向矢量，这在实际中很难满足。由文献［16］可知，斜投影矩阵也可以表示为：

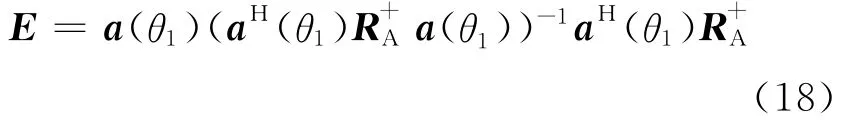
为了保留原有的固定零点线性约束，需要在自适应算法之前先进行固定零点的阻塞，TLCOBPB算法流程如图2所示。

图2 T－LCOBPB算法流程图

图2中，变换矩阵T为Cp的正交补，（t）＝THX（t），LCOBPB算法对变换后数据的权向量为：

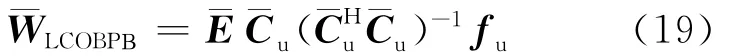
其中

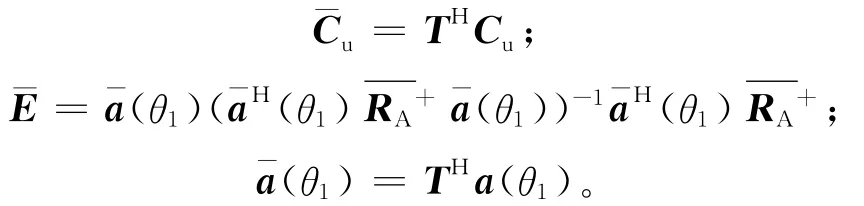
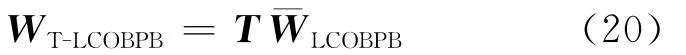
4 数值仿真与性能分析

为验证提出的T－LCOBPB算法在低信噪比、低快拍数和相干信源下的有效性和优越性，下面通过在几种不同情况下的数值仿真对其进行性能分析，每一个仿真结果都由100次独立实验结果平均得到。试验中采用12元的均匀线阵列，阵元间隔为半波长。

（1）在低信噪比下的干扰抑制能力。仿真中采用了2个信源，其中期望信号的方向为0°，1个与期望信号不相干的窄带干扰信号来自－30°，干噪比为20dB，有1个零点约束，其约束方向为50°，快拍数为500，分别给出了 SNR 为5、－20dB情况下的波束形成方向图，如图3、图4所示。

从图3中可以看出，在SNR＝5dB情况下，LCMV算法虽然能正确指向期望信号方向，但旁瓣较高；T－LCOBPB算法和T－GEIB的波束形成性能相当，它们主瓣都对准了期望信号的方向，但T－GEIB在干扰方向的增益略大于T－LCOBPB算法。

从图4中可以看出，在SNR＝－20dB情况下，T－GEIB在期望信号方向处的主瓣有所偏移，而且抗干扰性能严重恶化；LCMV算法波束形成性能较好，但其旁瓣还是略高于T－LCOBPB算法；T－LCOBPB算法效果很稳定，与SNR＝5dB时的波束形成性能几乎一致，表明在低信噪比情况下，T－LCOBPB算法有着比T－GEIB更好的干扰抑制能力。

（2）在低快拍数条件下的性能研究。取快拍数为5，SNR＝5dB，其他仿真条件同上，3种算法的波束形成方向图如图5所示。从图5可以看出，LCMV算法在期望信号点处产生零陷，不能达到增强期望信号的目的；T－GEIB和T－LCOBPB算法在固定零点处都产生了零陷，但TLCOBPB算法的波束形成性能要好于T－GEIB，它在干扰方向的增益小于后者，而且旁瓣水平相比于T－GEIB较低，表明在低快拍数条件下，TLCOBPB算法有着更好的干扰抑制能力。

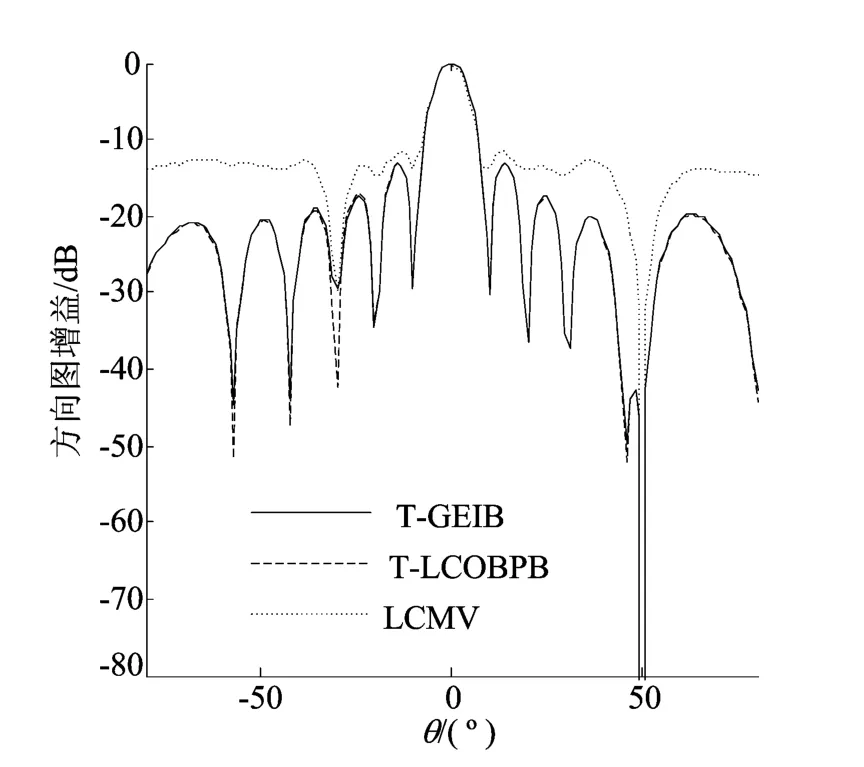
图3 SNR＝5dB时3种算法的方向图比较

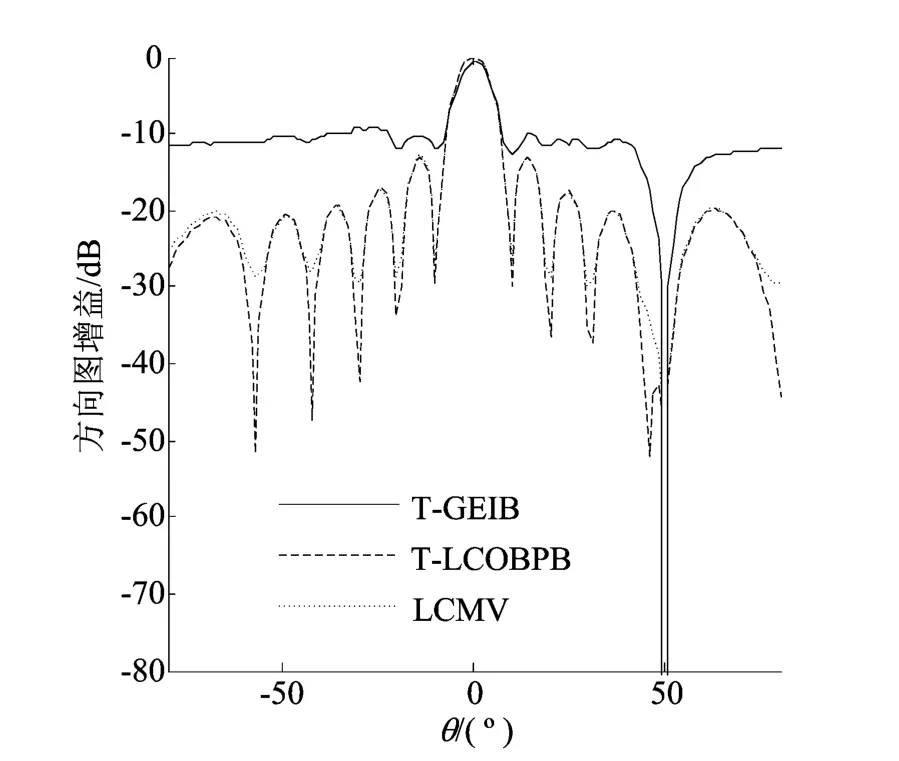
图4 SNR＝－20dB时3种算法的方向图比较

图5 快拍数为5时3种算法的方向图比较

（3）在相干信源条件下的波束形成性能研究。仿真中，期望信号与干扰信号相干，SNR＝10dB，快拍数为500，其他仿真条件同上，3种算法的波束形成方向图如图6所示。从图6可以看出，在期望信号与干扰信号相干情况下，LCMV算法和T－GEIB都产生了1个主瓣和1个栅瓣，不能区分期望信号和干扰信号，且旁瓣水平高于T－LCOBPB算法；而 T－LCOBPB算法有着较好的波束形成性能，既成功地去除了相干干扰声源的影响，又有着较低的旁瓣水平。

（4）同时存在2个干扰信号和2个零点约束的情况。仿真中，期望信号来自0°，SNR＝10dB，2个与期望信号相干的窄带干扰信号分别来自－30°和－20°，干噪比都为20dB，有2个零点约束，其约束方向为50°和27°，快拍数为500，其波束形成方向图如图7所示。

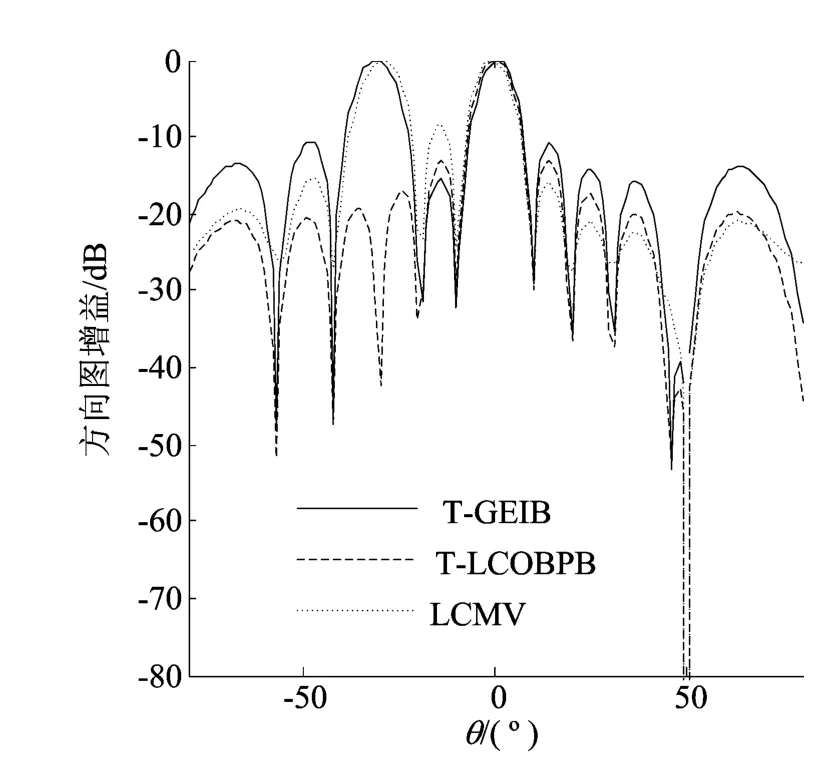
图6 信号相干情况下3种算法的方向图比较

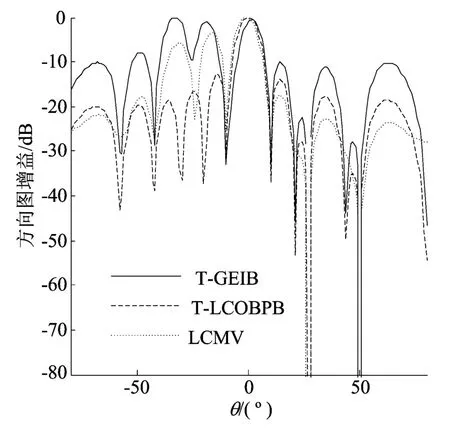
图7 干扰和固定零点不重合时的方向图比较

由图7可以看出，T－LCOBPB算法和 TGEIB在2个固定零点处都产生了零陷，T－GEIB在期望信号的主波瓣有所偏移，在干扰方向－30°和－20°处几乎形成了2个栅瓣，不能区分期望和干扰信号，且旁瓣水平也较高；T－LCOBPB算法成功地增强了期望信号，且在2个干扰方向处的增益很小，有着很好的相干干扰抑制能力。

（5）1个干扰信号与固定零点重合的情况。2个窄带干扰信号分别来自27°和－20°，其他仿真条件同上时，其生成的波束形成方向图如图8所示。从图8可以看出，T－GEIB和T－LCOBPB算法在2个固定零点处都产生了零陷，但TGEIB在期望信号的主波瓣还是有所偏移，在干扰方向－20°处形成了栅瓣，不能区分期望信号和干扰信号，且其他旁瓣水平也高；T－LCOBPB算法的主波瓣准确地指向了期望信号的方向，且成功地抑制了干扰，有着较好的波束形成性能。

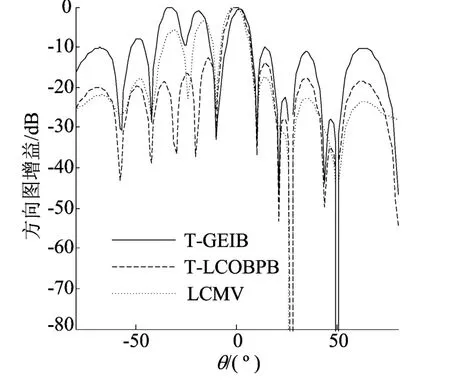
图8 干扰和1个固定零点重合时的方向图比较

5 结 论

本文针对T－GEIB在低快拍数、低信噪比和相干信源条件下波束形成性能下降这一问题，将斜投影运用到自适应波束形成中，提出T－LCOBPB算法，该算法用变换矩阵对接收信号进行变换后，将LCMV算法的静态权向量向信号子空间作斜投影得到自适应权向量，斜投影可有效消除干扰，进而提高波束形成的鲁棒性。仿真结果表明：T－LCOBPB算法在高、低信噪比条件下均能生成稳定的波束形成方向图，且在低快拍数和相干信源条件下也能生成较好的波束形成方向图；该算法有着比T－GEIB更好的干扰抑制能力。

［1］ Wei Zhe，Huang Jianguo，Hui Yuejiao.Adaptive beamforming based multiple targets signal separation［C］／／2011 IEEE International Conference on Signal Processing，Communications and Computing，Xi'an，2011：1－4.

［2］ Iozsa A.Adaptive beamforming applied for signals estimated with direction－of－arrival algorithms from the ESPRIT family［C］／／International Symposium on Electronics and Telecommunications，Timisoara，2012：397－400.

［3］ He Nan，He Yulin.Research and comparison of anti－jamming performances of LMS and LCMV algorithm based on MATLAB simulation［C］／／2011 10th International Conference on Electronic Measurement ＆Instruments，Vol 1，Chengdu，2011：98－101.

［4］ Peled Y.Linearly constrained minimum variance method for spherical microphone arrays in a coherent environment［C］／／Joint Workshop on Hands－free Speech Communication and Microphone Arrays，Edinburgh，2011：86－91.

［5］ Bertrand A.Distributed distortionless signal estimation in wireless acoustic sensor networks［C］／／Proceedings of the 20th European Signal Processing Conference，Bucharest，2012：1254－1258.

［6］ Er M H.Linear antenna array pattern synthesis with prescribed broad null［J］.IEEE Trans on Antennas and Propagation，1990，38（9）：1496－1498.

［7］ Lee G.Coordinated beamforming with relaxed zero forcing［C］／／International Conference on Wireless Communications and Signal Processing，Nanjing，2011：1－5.

［8］ Yu J L，Yeh C C.Generalized eigenspace based beamformers［J］.IEEE Trans on Signal Processing，1995，43（11）：2453－2461.

［9］ 丁前军，王永良，张永顺.基于变换的线性约束降秩自适应波束形成算法［J］.系统工程与电子技术，2005，27（12）：2010－2013.

［10］ Yu J L，Leou M L.Transformation－based adaptive array beamforming［J］.Signal Processing，2000，80 （2）：231－241.

［11］ Er M H，Cantoni A.A unified approach to the design of robust narrow－band antenna array processors［J］.IEEE Trans on Antennas and Propagation，1990，38（1）：17－23.

［12］ Applebaum S P，Chapman D J.Adaptive arrays with main beam constraints［J］.IEEE Trans on Antennas and Propagation，1976，24 （5）：650－662.

［13］ Behrens R T，Scharf L L.Signal processing applications of oblique projection operators［J］.IEEE Trans on Signal Processing，1994，42（6）：1413－1424.

［14］ Hou Huijun.A generalized oblique projection operator for interference suppression under colored noise［C］／／IEEE Radar Conference，Atlanta，GA，2012：0687－0692.

［15］ Hong Hong.A multi－domain collaborative filter for HFSWR based on oblique projection［C］／／IEEE Radar Conference，Atlanta，GA，2012：0907－0912.

［16］ McCloud M L，Scharf L L.A new subspace identification algorithm for high－resolution DOA estimation［J］.IEEE Trans on Antennas and Propagation，2002，50（10）：1382－1390.