快速边缘粒子滤波在无序量测问题中的应用*

袁 丁，胡建旺，吉 兵，顾 峰

（1.军械工程学院 信息工程系，河北 石家庄 050003;2.73903部队，福建 厦门 361000）

0 引言

在目标跟踪系统中，由于所用传感器具有不同的采样速率，以及传输中延迟的不同，测量同步很难被保证，从而产生了异步融合问题。更进一步，会出现来自同一目标的较早的量测在较晚的量测之后到达融合中心，即无序量测（out-of-sequence measurement，OOSM）现象［1］。传统的卡尔曼滤波（KF）算法不能直接处理这种“负时间量测更新”问题，需要研究相应的滤波算法。

目前，最适合对无序量测（OOSM）作实时处理的滤波思想是直接更新法。直接更新法是直接利用OOSM和已存储的目标状态充分估计量，对当前状态估计直接进行再更新，以得到新的状态估计及其估计误差协方差矩阵［2］。直接更新法存储量和计算量较小，且输出没有滞后，在这一滤波思想下，学者提出了诸如A1，B1，AA1，FPFD等线性系统下的最优或次优滤波算法。

对于弱非线性高斯系统，可以通过泰勒级数展开将非线性问题转化为线性，但在应用扩展卡尔曼滤波（EKF）时，线性化过程会导致较大的滤波误差［2］。文献［3］提出了基于无迹卡尔曼滤波（UKF）的OOSM算法，通过UT避免了求解非线性量测方程的雅可比矩阵或海塞矩阵。对于强非线性高斯系统，Ortan推导得到了加入OOSM后的后验密度，提出了OOSM 粒子滤波（OOSM-PF）算法［4］，此后又有学者提出了使用高斯粒子滤波（GPF）、Uscented粒子滤波（UPF）、有效性存储粒子滤波（SEPF）的 OOSM 滤波算法［5～7］。但以PF为基础的算法需要解决计算量和存储量大的问题。

对此，本文提出以快速边缘粒子滤波（fast marginalized PF，FMPF）为基础的新的非线性OOSM处理算法。通过结合FMPF算法与前向预测滤波思想，算法可有效处理一步或多步OOSM问题，且降低了计算复杂度与存储量，实时性更好。

1 问题描述

考虑非线性离散时间系统［2］

其中，xk为k时刻目标状态向量，fk，k-1（·）为离散时间非线性状态转移函数，wk，k-1为从时刻k-1到时刻k的累积过程噪声。zk为k时刻量测向量，hk（·）为非线性量测函数，vk为k时刻量测噪声。假设初始时刻，目标初始状态，过程噪声与量测噪声之间互不相关。

在时刻k，使用贝叶斯滤波方程可以得到后验分布p（xk|z1∶k），继而得到k时刻的目标状态估计值和误差协方差矩阵Pk|k。随后，来自较早时刻d的量测zd，在状态估计被计算出后到达融合中心。这里假定zd为l步滞后，即有tk-1＜td＜tk。其中，1≤l≤s，s为延迟量测到达融合中心的最大滞后时间。

需要解决的问题是:用延迟量测zd来更新后验分布p（xk|z1∶k），以便获得最后的后验分布 p（xk|z1∶k，zd），继而得到最新的状态估计。

2 FMPF

FMPF在处理时，将目标跟踪模型视为含有线性子结构的非线性状态空间模型。其中，位置信息是强非线性信息，而速度信息是线性信息。此时，系统方程式（1）、式（2）可分解为

由此，可以将滤波过程分为并行的两部分，采用PF处理非线性部分，采用KF处理线性部分。而FMPF其实是在MPF的基础上，对线性部分的处理作了简化，仅用一个KF对线性部分进行状态估计，进一步节约计算资源。FMPF处理流程如图1所示，具体实现过程可参见相关文献［8～11］。

3 算法设计

新算法采用前向预测方法来处理OOSM问题。作为直接更新法的一种，前向预测法在使用时需要解决2个问题，即如何构建包含延迟量测的重构航迹和如何实现重构航迹与已有航迹的融合。在FMPF框架下，算法将状态变量分成非线性与线性两部分，并分别采用不同方式解决上述问题，现介绍如下:

图1 FMPF处理流程图Fig 1 Flow chart of FMPF processing

1）非线性部分处理

在此，借鉴现有的OOSM—PF算法处理延迟量测。

假设根据量测时戳，可以找到延迟量测zd在量测序列z1∶k中的位置。此时，还需要td-1时刻的状态估计-1|d-1和估计误差协方差矩阵。算法具体步骤为:

a.初始化

在延迟量测zd到达融合中心以后，由p（）产生粒子群，粒子对应的权值为

b.利用延迟量测zd，完成更新

首先，各粒子一步预测为

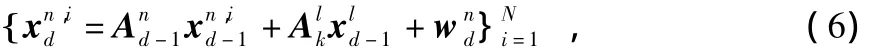
进而，更新粒子权值为

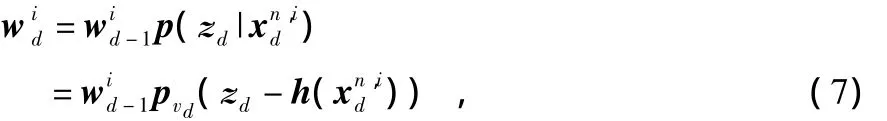
并归一化为

其中，i=1，2，…，N。

由此，可得到状态估计及其协方差矩阵为

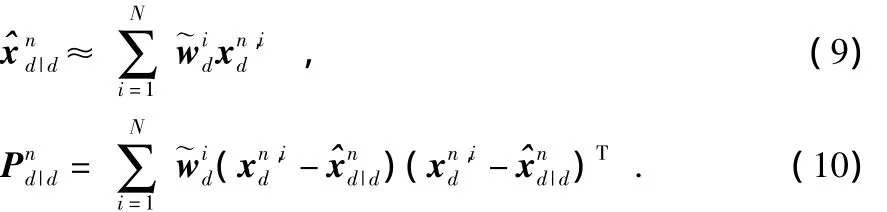
2）线性部分

a.完成由td-1→td的更新

由于td-1时刻的状态估计及其对应的误差协方差矩阵已知，此时有

b.完成由td→tk的更新

由td→tk的更新可参照式（11）～式（15）进行，在此不再赘述。由此，可以得到和，完成了重构航迹的构建。

c.融合重构估计与已有估计

由此，得到了基于OOSM-FMPF的处理算法。算法在FMPF框架下，结合前向预测滤波思想处理OOSM。在非线性部分，算法将已有估计作为量测值，再次进行滤波。在线性部分，则借鉴航迹融合方法，通过加权等融合算法实现再更新。与现有算法相比，新算法实时性更好，这主要是因为:

1）算法采用FMPF框架，减小了非线性状态向量的维数，使算法的计算复杂度降低。而FMPF与MPF相比，则进一步减小了线性部分的计算量。

2）新算法采用前向预测滤波，在非线性部分处理时，不需要存储大量的粒子及其权重;而对于线性部分，也不需要存储过去的量测或更新;从而减小了算法的存储量。

此外，在FMPF框架下，可以采用一些改进的更优算法，如采用OOSM-UPF或OOSM-GPF算法代替OOSM-PF处理非线性部分从而进一步提高算法性能。

4 仿真实验

仿真实验中，采用二维空间中的运动模型为

取状态变量为xk=［xkyk］T，其中，位置信息［xk，yk］T为强非线性信息，速度信息［］T为线性信息。目标运动航迹如图2所示。

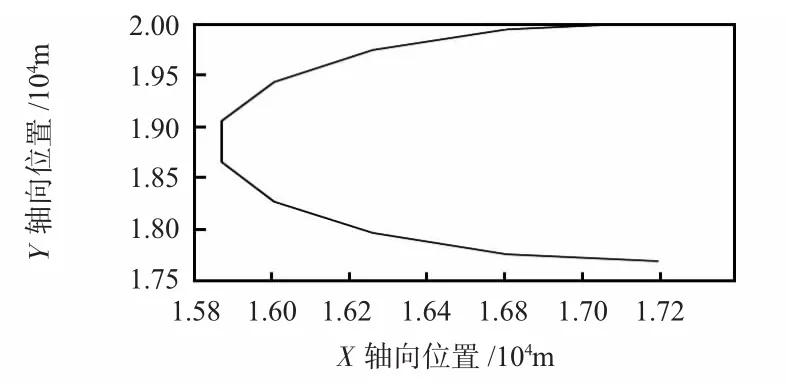
图2 目标运动轨迹Fig 2 Target trajectory

实际量测过程中得到的是目标的距离r和偏转角θ。量测方程为

将式（16）改写为式（3）～式（4）所表示的MPF模型结构。模型中各参数为

假设传感器获得10个量测，在传输过程中，延迟量测在最后一个采样间隔到达。仿真时，考虑单步延迟和两步延迟的情形。同时，分别采用正常时序处理、OOSM-FMPF算法以及丢弃滞后法等3种方式处理这组量测，以验证算法性能。进行50次Monte Carlo仿真，图3、图4给出了单步延迟情形下使用3种算法所得X轴向与Y轴向的估计，表1给出了单步延迟和两步延迟的情形下算法在X轴向估计的RMSE。

表1 不同延迟步数下X方向估计的RMSE（m）Tab 1 X-direction estimated RMSE with different delay step number

从表1和图2、图3的结果可以看出:本文提出的OOSM-FMPF在单步滞后与两步滞后的情形下，滤波精度都要高于丢弃滞后法，且接近正常时序处理结果，说明算法可以有效处理OOSM问题。

5 结论

本文针对非线性条件下的OOSM问题，提出了基于FMPF新处理算法。新算法保留FMPF算法框架，并采用前向预测方法处理OOSM。算法将状态变量分为线性和非线性两部分，分别采用相应的无序估计算法处理。新算法计算量与存储量更小，实时性更好。仿真实验也验证了算法性能。今后，可以考虑使用GPF等改进PF算法，代替本文算法中的标准粒子算法，进一步提高估计精度。

图3 一步延迟下X轴向估计Fig 3 X estimated with 1-step-lag

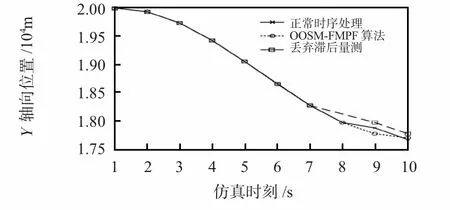
图4 一步延迟下Y轴向估计Fig 4 Y direction estimate with 1-step-lag

［1］韩崇昭，朱红艳，段战胜，等.多源信息融合［M］.2版.北京:清华大学出版社，2010:368-379.

［2］王 炜，黄心汉，王 敏.无序量测滤波更新算法综述［J］.控制与决策，2012，27（1）:1-5.

［3］陈金广，李 洁，高新波.基于UT变换的单步滞后无序量测算法［J］.中国科学:信息科学，2011，41（5）:638-648.

［4］Mahendra M，Kirubarajan T，Sanjeev A.Out-of-sequence measurement processing for tracking ground target using particle filters［C］//Proceedings of 2002 IEEE Aerospace Conference，2002:1809-1818.

［5］Wang W，Wang G B，Huang X H.et al.Gaussian particle filtering algorithm for out-of-sequence measurement problem［C］//Proceedings of 2011 International Conference on Electric Information and Control Engineering，2011:3297-3300.

［6］周建中，王树宗.一种基于粒子滤波的分布式跟踪算法［J］.武汉理工大学学报:交通科学与工程版，2010，34（5）:924-927.

［7］Karl B，Karl-Erik A，Anders R.Storage efficient particle filters with multiple out-of-sequence measurements［C］//Proceedings of 2012 15th International Conference on Information Fusion，Singapore，2012:471-478.

［8］朱志宇.粒子滤波算法及其应用［M］.北京:科学出版社，2010:132-134.

［9］薛 锋，刘 忠，石章松.快速Marginalized粒子滤波器在纯方位跟踪中的应用［J］.火力与指挥控制，2008，33（1）:66-72.

［10］陈金广，马丽丽，陈 亮.基于边缘粒子滤波的目标跟踪算法研究［J］.计算机工程与应用，2010，40（28）:128-131.

［11］邹卫军，陈 益，薄煜明.相似采样粒子滤波在混合系统估计中的应用［J］.电光与控制，2009，16（11）:55-59.