无线传感器网络煤矿井下RSSI自适应定位算法*
2014-12-31曹开来
曹开来,余 敏
(江西师范大学计算机信息工程学院,江西南昌 330022)
0 引言
煤炭是我国的主要能源,受我国煤矿复杂地形影响,矿难频发,煤矿安全已成为煤矿生产的重要环节。因此,实现煤矿井下人员实时有效的定位,不仅能够合理地调配资源,而且对发生矿难时的及时抢救,减少生命财产损失有着重要的意义。
目前,针对无线传感器网络煤矿井下的定位技术已有许多学者进行了研究,并取得一定进展。常用于煤矿井下的定位技术按照是否需要测距可分为无需测距(rangefree)算法与基于测距(range-based)算法 2种[1]。其中,Range-free定位算法的精度和收敛速度一定程度上依赖于网络节点密度,特别是当网络拓扑结构比较复杂时算法的性能将明显变差[2]。Range-based定位技术主要有:接收信号强度指示(received signal strength indication,RSSI),到达时间(time of arrival,TOA),到达时间差 (time difference of arrival,TDOA),到达角 (angle of arrival,AOA),其中 TOA,TDOA,AOA定位算法通常定位精度相对较高,但对节点的硬件成本要求也比较高,定位过程能量消耗较大,容易受到温度、湿度、障碍物等环境因素的影响[3,4]。RSSI定位算法由于目前大多数的节点都具有RF发射能力,不仅无需增加任何额外的硬件设备,而且成本低廉、能耗低,但是其测距精度容易受到煤矿井下复杂的巷道影响,导致其定位精度较低[5],因此,本文主要在传统无线传感网络RSSI定位算法的基础上进行改进,通过动态选择RSSI 测距模型中的路径损耗指数,提高节点测距精度,并结合煤矿井下巷道环境特征,提出一种适用于煤矿井下节点定位的自适应RSSI三角质心定位算法。
1 无线信号传播模型
自然界中,无线电信号随距离的增大有规律的衰减,无线信号传播模型就是利用这个原理测量两节点间距离的,无线信号传播理论模型主要有自由空间传播模型、对数距离路径损耗模型、对数—常态分布模型等,其中对数—常态分布模型的使用最为广泛。对数—常态分布模型[6]如式(1)

其中,PL(d)为距离发射点处d的接收信号强度,dB;d0为参考距离;PL(d0)为在参考距离d0的接收信号强度;n为路径衰减指数,通常是经过实际测量得到的经验值,取值的范围在2~5之间;Xσ为平均值为0的高斯分布随机变数,其标准差范围为4~10。在实际应用中,利用RSSI测距时,无线电传播路径衰减指数对于定位精度有很大的影响。
2 自适应RSSI定位算法
2.1 传统RSSI定位算法分析
煤矿井下巷道等环境多变,多路径效应明显,信号衰减快,而RSSI受环境影响较大,空气流动、温度变化、人员和设备的通过都将引起某点的信号强度变化[4],经实验测得在相同环境下不同的方向和区域RSSI值都会不同,如果不同区域采用固定的n值来计算盲节点到信标节点的距离将会产生较大的测距误差,如果能够动态获取盲节点区域的路径损耗指数将会极大提高RSSI的定位算法精度。
2.2 自适应RSSI三角质心定位算法
信标节点在部署时,在墙壁的同一侧安放,信标节点之间的距离为30m,信标节点的序号按从小到大的顺序排列,盲节点周围信标节点数≥3时,如图1所示。

图1 巷道结构图Fig 1 Structure diagram of roadway
1)当盲节点S需要定位时,首先广播一个需要定位的信号,假设信标节点Si(i=1,2,3,4,5)都可以收到盲节点的定位信号,这时信标Si(i=1,2,3,4,5)分别将它们的序号和到盲节点的RSSI值发送给盲节点。
2)当盲节点接收到多个信标节点的数据包后,提取RSSI值最大的前3个信标节点,并按RSSI值从大到小排列RSSI3>RSSI2>RSSI4,如图1所示,信标节点S4由于受到巷道壁的影响,信标节点S4到盲节点的RSSI值可能会小于信标节点S2到盲节点的值。此时盲节点将RSSI值最大的点S3作为中心信标节点,并将前3个节点序号链按RSSI值从大到小的顺序S3—S2—S4广播给周围的信标节点。
3)信标节点S1和S5接收到节点序号链后,若发现节点序号链中没有自己的节点序号,将进入休眠状态,盲节点到S3的RSSI值最大,表示S2和S4到S3的路径损耗指数n比较接近信标节点S2和S4到盲节点S的路径损耗指数,S2和S4到中心节点S3的距离已知,所以,可以通过式(1)计算其到中心信标节点S3的路径损耗指数分别为n2,n4,S3采用默认的路径损耗指数n。
4)信标节点S2,S3,S4将它们计算的路径损耗指数,重新发送给盲节点S,此时盲节点到3个节点的RSSI值分别为PL(di)[dB],(i=2,3,4),盲节点到 3 个信标节点的路径损耗指数分别为ni,(i=2,3,4),PL(d0)[dB]和d0通过测量获得,利用式(1)可以计算出盲节点到3个信标节点的距离分别为di,(i=2,3,4)。
5)此时可以获得 3 个圆的方程式(2),(X2,Y2),(X3,Y3),(X4,Y4)分别为信标节点S2,S3,S4的坐标,e2,e3,e4分别为它们的测量误差,运用三边定位法可以估算出盲节点的坐标(XS,YS)。但是巷道由于其狭长的特点,如果信标节点在同一条直线上时,传统三边定位法将无法适用,并且煤矿井下环境复杂,3个圆不一定会相交于一点,很多情况是一个区域[5],取这个区域的 3 个近似点M1,M2,M3,再以这3个近似点构成一个三角形,从而以三角形的质心为未知节点位置
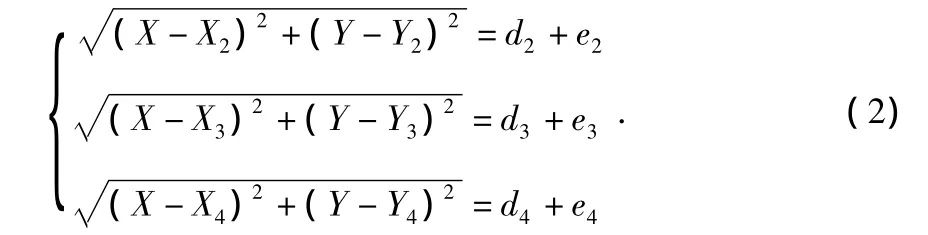
将两圆的位置情况分为两圆相交、两圆内切、两圆外切、两圆相离等4种情况,然后再根据直线巷道,向上弯道和向下弯道的情形进行讨论。
2.2.1 两圆相交
1)一个交点在巷道内,一个交点在巷道外
此时两圆相交有2个交点A,B,如图2所示,可以排除巷道外的点B,将位于巷道内的点A作为最后近似点M1。
2)2个交点都在巷道外
这种情况是因为测量的盲节点到信标节点距离超出了正常值导致。
a.对于直道情况,如图3(a)所示,交点A,B的连接线AB和信标节点S1,S2连线相交于点C(Cx,Cy),A,B相对于C点对称,取AC的中点作为为最后近似点M1。
b.对于弯道情况,如图3(b),(c)所示,取交点A,B的中点作为最后近似点M1,如果A,B的中点不在巷道内,则做巷道的中线与AB相交于M1点,M1作为最后的近似点。
假设巷道宽度为L,第三个信标节点S3和信标节点S1在同一条直线上,信标节点S1,S2,S3的坐标分别为(X1,Y1),(X2,Y2),(X3,Y3)则巷道中线L1的直线方程为


图2 一个交点在巷道内且一个交点在巷道外Fig 2 An intersection in the roadway,an intersection outside the roadway
巷道中线L2的直线方程为
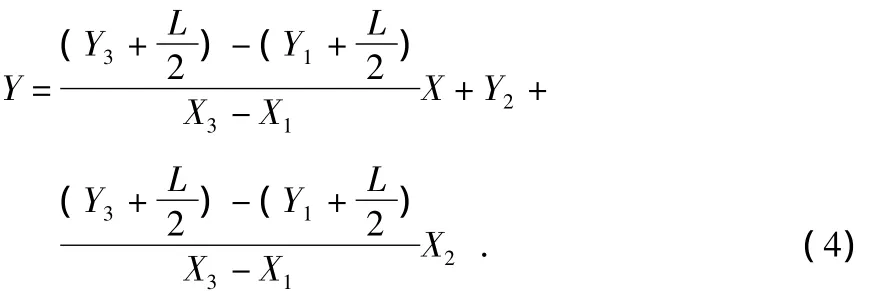


图3 两个交点都在巷道外Fig 3 Two intersections are outside the roadway
3)2个交点都在巷道内
a.对于直道情况,交点A,B一定是相对于巷道壁对称,所以,不会出现2个交点都在巷道内的情况。
b.对于弯道情况则将2个圆的相交点的坐标求平均,将均值定为未知节点的坐标。如图4所示,两圆的交点A,B连线的中点定为近似点M1。

图4 两个交点都在巷道内Fig 4 Two intersections are in the roadway
2.2.2 两圆外切
1)对于直道情况,两圆只有一个切点,则切点的坐标被定为作为最后的近似点M1,如图5(a)所示。
2)对于顺向弯道,如图5(b)所示,切点在信标节点S1与S2的连线上,而直线S1S2存在于巷道外,所以,切点会出现在巷道外的情况,说明测距存在较大误差,需要重新定位。
3)对于逆向弯道,如图5(c)所示,切点在信标节点S1与S2的连线上,而直线S1S2存在于巷道内,所以,切点不会出现在巷道外的情况,切点的坐标则被定为最后的近似点M1。

图5 两圆外切Fig 5 Two circles circumscribed
2.2.3 两圆内切
1)对于直道情况,两圆只有一个切点,则切点A的坐标则被定为作为最后的近似点M1,如图6(a)所示。
2)对于顺向弯道情况,切点在直线S1S2的延长线上,如图6(b)所示,切点A的坐标则被定为最后的近似点M1,若切点超出巷壁,说明存在测量误差,取巷壁中线与直线S1S2延长线的交点作为最后的近似点M1。
3)对于逆向弯道情况,切点在直线S1S2的延长线上,并在巷道外,说明存在测量误差,需要重新定位。
2.2.4 两圆相离
1)对于直道情况,如果2个圆与中轴线有4个交点,选取其中最内侧的2个交点A和B,将最内侧这2个交点的中心点定为未知节点的坐标,如图7(a),将两圆与巷道中线最内侧的2个交点:点A和点B的坐标求均值,则将A,B两点的中心点C定为最后的近似点M1。

图6 两圆内切Fig 6 Two circles is inscribed
2)对于顺向弯道和逆向弯道,两圆与中轴线有4个交点,同样取最内侧的2个交点A和B,2条巷道中线交点C,取A,B,C三点的质心作为为最后的近似点M1。
同理,可以得到其他两圆的近似点M2,M3。最后得到最后 3 个近似点M1(Xm1,Ym1),M2(Xm2,Ym2),M3(Xm3,Ym3),计算三角形的质心M(Xm,Ym)为未知节点的估测值。普通三角形质心为

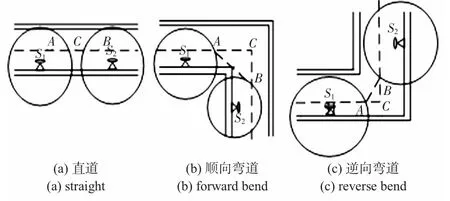
图7 两圆相离Fig 7 Deviation of two circles
3 仿真实验
本文采用Matlab模拟巷道环境,在1000m的狭长巷道内对自适应RSSI三角质心定位算法进行了定位仿真,并与传统的RSSI定位算法进行了比较,仿真实验将巷道宽度分为5,10,15 m的情况,并分别进行了500次仿真实验,信标节点在巷道壁同一侧安装,部署间隔为30 m。
由表1可以看出:采用改进的RSSI定位算法,在巷道宽度分别为15,10,5 m的情况下,误差平均值分别为0.46,0.45,0.39 m,比传统的RSSI定位算法精度有一定的改进,并且随着巷道宽度的减少,节点分布范围随之减少,定位误差也随之降低。由表2可以看出:改进后的RSSI定位算法在巷道宽度为15,10,5 m的情况下定位误差小于1 m的概率分别为91,92,95.7%,定位精度相比传统 RSSI定位算法有很大的提高。总之经过改进的自适应RSSI三角质心定位算法相比传统的RSSI定位算法在定位精度上得到了有效提高,能够较好地满足煤矿井下定位的要求。

表1 定位算法的点位误差比较Tab 1 Comparison of localization algorithm
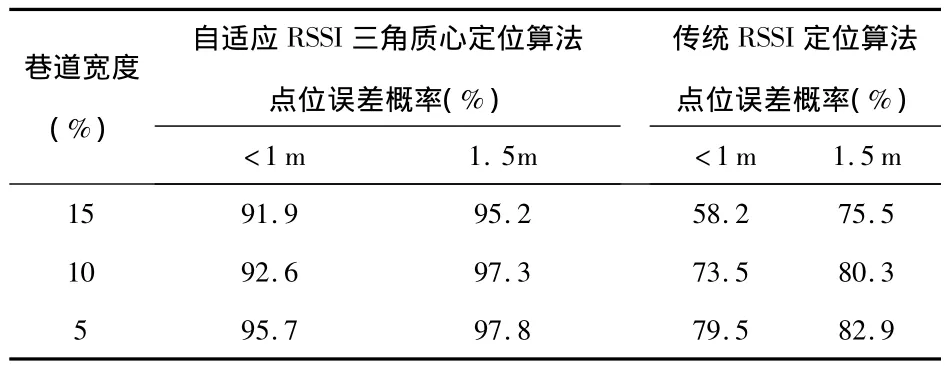
表2 定位算法的点位误差概率比较Tab 2 Comparison of localization error probability of localization algorithms
4 结论
采用自适应RSSI三角质心定位算法,对煤矿井下目标进行定位,不仅可以克服传统RSSI定位算法的缺陷,而且可以较好地适应煤矿井下复杂多变的环境。仿真实验表明:巷道宽度在一定范围内(5~15 m),定位误差平均值均低于0.5 m,定位误差小于1 m的概率均高达90%以上,具有较高的定位精度。
[1]Luthy K A,Grantd E,Henderson T C.Leveraging RSSI for robotic repair of disconnected wireless sensor networks[C]//Proc of 2007 IEEE Int'l Conf on Robotics and Automation,2007:10-14.
[2]Sheu J P,Hu W K,Lin J C.Distributed localization scheme for mobile sensor networks[J].IEEE Transactions on Mobile Computing,2010,9(4):516-526.
[3]Akyildiz L F,Su Wenlian,Sankarasubramania M Y.A survey on sensor networks[J].IEEE Communications Magazine,2011,40(8):102-114.
[4]Heinzelman W R,Chandrakasan A P,Balakrishna N H.Energyefficient communication protocol for wireless microsensor networks[C]//Proc of the 3rd Hawaii International Conference on System Science,Washington DC:IEEE,2010:3005-3014.
[5]Patwari N,Ash J N,Kyperountas S,et al.Locating the nodes cooperative localization in wireless sensor networks[J].IEEE Signal Processing Magazine,2005,22(4):54-69.
[6]王 焱,单欣欣,姜 伟.无线传感网络中移动节点定位技术研究[J].传感技术学报,2011(9):1326-1331.
