六维腕力传感器非线性正解耦方法设计*

陈 峰，徐一鸣，钟永彦，林 纯

（南通大学电气工程学院，江苏南通 226019）

0 引言

多维力传感器是智能机器人重要组成部分，已广泛应用于机器人和遥控操作领域，获取力的变化方向和强度大小是其主要任务。对臂—环境交互的感知能力是机器人由单一的重复行为转变为针对未知环境或任务具有一定自主决策能力的智能体系［1］。多维力传感器应用在可穿戴型助力机器人系统，用于获取人—机交互信息［2］;针对目前常用手写设备信息获取不全面问题，基于多维力传感器设计的笔交互设备能获取手写全力信息［3］。另外，广泛应用于灵巧手的多维指力传感器［4］，使手指实现智能抓取成为现实。

对于多维力传感器而言，一旦受力，弹性体在各个方向上均会产生形变，从而导致各向输出，即使是理想的输入也会产生不期望的结果——耦合误差。解耦方法通常被用来提高输出精确度，避免因耦合误差而引起系统误动作。利用最小二乘法所构建的静态线性解耦方法常应用于工程解耦中［5～8］，其解耦效果的好坏主要依赖于传感器的结构设计、加工工艺等的优劣，该方法的主要优点是便于实现逆解。但在实际应用中，静态线性解耦并不十分理想，其原因在于传感器的输入—输出关系并非是理想的线性关系。为此，有研究人员提出用分段线性化法，因其计算时间太长而无法应用于工程实际中［9］。借鉴风洞天平非线性标定方法，理论上利用多次非线性拟合手段，实现非线性解耦［8］，仿真已证明其可行性。近年来，智能计算被广泛应用于多维力传感器解耦与误差补偿中，借助其良好的非线性逼近能力和自学习能力，通过神经网络和支持向量机等方法重新构建多维力传感器输入—输出关系或进行非线性校正及静态误差补偿［10～13］。

1 静态线性解耦

静态线性解耦方法是在假设传感器各维间是一理想线性关系的前提下，构建关于传感器各通道力/力矩信息与传感器输出信息间的直线方程。传统的静态线性解耦方法可描述为［5］

式中 F为力/力矩向量，U为传感器输出向量，通常是电压信号，C为解耦矩阵。

该方法不足之处在于没有考虑系统的零点输出信息。在此基础上，改进的线性解耦方法［6］得以提出

式中 B为传感器各维和维间的零点信息。

应用该方法时，首先利用标定数据集和常用的最小二乘法完成单维和维间的直线拟合，利用获得的拟合方程系数构建输入—输出耦合矩阵，其次通过解方程，即逆解，通常是对标定的耦合矩阵直接求逆，从而获得解耦矩阵。

为了叙述方便，把文献［5］中的解耦方法暂定为方法1，文献［6］中的解耦方法暂定为方法2，本文中的正解耦方法称为方法3。

2 静态非线性正解耦

因结构设计、加工工艺、敏感元件抗干扰能力、传感器零点漂移等因素，传感器各维力/力矩信息与传感器输出信息之间存在某种非线性关系。实验也证实，有的耦合表现为单调非线性，有的则会出现几个弯［9］。利用多项式方程可以尽量弥补与真实值间的差距。当然，上面提及的传统静态线性解耦方法也可以扩展为多项式方程，利用传统分析方法将六维腕力传感器输入—输出关系扩展为二次曲线形式，如下式所示

式中i，j=1，…，6，FMj为第j项加载（如j=1意味着Fx加载，其它方向无任何加载;j=4意味着Mx加载，其它方向无任何加载），Uij对应第j项加载时产生的6路输出信息。当i=j时，为主输出项;当i≠j时，为耦合输出项。在传感器静态标定完成后，aij，bij和cij可通过最小二乘法求解获得。而每一维的最终输出是其主输出项与耦合输出项之和，即

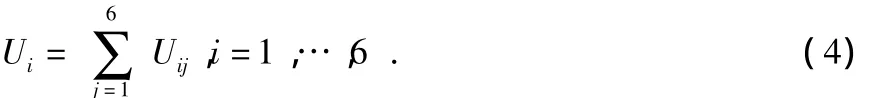
将上式展开可得联立方程

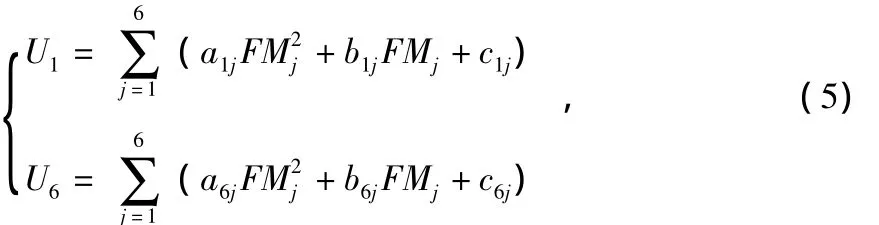
式中aij，bij和cij均为已知系数。该方程组也可以写成矩阵形式

应用时，将测量获得的输出值代入方程式（5）或式（6），解出FM。对于多元高次方程组而言，逆解运算较为因难，主要表现在:

1）即使利用Matlab等计算工具，多元高次方程组的解也需较长时间（当次数大于2时）;

2）力输出的唯一性使在多元高次方程组多解结果中选择其一也较为困难，且需要增加额外的约束条件;

3）方程式（3）的形式越复杂，如增加开方项、指数项或三解函数项等，对应方程式（5）或式（6）的求解就越困难。

但方程式（5）或式（6）的通解形式可表示为

式中fi表示与传感器各维输出项相关的多项式函数，该函数结构形式不唯一，主要由方程式（5）或式（6）的结构形式决定。鉴于此，针对多维力传感器，本文提出非线性正解耦方法，该方法通过直接构造力/力矩信息与输出信息（通常是电压信息）间的关系函数，与传统线性解耦方法相比，方法3无需进行曲线拟合、解方程组，故称该方法为正解耦方法，该方法也无需假定对象是线性系统。以Fx为例，其关系方程可表示为

该方程包含主输出项u1、耦合项ui（i=2，…，6）、交叉耦合项ui·uj（i≠j，i，j=1，…，6）。利用同样方法，可分别构造出 Fy，Fz，Mx，My，Mz。因此，公式（8）经扩展后用矩阵形式表示

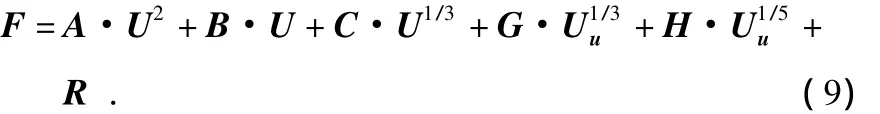
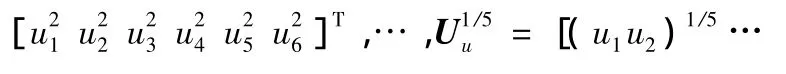
为了方便求解待定系数矩阵 A，B，C，G，H和R，方程式（9）重新改写为

矩阵F和Q的维数由标定数据集确定。根据标定的数据矩阵集和广义逆矩阵中的矩阵右逆，可得解耦矩阵

该方法中，多项式结构的选择及维间交叉项形式与求解解耦矩阵的难易无关，若矩阵Q右逆不存在，可利用Moore-Penrose逆实现最佳最小二乘解。

3 实验结果分析

利用文献［5］中的完整标定数据集（取递增负载与递减负载两者对应输出值之和的均值作为其相应输出值），可得（7）式中的F为6×51矩阵，Q为55×51矩阵。解耦矩阵具体计算步骤如下:

1）提取标定数据集中的力/力矩信息，构造矩阵F∈R6×51，如 Fx=5，扩展为向量［5 0 0 0 0 0］T，如 Fy=5，扩展为向量［0 5 0 0 0 0］T，依此类推;

2）提取标定数据集中的输出信息，构造矩阵 U∈R6×51，其每一列是与步骤（1）中加载项相对应的6路输出信息;

3）计算向量 U2∈R6×51，U（i，j）=U（i，j）·U（j，j）;

4）计算向量 Uu∈R15×51，Uu（m，n）=U（i，n）·U（j，n），i≠j，i，j=1，…，6;

5）计算 U1/3=nthroot（U，3），=nthroot（Uu，3），=nthroot（Uu，5）;

6）构造矩阵

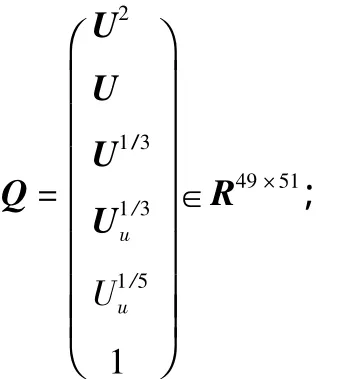
最后获得

针对文献［5］中的标定数据集，分别采用方法1和方法2的解耦结果在文献［6］中已作比较，这里不再赘述。本文仅对方法2与方法3的解耦结果作比较。利用方法2与方法3所获得的解耦结果如附表1和表2所示。表中数据均采用科学表示法。图1是表中主输出项Mz在2种方法下产生的误差柱状图。

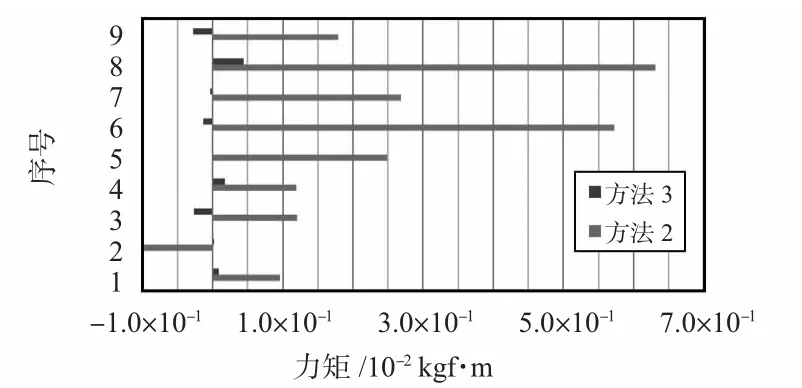
图1 Mz方向上的解耦误差Fig 1 Decoupling error of Mz-axis

4 结论

1）采用非线性正解耦方法，系统输出优于采用传统的线性解耦方法;

2）非线性正解耦无需进行单维和维间的曲线拟合与方程逆解;

3）非线性正解耦方程可根据实际需要，其多项式方程可任意扩展。

考虑到标定时所使用的单位（力:kgf;力矩:kgf·m），方法3也存在解耦不理想情况，如表2中的Mx输出项。

表1 Fz加载，其它方向无加载时解耦结果（力（kgf），力矩（10－2kgf·m））Tab 1 Decoupling results of Fz，no load in other directions（Force（kgf），Moment（10 －2kgf·m））

表2 Mz加载，其它方向无加载时解耦结果 （力（kgf），力矩（10－2kgf·m））Tab 2 Decoupling results of Mzis loaded，no load in other directions（Force（kgf），Moment（10 －2kgf·m））

［1］Bicchi A.A criterion for the optimal design of multi-axis force sensors［J］.Robotics and Autonomous Systems，1992，10（4）:269-286.

［2］陈 峰，余 永，葛运建.基于接触力信息的穿戴型步行助力机器人研究［J］.高技术通讯，2008，18（12）:1269-1273.

［3］罗健飞，吴宝元，申 飞，等.支持笔交互的手写设备设计与实现［J］.仪器仪表学报，2012，3（9）:2215-2124.

［4］张晓辉，高 峰.新型机器人手指六维力传感器设计［J］.传感器技术，2003，22（9）:22-27.

［5］许德章，吴仲城，葛运建，等.机器人六维腕力传感器耦合矩阵的确定与摄动分析［J］.仪器仪表学报，2005，26（1）:75-81.

［6］张景柱，郭 凯，徐 诚.六维力传感器静态解耦算法应用研究［J］.传感器与微系统，2007，26（12）:58-59（62）.

［7］刘广孚，张为公，李忠国.多维车轮力传感器静态耦的研究［J］.仪表技术与传感器，2006（7）:15-18.

［8］徐科军，李 成.多维腕力传感器静态解耦的研究［J］.合肥工业大学学报:自然科学版，1999，22（2）:1-6.

［9］王国泰，易秀芳，王理丽.六维力传感器发展中的几个问题［J］.机器人，1997，19（6）:474-478.

［10］姜 力，刘 宏，蔡鹤皋.多维力/力矩传感器静态解耦的研究［J］.仪器仪表学报，2004，25（3）:284-287.

［11］曹会彬，孙玉香，刘利民，等.多维力传感器耦合分析及解耦方法的研究［J］.传感技术学报，2011，24（8）:1136-1140.

［12］李海滨，段志信，高理富，等.基于神经网络的六维力传感器静态标定方法研究［J］.内蒙古工业大学学报，2006，25（2）:85-89.

［13］刘 涛，王 华.传感器非线性校正的遗传支持向量机方法［J］.电子测量与仪器学报，2011，25（1）:56-60.