薄互层AVO 响应特征分析*

佘钰蔚，朱仕军，朱鹏宇，党洲涛，唐绪磊，杨维磊，胡桂林

(1.西南石油大学 地球科学与技术学院，四川 成都610500;2.中国石油川庆钻探工程公司地球物理勘探公司，四川 成都610213;3.中国石油长庆油田公司，陕西 西安710018)

0 引 言

AVO(amplitude versus offset)技术依据振幅随炮间距的变化规律所包含的储层岩性及其孔隙流体的性质的信息，能直接进行油气预测［1］。1984年Ostander［2］提出AVO 技术后，作为一种重要的流体检测工具，得到了迅速的发展和应用［3-4］。其中，Zoeppritz 方程［5］是传统AVO 的理论基础，Shuey 两项近似式［6］的出现，促使AVO 技术有革命性的发展。在近角度情况下截距和梯度能较好的刻画AVO 特征，是岩石骨架、孔隙度及孔隙流体的综合响应，其交会图分析技术能直观简单的刻画含气性，因此在储层预测中被广泛使用［7-8］。

中国油气田多发育薄层或薄互层储层，随着油气勘探和开发的不断深入，砂泥岩薄互层储层无疑会成为勘探重点。近年来，Bakke［9］，Yinbin Liu［10］，Jingye Li［11］，姚 陈［12］、周 丽［13］，Wenyong Pan［14］等学者在单一薄层AVO 响应特征方面取得了许多重要成果，这些成果为地层中单一薄层流体检测定性解释奠定了良好的基础，但作为地层中沉积更为普遍更具工业开采价值的地质结构——砂泥岩薄互层，因其组合关系多，内部结构多样，AVO 响应复杂，导致相关的研究相对较少［15］，因此对薄互层的AVO 响应特征进行研究具有重要的意义。

薄互层的顶底界面是决定反射特征的主要因素，利用已知的等厚薄互层岩性、油、气和水的模型，分别在声学介质和弹性介质条件下进行数值模拟，优选出更能精确刻画厚薄互层顶界面AVO响应特征的数值模拟方法。从而采用该波动方程进一步研究薄层数和单层厚度对薄互层截距、梯度及其交会属性的影响规律，有助于从实际叠前地震数据中识别含气薄互层有利区，提高储层预测的精度。

1 正演模拟

设计如图1 所示的地质模型，该模型由均匀泥岩背景中包含不同互层数的砂泥岩等厚薄互层地质体组成，砂泥岩的互层数分别设定为:1，2，4，6，8，10，借以考察不同互层数对薄互层的AVO 响应的影响。其中砂岩骨架Vp=6 000 m/s，Vs=3 000 m/s，ρ=2.65 g/cm3. 泥岩阻抗为储层骨架阻抗的80%.地震子波采用零相位雷克子波，主频为30 Hz.采用交错有限差分法正演模拟获取单炮记录;采取中间放炮、两边接收的的采集方式，地震道采样点数为4 000，采样间隔0.001 s，道间距20 m，共400 道，单层厚度从1 以2 m 为间隔变化到35 m.对孔隙度12%，含气饱和度80%的储层模拟了这6 种薄互层模型得到108 套地震数据体。

2 声学介质与弹性介质

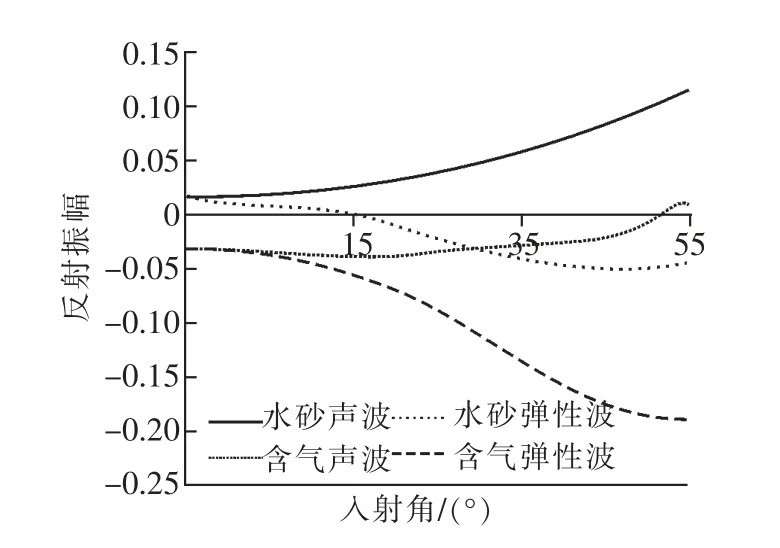
Yinbin Liu 和Schmitt［7］已研究单一薄层在声学介质下的AVO 响应。Wenyong Pan 和Kristopher A［11］在前者的基础上，进行单一薄层在弹性介质下的AVO/AVF 特征研究，表明声学介质不适合单一薄层AVO 研究。类似的，针对薄互层的AVO 响应，利用Grassmann 方程进行流体替代，分别在声学介质和弹性介质下，设计等厚四层5 m 地质模型(参数表(1))进行数值模拟。在0°入射的情况下，声学介质和弹性介质下砂岩顶界面的振幅值基本相同。然而，当入射角大于20°两种介质情况下AVO 差异越来越明显。含水砂岩薄互层的情况下，声学介质中振幅随入射角增大出现了砂岩底界面假亮点的现象，而弹性介质中出现第二类AVO 响应。将含水砂岩替换成含气砂岩后，声学介质中在50°出现极性反转的现象，而弹性介质则无此现象。因此，在预测流体性质时上述解释陷阱的出现表明在进行薄互层的AVO 分析时采用弹性介质更加精确。

3 数据分析与认识

3.1 薄互层AVO 特征与互层数之间的关系

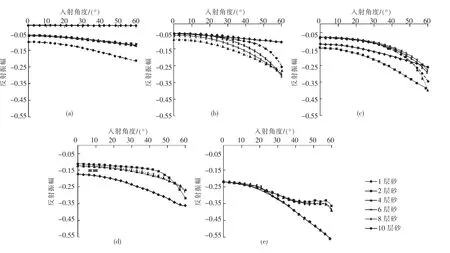
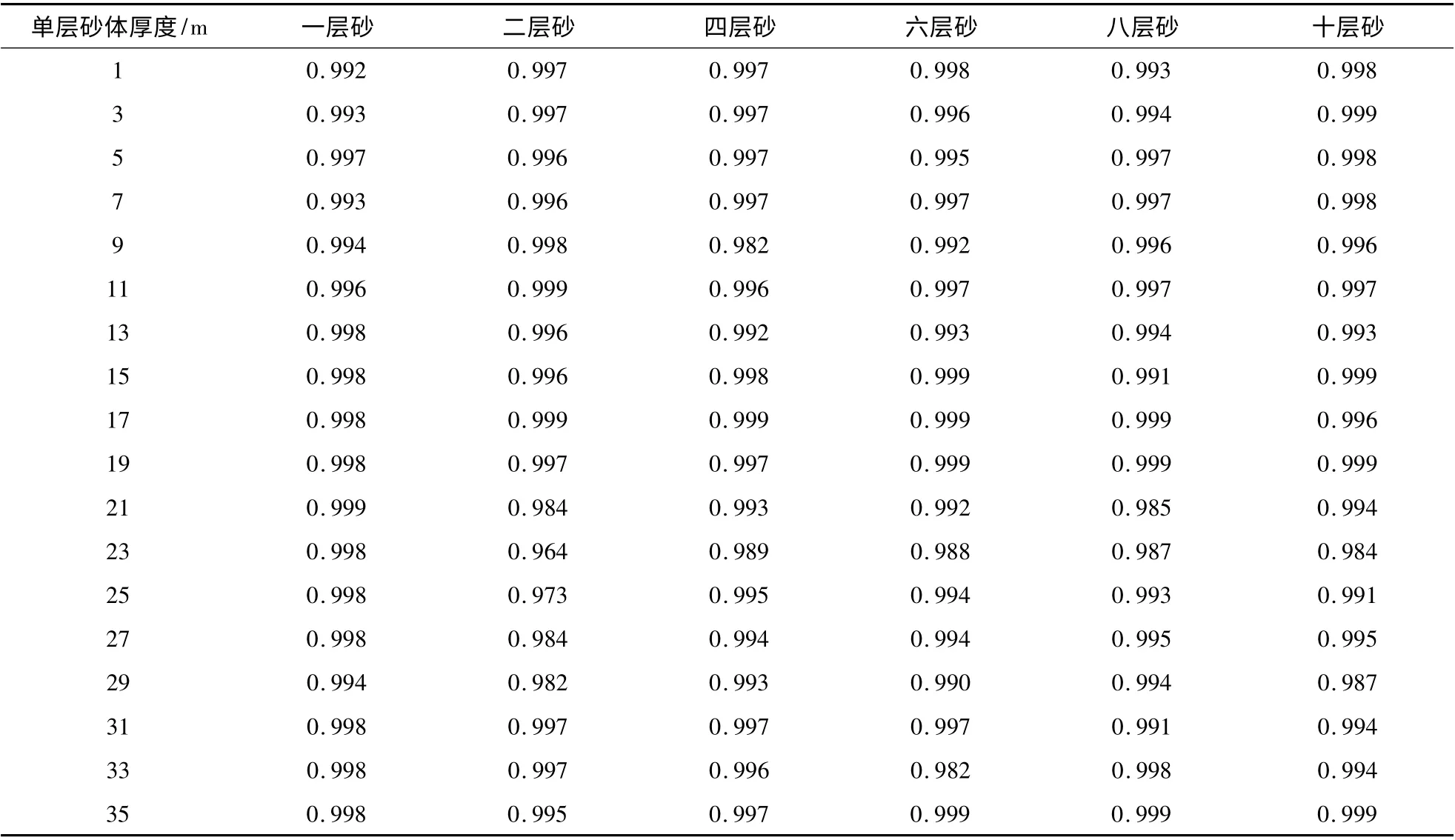
从盖层为储层骨架阻抗的80%，储层孔隙度为12%，含水饱和度为20%的等厚薄互层弹性波动方程正演结果图3 分析，薄互层仍然能产生清晰的AVO 异常，且具有一定的规律。因此能够利用薄互层AVO 响应特征进行烃类检测。为刻画薄互层振幅随偏移距变化的特征，采用Shuey 两项式的思想，把sin2(θ)视为变量，对0° ～30°的薄互层AVO 响应进行线性拟合。从表2 知拟合相关系数均大于0.973，由此说明截距和梯度仍然可以描述近角度入射情况下薄互层AVO 的特征。

单层砂体厚度/m 一层砂 二层砂 四层砂 六层砂 八层砂 十层砂0.992 0.997 0.997 0.998 0.993 0.998 3 0.993 0.997 0.997 0.996 0.994 0.999 5 0.997 0.996 0.997 0.995 0.997 0.998 7 0.993 0.996 0.997 0.997 0.997 0.998 9 0.994 0.998 0.982 0.992 0.996 0.996 11 0.996 0.999 0.996 0.997 0.997 0.997 13 0.998 0.996 0.992 0.993 0.994 0.993 15 0.998 0.996 0.998 0.999 0.991 0.999 17 0.998 0.999 0.999 0.999 0.999 0.996 19 0.998 0.997 0.997 0.999 0.999 0.999 21 0.999 0.984 0.993 0.992 0.985 0.994 23 0.998 0.964 0.989 0.988 0.987 0.984 25 0.998 0.973 0.995 0.994 0.993 0.991 27 0.998 0.984 0.994 0.994 0.995 0.995 29 0.994 0.982 0.993 0.990 0.994 0.987 31 0.998 0.997 0.997 0.997 0.991 0.994 33 0.998 0.997 0.996 0.982 0.998 0.994 1 35 0.998 0.995 0.997 0.999 0.999 0.999

3.1.1 截距

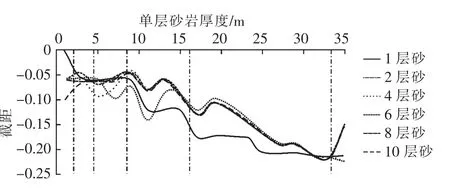
单一薄层法线入射时AVO 的截距和梯度的绝对值与砂体厚度密切相关。当砂体厚度小于1/64波长时，没有AVO 响应;小于1/4 波长范围内，单一砂体法线入射时AVO 的截距和梯度的绝对值随着砂体厚度的增加单调递增(图4)。

等厚薄互层顶界面AVO 的截距绝对值也与互层数密切相关。当单层厚度小于1/64 波长时，单一薄砂层没有AVO 响应，但单层厚度小于1/64 波长的多个薄互层也可形成较强的AVO 响应(图3(a)、图4)。当单层厚度大于1/64 波长且小于1/8 波长时，单一砂体厚度下，截距绝对值随互层数的增加，呈调谐效应，先增加后减小，调谐振幅大于单一薄层时的振幅值(图3(b)、图4)。其中1/32 到1/27 波长之间4 层薄互层处在调谐厚度;1/27 到1/10 波长之间2 层薄互层处在调谐厚度。因此，薄互层随着单层砂体厚度增加，出现调谐截距的层数在递减。当单层厚度大于1/8 波长且小于等于1/4 波长时，薄互层截距几乎不受砂体层数的影响，且薄互层截距一般小于单一薄砂岩截距值(图3(e)、图4)。

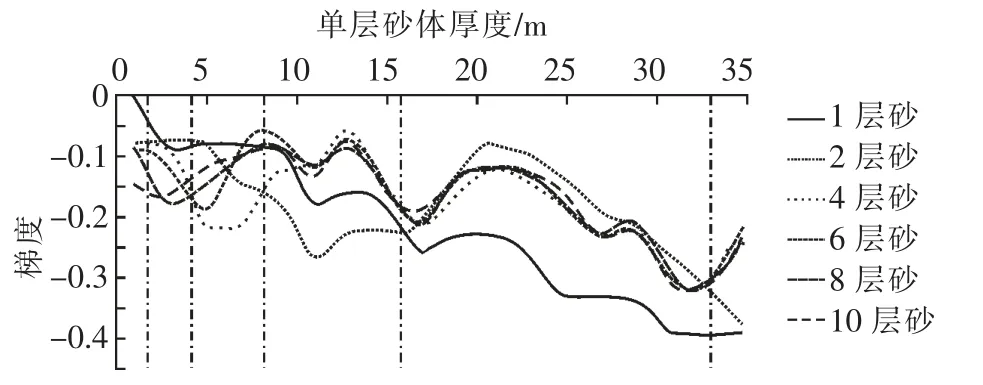
3.1.2 梯度

等厚薄互层顶界面AVO 的梯度绝对值也与互层数密切相关。当单层厚度小于1/64 波长时，10层截距和梯度值最大(图4，图5)。当单层厚度大于1/64 波长且小于1/8 波长时，固定单层砂体厚度时，薄互层梯度绝对值随互层数的增加，呈调谐效应，先增加后减小，调谐梯度大于单一薄层时的梯度值(图3(b)、图5)。其中1/64 到1/32 波长8层薄互层产生调谐梯度;1/32 到1/16 波长之间4层薄互层处在调谐厚度，出现梯度最大值;而1/16到1/8 波长之间2 层薄互层产生调谐梯度。因此，薄互层随着单层砂体厚度增加，出现调谐梯度的层数在递减。当单层厚度大于1/8 波长且小于1/4 波长时，梯度几乎不受互层数的影响，且薄互层梯度小于单一薄砂岩梯度值(图3(d)、图5)。

薄互层梯度与截距变化大体趋势相似，但又有区别。随着薄互层单层砂体厚度增加，出现调谐梯度和梯度的层数均在递减，且截距变小更快。单层砂岩厚度大于1/8 波长后，梯度不受薄互层层数的影响，而截距出现在1/10 波长处。因此，截距对薄互层单砂岩厚度更加敏感。与单砂体进行对比，受薄互层单层厚度和层数变化的调谐影响，薄互层单层厚度小于1/8 波长时，薄互层调谐截距和梯度均大于等于单砂岩的值，对AVO 效应起到加强的作用，更易识别;但当薄互层单层厚度大于1/8 波长小于1/4 波长时，AVO 效应较单层砂岩相同厚度时减弱。

3.2 薄互层P-G 交会属性特征

经上述薄互层截距和梯度随单层厚度变化特征分析知，可按照截距的变化规律，将小于1/4 波长单层厚度分为5 个区间，即(0，1/64)(1/64，1/32)(1/32，1/16)(1/16，1/8)(1/8，1/4)，且每个区间内薄互层截距和梯度随互层数的变化规律基本一致。因此，可按照单层砂体厚度将小于1/4 波长薄互层按区间划分为5 种类型。寻找该5 种类型薄互层的规律，便能指导划分出有利含气区域。因此，分别进行单层厚度1，5，11，21 和33 m 的薄互层进行P-G 交会属性研究。

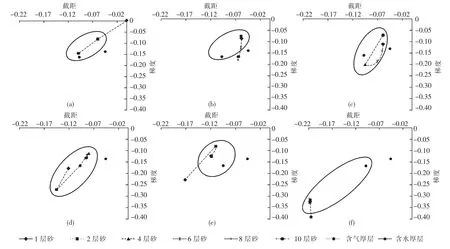
将5 种含气薄互层与含气厚层和含水厚层进行对比(图6)，发现薄互层在P -G 交会图上分布具有一定的规律。当薄互层单砂体厚度落入(0，1/64)波长，含气薄互层P -G 分布在厚层的右上方黄色区域(图6(a))。当薄互层单砂体厚度为(1/64，1/32)波长时，含气薄互层P -G 分布在厚层的右上方黄色区域，非常接近含水厚层位置(图6(b))。而单砂体厚度落入(1/32，1/16)波长范围内，含气薄互层P-G 分布在厚层的右下方黄色区域，接近含水厚层位置(图6(c))。当单砂体厚度为(1/16，1/8))波长时，含气薄互层P -G 分布以厚层为中心的黄色区域(图6(d))，开始远离含水厚层区域。当单砂体厚度落入(1/8，1/4)波长时，含气薄互层P-G 分布在厚层左上方黄色区域(图6(e))，远离含水厚层。最后，当薄互层单砂体厚度等于1/4 波长时，含气薄互层P-G 略小于单层含气砂岩，且远离含气厚层和含水厚层，出现典型的Ⅲ类AVO 现象，有利区分布在厚层左下方黄色区域(图6(f))。由此说明，随着薄互层单层厚度的增加，P-G 由右上区域变化到左下区域。

4 实际资料的分析

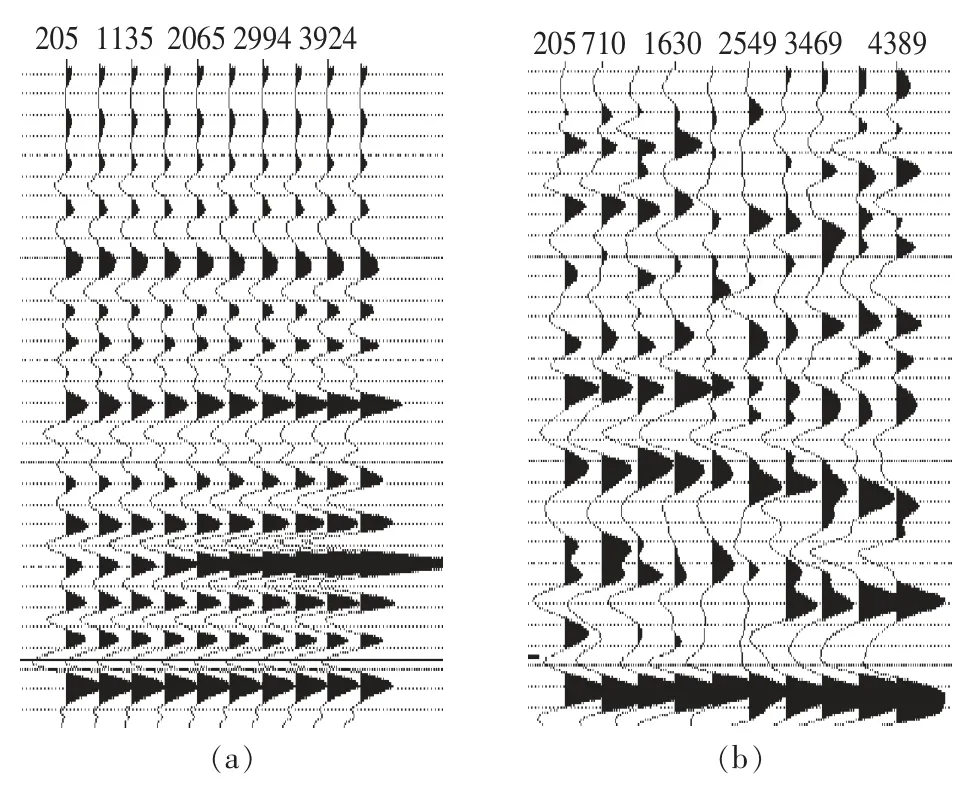
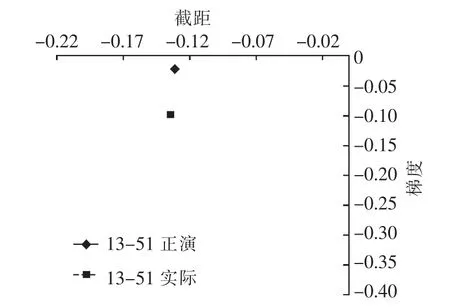
选择苏里格地区某气田高产气井13 ～51 井，进行AVO 正演模拟研究。该井储盖条件、含气饱和度和孔隙度与设计模型大致相当，13 ～51 井具有2 层约21 m 的砂岩储层。其正演模拟及实际井旁的地震偏移距道集和P -G 交会图分别如图7，图8 所示。可以看出13 -51 井正演模拟及实际井旁道集的P-G 属性均分布在左上区域，与设计模型单层厚度为21 m 时P -G 属性(图6(e))分布规律一致。

5 结 论

1)进行薄互层的AVO 数值模拟分析时声学介质条件下会出现假亮点，在弹性介质中进行数值模拟更加合理;

2)薄互层单层厚度小于1/8 波长时，P -G 均大于等于单层砂相同厚度的P-G 值，薄互层对顶面AVO 效应起到加强的作用。当薄互层单层厚度大于1/8 波长小于1/4 波长时，AVO 效应较薄层情况减弱;

3)随着薄互层单层厚度的增加，P -G 由右上区域变化到左下区域，有一定的分布规律。因此可以根据工区薄互层单层厚度和层数确定出薄互层发育的P-G 属性的分布范围，从而指导储层预测，为勘探开发提供依据;

4)实际井资料正演模拟及实际井旁道集的P-G 属性均分布在左上区域，分布规律一致。

References

［1］ 孙鹏远.AVO 技术新进展［J］. 勘探地球物理进展，2005，28(6):432 -438.SUN Peng-yuan.Advances in AVO techniques［J］.Progress in Exploration Geophysics，2005，28(6):432 -438.

［2］ Ostrander W.Plane-wave reflection coefficients for gas sands at nonormal angles of incidence［J］. Geophysics，1984，49(6):1 637 -1 648.

［3］ Rutherford Williams.Amplitudes-versus-offset in gas sands［J］.Geophysics，1989(26):138 -157.

［4］ 王宝江，李 美，于 强，等. 复杂气藏AVO 属性交会含气性检测应用研究［J］.地球物理学进展，2013，28(1):310 -319.WANG Bao-jiang，LI Mei，YU Qiang，et al. Predicting ans detecting of the gas sand by AVO attributes crossplot in complex reservoir［J］.Progress in Geoghys，2013，28(1):310 -319.

［5］ Zoeppritz K，Uber Erdbebenwellen.On the reflection and propagation of seismic waves［J］. Gottingen Nachricten der Konigl，1919(2):66 -84.

［6］ Shuey R T. A simplification of the Zoeppritz equations［J］.Geophysics，1985，50(4):539 -546.

［7］ 潘仁芳，陈思路，张利萍，等. 含气砂岩AVO 正演的半定量分析［J］. 石油地球物理勘探，2013，48(1):103 -108.PAN Ren-fang，CHEN Si-lu，ZHANG Li-ping，et al.Semi-quantitative analysis of gas bearing sand by AVO forward modeling［J］.Oil Geophysical Prospecting，2013，48(1):103-108.

［8］ 张德英，陈全红.叠前弹性波阻抗反演技术在赤道几内亚X 区块储层预测中的应用［J］.西安科技大学学报，2013，33(2):173 -177.ZHANG De-ying，CHEN Quan-hong.Application of prestack elastic wave impedance inversion technique in reservoir prediction of X block in equatorial guinea［J］.Journal of Xi’An University of Science and Technology，2013，33(2):173 -177.

［9］ Bakke N E，Ursin B.Thin-bed AVO effects［J］.Geophysical Prospecting，1998，46(6):571 -587.

［10］LIU Y，Schmitt D R.Amplitude and AVO responses of a single thin bed［J］. Geophysics，2003，68(4):1 161 -1 168.

［11］LI Jing-ye，CHEN Xiao-hong.Seismic AVO modeling and analysis for thin inter-layer reservoir［C］//SEG Houston 2009 International Exposition and Annual Meeting，2009:316 -320.

［12］姚 陈，蔡明刚，王 贽.各向同性薄层反射理论地震图［J］.地球物理学报，2010，53(1):164 -170.YAO Chen，CAI Ming-gang，WANG Zhi. Synthetic seismograms of reflection from isotropic thin layer［J］.Chinese Journal of Geophysics，2010，53(1):164 -170.

［13］周 丽，顾汉明，马灵伟，等.基于波动方程正演模拟分析薄砂层含不同流体的AVO 特征［J］. 地质科技情报，2013，32(2):169 -173.ZHOU Li，GU Han-ming，MA Ling-wei，et al.Analysis of AVO characteristics on thin san reservoir with various fluid based seismic modeling［J］. Geological Science and Technology Information，2013，32(2):169 -173.

［14］ PAN Wen-yong，Kristopher A. AVO/AVF analysis of thin-bed in elastic media［J］.SEG Houston 2013 Annual Meeting，2013:373 -377.

［15］赵 伟，陈小宏，李景叶.薄互层调谐效应对AVO 的影响［J］.石油物探，2006，45(6):570 -573.ZHAO Wei，CHEN Xiao-hong，LI Jing-ye. Analysis of impact of thin effect on AVO［J］.Geophysical Prospecting for Petroleum，2006，45(6):570 -573.