微波照射下岩石损伤细观模拟分析*

戴 俊，秦立科

(西安科技大学 建筑与土木工程学院，陕西 西安710054)

0 引 言

微波加热具有很多传统加热所不具有的优点，如快速加热、内部加热、选择性加热等，使得微波加热在食品、医疗、冶金等各个领域有着广泛地应用。微波加热同样可以用于岩石破碎［1-2］，该方法属于热能破岩的一种，其过程是先利用微波照射岩石然后再利用机械进行破碎［3］。该方法的实质是利用微波加热的选择性，使得岩石不同成分产生差异膨胀，在岩石内部形成微裂纹，增加岩石的节理面，降低岩石的硬度和强度［4-5］，从而有效地提高后期机械破岩的效率，降低破岩的能耗和设备的磨损［6-7］。此外，微波加热的高效性及过程易于控制等特点，使得微波辅助破岩更具有广阔的应用前景［8-9］。F.Hassani［10］对不同地区的玄武岩进行了微波照射试验，结果表明微波照射可以减低岩石的抗拉和抗压强度，微波功率越大和照射时间越长而强度降低的幅度越明显。戴俊［11］对陕西的花岗岩进行了照射试验，试验结果表明微波照射后花岗岩的抗拉强度有较大幅度的降低，有的甚至可达40%，这说明微波预处理可以有效地降低岩石的强度从而有助于岩石的破碎。目前，该领域研究主要是采用实验手段分析对比微波照射前后岩石的宏观力学性能的变化，而对岩石内部细观性能变化研究较少。为此，文中以吸波的黄铁矿和透波的方解石所组成的岩石颗粒为研究对象，基于热力耦合采用有限差分法对微波场中岩石颗粒的屈服区域的分布及变化进行研究分析，以期进一步弄清微波照射岩石的损伤规律。

1 计算方法

微波照射物体所产生的热量主要取决于微波的频率、电场强度及物体的介电性质，物体单位体积产生的热量可以通过如下公式进行计算

式中 Pd是微波的功率密度，W/m3，即微波转化为热量的功率;f 是微波的发散频率，Hz;ε0为真空介电系数(8.854 ×10-12F/m);εr″为介质的介电损耗因子;E 为电场有效值，V/m.

由于介电性质的不同，大多数的硫化矿和一些氧化矿及化合物能很好的吸收微波，可以在很短时间内吸收微波能量并升温。而与矿物共生的脉石成分，如石英和方解石则几乎不能被微波加热［12-13］。在常温下，方解石的介电损耗因子约为4 ×10-4，黄铁矿为17，所以在计算时可以认为方解石在微波照射下没有热量产生。

在有限元计算时，能量平衡可以用如下的公式表示

式中 qi，j是热通量向量，W/m3，可以由傅里叶定律求得;qv是微波照射所产生的热量，W/m3;ρ 为材料的密度，kg/m3;C 是材料的比热容，J/kg℃.其中，qv即为是微波的功率密度。

将式(1)代入式(2)可以写成

在微波照射过程中，材料内部任意位置的温度变化都可以通过上式计算得出。

材料在微波加热后，温度变化所引起的应变可以表示为

式中 εi，j为应变;αi，j是热膨胀系数，1/℃;ΔTi，j温度变化。

由热量产生的应力可以通过胡克定律计算

式中 σi，j是单元i，j 的热应力;Ei，j是单元i，j 的弹性模量，Pa;vi，j是单元i，j 的泊松比。

2 计算模型

计算模型如图1 所示，岩石颗粒由方解石和黄铁矿组成，大小为1 mm ×1 mm，中间黄铁矿晶体的大小为0.2 mm×0.2 mm.模型简化为二维应力模型进行计算，单元长度为0.01 mm，划分后单元共10 000 个单元。采用FLAC2D5.0 进行计算。

计算假定:①模型边界为自由边界，与周围绝热;②黄铁矿与方解石固定接触;③黄铁矿为吸波材料，在微波场中产生热量，而方解石为透波材料不发热。

图1 计算模型Fig.1 Geometric plot of computed model

黄铁矿及方解石的热学参数见表1 和表2［14］，力学参数见表3［15］。计算时，岩石颗粒的初始温度取室温25 ℃.黄铁矿和方解石本构模型采用应变软化模型。

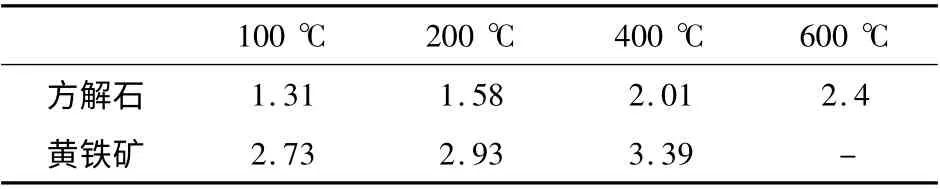
表1 矿物热膨胀系数(10 -5)Tab.1 Thermal expansion coefficient as a function of temperature

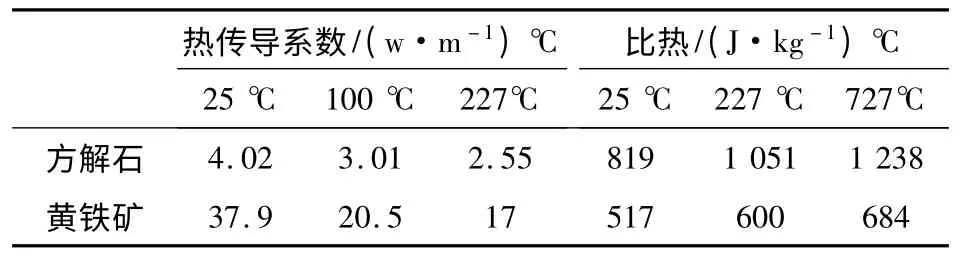
热传导系数/(w·m -1)℃比热/(J·kg -1)℃25 ℃ 227 ℃ 727℃方解石25 ℃ 100 ℃ 227℃4.02 3.01 2.55 819 1 051 1 238黄铁矿37.9 20.5 17 517 600 684

表3 矿物力学参数Tab.3 Mechanical properties of the minerals

3 计算结果与分析

3.1 微波照射时间对颗粒损伤的影响

图2 给出了微波功率密度Pd=1010W/m3照射时间从0.005 到0.035 s 岩石颗粒屈服单元分布图，从图中可以看出，在照射极短的时间内，岩石颗粒内部便发生了屈服，说明了微波加热的高效性。在微波场中岩石颗粒的屈服主要发生在方解石内部，而黄铁矿晶体发生屈服较少。岩石颗粒的屈服类型，既有有剪切屈服也有拉伸屈服，在岩石颗粒的对角方位以剪切屈服为主，而水平及竖直中心线方位以拉伸屈服为主。黄铁矿晶体周围的屈服从四个角点开始，随着照射时间的增加沿两种矿物的交界发展，最终闭合形成沿晶破坏。

图3 给出了岩石颗粒屈服面积所占总面积的百分比随着照射时间变化的关系曲线。从图中可以看出，在照射时间为0.005 到0.03 s 的区间内，岩石颗粒的屈服面积占总面积不到5%，但是已经在岩石颗粒内部形成接近贯通发散状屈服带，这将大大降低岩石的强度。从图中还可以看出，在照射过程中岩石颗粒的拉伸屈服所占的比率比剪切破坏所占的比率要大，随着照射时间增加，无论是拉伸屈服面积还是剪切屈服面积都越来越大。

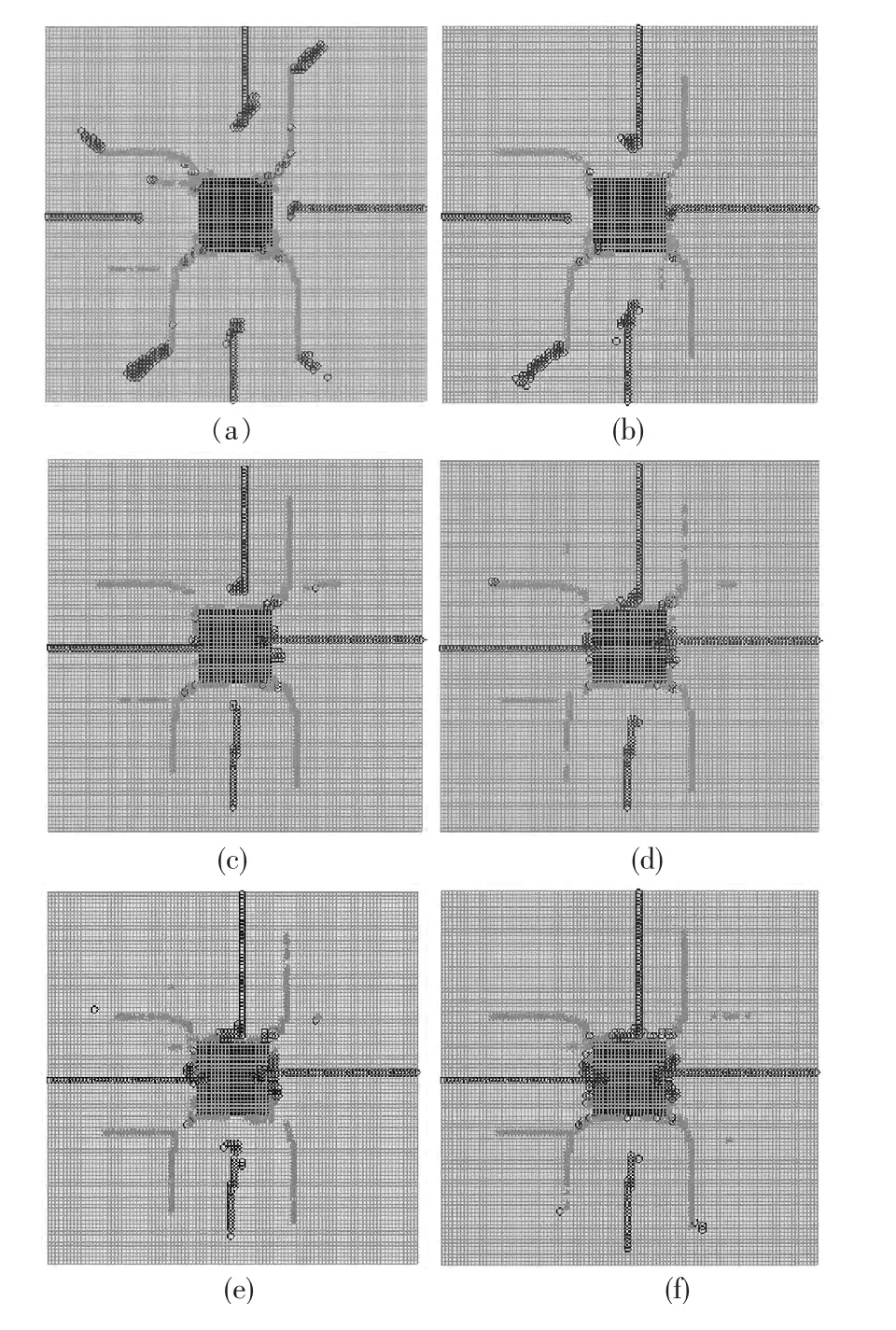
图2 不同照射时间屈服分布图(Pd =1010 W/m3)Fig.2 Yield contour plot of whole model with irradiation time

图3 屈服率随照射时间变化曲线(Pd =1010W/m3)Fig.3 Yield changing versus irradiation time

3.2 矿物晶体大小对岩石颗粒损伤的影响

图4 给出黄铁矿晶体为0.2，0.4，0.6，0.8 mm微波照射0.01 s 后岩石颗粒屈服单元分布图。从图中可以看出，随着晶体颗粒的增大，岩石颗粒中的拉伸屈服所占的比率越来越大，说明晶体颗粒的大小影响岩石颗粒的屈服类型，晶体颗粒尺寸小于0.5 mm 以剪切屈服为主，晶体大于0.5 mm的以拉伸屈服为主。从图中还可以看出，随着黄铁矿晶体的增大，两种矿物交界处屈服的单元越多，越容易形成贯通的裂纹。主要是由于晶体颗粒越大，吸收的热量越多，温度越高，产生的温度应力差越大。

图4 不同晶体大小屈服分布图(Pd =1010W/m3，t=0.01 s)Fig.4 Yield contour plot of whole model with size of pyrite(a)0.2 mm (b)0.4 mm (c)0.6 mm (d)0.8 mm

4 结 论

1)岩石颗粒对角线方向以剪切屈服为主，而在中心线方向以拉伸屈服为主。黄铁矿晶体周围的屈服从四个角点开始，随着照射时间的增加沿两种矿物的交界发展，最终闭合形成沿晶破坏;

2)随着微波照射时间的增加，岩石颗粒的屈服面积越来越大;岩石颗粒的屈服面积占总面积虽然很小，但在岩石颗粒内部能形成接近贯通发散状屈服带，这将大大降低岩石的强度;

3)晶体颗粒的大小影响岩石颗粒的屈服类型，晶体小以剪切屈服为主，晶体大的以拉伸屈服为主。在同样的条件，晶体大的颗粒更易形成贯通的沿晶屈服带。

References

［1］ Kingman S W，Rowson N A. Microwave treatment of minerals-a review［J］. Minerals Engineering，1998(11):1 081 -1 087.

［2］ Kingman S W，Vorster W，Rowson N A. The influence ofmineralogy on microwave assisted grinding［J］. Minerals Engineering，2000，13(3):313 -327.

［3］ Lindroth D P，Berglund，W R.Microwave assist ed drilling in hard rock［J］. Tunnels ＆ Tunnelling，1993(12):54 -59.

［4］ Chunpeng L，Yousheng X，Yixin H.Application of microwave radiation to extractive metallurgy［J］. Journal of Materials Science and Technology，1990，6(2):121-124.

［5］ Clark D E，Folz D C. Processing materials with microwave energy［J］. Materials Science ＆ Engineering，2000，28(7):153 -158.

［6］ Edelbro C. Rock mass strength-a review［J］. Technical Report，2003(16):1 402 -1 536.

［7］ McGill S L，Walkiewicz J W，Smyres G A.The effect of power level on the heating rate of selected chemical and minerals［J］.Materials Research Society Symposia Proceedings，1998(124):247 -252.

［8］ Kingman S W，Jackson K. Recent developments in microwave-assisted combination［J］. International Journal of Mineral Processing，2004(74):71 -83.

［9］ Holman B W.Heat treatment as an agent in rock breaking［J］.Trans IMM，1927(36):219.

［10］ Hassani F，Nekoovaght P M.Microwave assisted mechanical rock breaking［C］//Harmonising Rock Engineering and the Environment.London:Taylor and Francis Group，2011.

［11］ 戴 俊，孟 振，吴炳权.微波照射对岩石强度的影响研究［J］.有色金属，2014(3):32 -36.DAI Jun，MENG Zhen，WU Bing-quan.Study on impact of rock strength by microwave irradiation［J］. Nonferrous Metals Engineering，2014(3):32 -36.

［12］ Chen T T，Dutrizac J E，Hague K E，et al.The relative transparency of minerals to microwave radiation［J］.Canadian Metallurgical Quarterly，1984，23(3):349 -354.

［13］ Harrison P C.A fundamental study of the heating effect f 2.45 GHz microwave radiation on minerals［D］. Birmingham:University of Birmingham，1997.

［14］ Salsman J B，Williamson R L，Tolley W K，et al.Short pulse microwave treatment f disseminated sulphide ores［J］.Minerals Enginnering，1996，9(1):43 -54.

［15］ Touloukian Y S，Ho C Y. Physical properties of rocks and minerals［M］.NewYork:McGraw Hill，1981.