海积软土次固结性状的试验研究

丁荣祥，张超杰，陈式华，魏海云

(浙江省水利河口研究院，浙江 杭州 310020)

1 问题的提出

饱和软黏土的一维压缩主要由2部分组成:一部分是由于在总应力不变的情况下，随着孔隙水的排出，有效应力逐渐增大，从而导致土体骨架的压缩，这一部分被称为主固结;另一部分则由于土颗粒的塑性调整而导致的土骨架流变特性而引起，由于具有流变特性，土骨架在有效应力不变的情况下也会产生压缩，这种压缩被称为次压缩(或次固结)。Bjerrum(1967年)［1］、Crawford(1985年)［2］指出土体在受荷之后便会立即产生次压缩变形，而不只是在主固结结束后产生。这个观点符合土体这一具有流变特性的工程材料的力学特性并已被工程界广泛接受。本文通过对海积软土的多级加荷一维固结蠕变试验，研究与流变关系密切的次固结系数的变化和能够减少软土流变沉降的加载历时。

2 试验方案

试验仪器采用有侧限的常规固结压缩仪，土样面积为30cm2，高度为2cm，共进行2组8个土样的一维压缩试验。土样取自温岭市东海塘南片综合开发区3-5淤泥质粉质黏土层，取样深度19.2～19.7m，为了确保8个土样性质均一、扰动少，2组取样的钻孔间距3m，并采用了用薄壁取土器取样，此外，试样运输和切割也尽量采取措施减少试样的扰动，因此这8个试样的性质基本是均一的。土样的主要物理力学指标为:ω=45%，Sr=100%，e0=1.007;压缩 (固结):αv0.1～0.2=1.245MPa-1，Esv0.1～0.2=2.14MPa，Cv0.2=1.067×10-3cm2/s;渗透:kh=2.7×10-7cm/s。试验方案见表1。

表1 试验方案表

3 压缩曲线形式与加荷比的关系

许多试验表明，加荷比对固结时间过程曲线的影响是非常显著的。Leonards(1964年)根据曲线形状将其分为主次固结阶段之间有一明显最大曲率点的Ⅰ型、主次固结阶段无法明显分开的Ⅱ型和二者的过渡型Ⅲ型3种类型。从试样zk5-8-5、zk5-8-6、zk5-8-7和zk5-8-8在荷载300kPa下持续26d后，分别施50，100，200，500kPa等不同荷载增量后的变形曲线可以看出 (见图1～4)，本试验土样也呈现出了这一规律。从荷载和结构屈服应力的关系来看，如果荷载远小于结构屈服应力，则压缩曲线为Ⅱ型;如果荷载接近结构屈服应力，则压缩曲线为Ⅲ型;如果荷载远大于结构屈服应力，则压缩曲线为Ⅰ型。

图1 试样zk5-8-5固结蠕变试验图

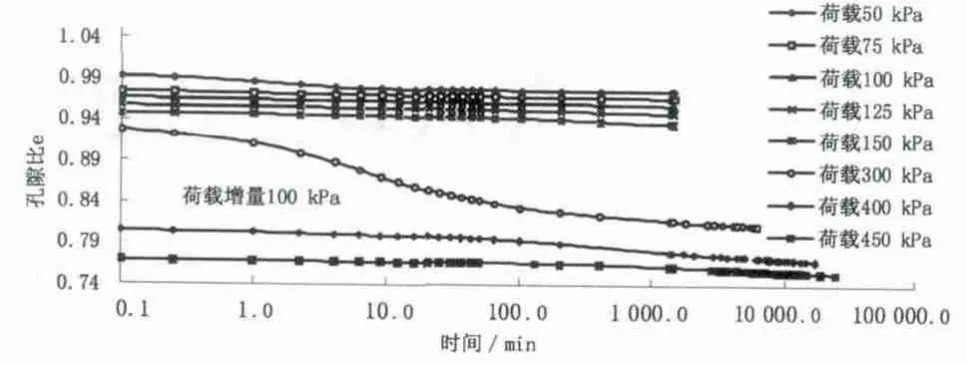
图2 试样zk5-8-6固结蠕变试验图

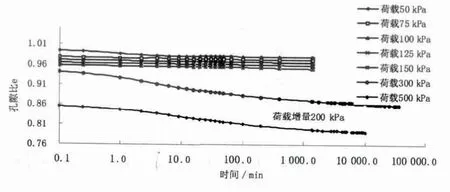
图3 试样zk5-8-7固结蠕变试验图

图4 试样zk5-8-8固结蠕变试验图

4 次固结系数的变化

关于次固结系数的变化，可以从2个角度来观察:一是不同初始状态和荷载增量下，荷载持续某一固定时间内的次固结系数变化;二是同一荷载下，不同时间段内的次固结系数的变化。

图5和图6是试样zk5-8-4的e-log(P)曲线和e-log(t)曲线，图7是不同初始状态和荷载增量下，荷载持续24h内的次固结系数变化。可以看出，在荷载达到结构屈服应力之前，e-log(t)曲线平缓，蠕变速率较低，土体的变形较小;在达到结构屈服应力之后，e-log(t)曲线变陡，蠕变速率增大，变形明显增大。而且，在这个过程中，次固结系数也在不断变化:在结构屈服应力之前，次固结系数随着荷载的增加而显著增大，在荷载大于结构屈服应力之后，次固结系数增加到最大值，之后缓慢减小，但结构屈服前的次固结系数远小于结构屈服后的。

图5 试样e－log(P)曲线

同一荷载下不同时间段内的次固结系数的变化与压缩曲线的形状相关，对于Ⅰ型压缩曲线，次固结系数随着荷载持续时间的延长而减小 (见表2);对于Ⅱ型的压缩曲线，在加载后一定时间内，次固结系数是逐渐增大的 (见表3);而对于Ⅲ型的压缩曲线，在加载后一定时间内，次固结系数是先增大后减小的 (见表4)。

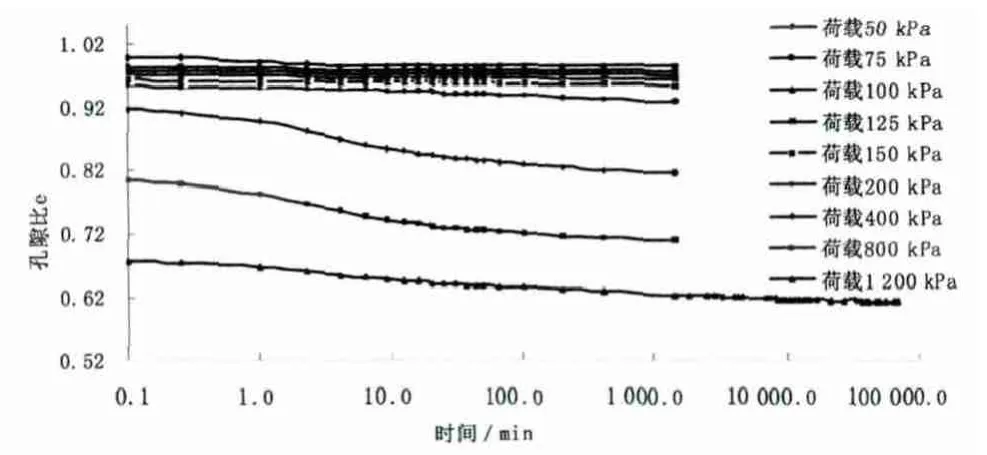
图6 试样zk5-8-4固结蠕变试验图

表2 土样zk5－8－7在500kPa下不同持续时间时的次固结系数表

表3 土样zk5－8－5在350kPa下不同持续时间时的次固结系数表

表4 土样zk5－8－6在400kPa下不同持续时间时的次固结系数表

5 压缩指数和次固结系数的关系

因次固结系数变化较复杂，故本文仅研究同一初始状态和相同荷载增量下，荷载持续某一固定时间内的次固结系数变化。

从图5可以看出，压缩指数 (e-log(P)曲线的斜率)随着压力的增大，值逐渐增大，这样的变化规律与次固结系数的变化规律极其相似。Mesri＆Godlewski(1977年)［3］总结了22种黏土的次固结试验结果指出，对于同一种原状土次固结系数与压缩指数的比值是一个常数，其值在0.025～0.100。经计算，本次试验次固结系数和压缩指数的比值在0.020～0.028，基本维持恒定，这与Mesri的结论是相符的。

6 应力历史对次固结系数的影响

为了研究应力历史对次固结的影响，试样zk5-8-5、zk5-8-6、zk5-8-7和zk5-8-8在施加到荷载300kPa之前的加载方式完全相同，在荷载300kPa下持续26d后，分别施50，100，200，500kPa等不同的荷载增量，试验成果见图1～4。由图1～4对比可知，4个试样在施加不同荷载前的变形规律完全相同，之后的变形就各有特色。

对比分析这几个图可知，试样在26d的持续荷载下，产生了明显的结构强度，使得变形状况与应力水平相关:在下一级荷载增量不大的情况下，变形曲线上主次固结的分界逐渐模糊，曲线几乎成了直线，次固结变形很小;随着荷载增量增加，主固结与次固结分界明显，次固结变形部分增大。此外，通过对次固结系数研究发现，在小荷载增量下，次固结系数前期 (24h内)较小，基本与原状土在超固结状态下的次固结系数 (也是24h内)相同，后期逐渐长大，但仍小于正常固结状态下的值 (约60%);在大荷载增量下，次固结系数基本不随时间变化，与原状土在正常固结下的值基本相同，不同荷载增量下次固结系数见表5。

对于试样zk5-8-5和zk5-8-6，在分别施加荷载增量50，100kPa荷载增量并持续12d后，再次分别加载250，50kPa，试验成果见图1和图2，可以看出，本次加载试样zk5-8-5的变形曲线出现明显的转折，次固结变形曲线与该土样在荷载300kPa下的变形曲线基本平行;而对土样zk5-8-6，因本次荷载持续时间短，不能产生足够的结构屈服应力，与试样zk5-8-5在荷载增量50kPa次固结相比，次固结变形明显小，次固结系数为0.00667，但小于该土样在荷载300kPa下正常固结状态时的值。

次固结变形是由于土骨架的流变蠕变作用产生的。上述试验表明，这类蠕变变形可以增加土的结构屈服应力，提高土体的抗变形能力，在一定荷载范围内可以大大减小土的次压缩性，但当荷载增大至某一值后，这种效应便会消失。

表5 不同荷载增量下次固结系数的变化表

7 结语

通过上述对固结过程中3个黏滞性效应的分析，可以得出以下结论:

(1)对于结构性土，次固结系数与应力水平密切相关，在固结荷载小于结构屈服应力时，次固结系数随着荷载的增加而显著增大，在荷载大于结构屈服应力之后，次固结系数增加到最大值之后缓慢减小，但结构屈服前的次固结系数远小于结构屈服后的。根据试验成果，海积软土在超固结阶段也有明显的次固结现象，在对这类土的工后沉降计算中须考虑这一因素。

(2)同一种原状土次固结系数与压缩指数的比值在较小的范围内变化，可以看作是一个常数;历史应力和加荷比对次固结变形都有很大的影响。

(3)次固结变形是由于土骨架的黏滞性蠕变作用产生的，这类蠕变变形可以增加土的结构屈服应力，提高土体的抗变形能力，在一定荷载范围内可以大大减小土的次压缩性，但当荷载增大至某一值后，这种效应便会消失。海堤一般都建在深厚的海相软土层上，工后沉降时间漫长，蠕变次固结沉降占的比例较大，据本文的试验成果，如采用合理的加载施工工艺，在一定程度上可以大幅减少工后沉降。

［1］ Bjerrum L. Engineering geology of Norwegian normally consolidation marine clays as related to the settlement of building［J］.Geotechnique，1967，17(12):81-118.

［2］ Crawford C B.State of the art:evaluation and interpretation of soil consolidation tests［C］ //Proc.ASTM Symp.consolidation behavior og soils.Fort Lauderdale，1985，STP892，PP:71-103.

［3］ MesriG，GodlewskiP M.Time and stresscompressibility interrelationship ［J］.ASCE Journal of Geotechnical Engineering Division，1977，103(GT5):1067-1070.

［4］ NagarajT S， Pandian N S， Narasimha Raju P S R.Compressibility behavior of soft cemented soil［J］.Geotechnique，1998，48(2):281-287.

［5］沈珠江.软土工程特性和软土地基设计［J］.岩体工程学报，1998，20(1):100-111.

［6］殷宗泽，张海波，朱俊高，等.软土的次固结 ［J］.岩土工程学报，2003，25(9):521-526.

［7］魏汝龙.软黏土的强度和变形［M］.北京:人民交通出版社，1987.