基于BP神经网络的义乌市降水量预测

吴 麟,冯利华

(浙江师范大学地理与环境科学学院,浙江 金华 321004)

1 问题的提出

随着人工神经网络自身技术的不断完善,应用人工神经网络成功解决各类地学问题的案例大量出现。在地学分析中使用的各类人工神经网络类型中,在水文、地质、大气、遥感等领域应用较为广泛[1]。在水文领域,神经网络技术的应用包括了降雨预报、径流预报、水质与水量预测、水库优化调度、地下水管理、水土资源利用规划等方面的研究,并且BP模型应用最广,占到85%以上[2]。

由于大气遥相关的存在,厄尔尼诺所形成的热带海洋热状况变化所造成的大气环流和气候变化将传播到中高纬度[3]。而NINO-3区涵盖了赤道东太平洋的大部分海域,其海温变化在厄尔尼诺和拉尼娜事件中具有很好的代表性。有研究表明NINO-3区水温的变化可导致次年春季副高和东亚大槽强度产生变化,进而影响我国气候[4]。

鉴于此,在经济快速发展与水荒矛盾日益激化的今天,拟用BP神经网络的方法,用NINO-3区海表温度作为预测因子对义乌市大气降水进行预测。以期为义乌市的开源节流工作提供参考,包括水库蓄水、人工增雨等。同时,也为其它地区的水资源预测提供方法上的借鉴。

2 方法与材料

2.1 BP神经网络

BP神经网络基于误差反向传递算法(Back-Propagation),其网络拓扑结构见图1[5]。

图1 神经网络拓扑结构示意图

在BP神经网络的构建中,所选用的传递函数是反映下层输入对上层节点刺激脉冲强度的函数,一般取(0,1)内连续取值的Sigmoid函数：

BP网络的输入层一般没有阈值和激活函数,即输入层神经元的输出等于输入神经元的输入,而隐含层和输出层神经元的输出则须经过权重和阈值的处理。设网络具有层,设输入层为第0层,令ymj表示第m层中第j个结点的输出,而yj0就等于xj,即第j个输入,令Wmij表示从第m-1层i节点到m层j节点的连接权,θmj表示第m层第j结点的阈值,BP神经网络训练步骤如下[6]：

(1)将各权值和阈值赋予间的随机数；

(2)从训练数据组中选一数据对(Xk,Tk),将输入变量加到输入层(m=0)使

式中：k表示训练图形号,即训练模式的序号。

(3)信号通过网络向前传播,即利用关系式：

计算从第1层开始的各层内每个结点j的输出ymi,直至全部完毕。其中F(x)取Sigmiod函数；

(4)计算输出层每个结点的误差变化率：

这个误差由实际输出值和目标要求值之差获得。

(5)计算前面各层每个结点的误差变化率：

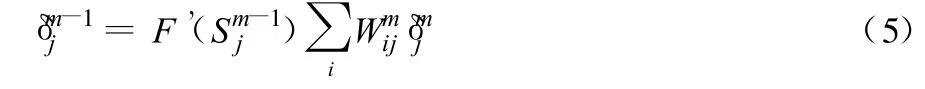
由逐层反传误差算得(m=m,m-1,…,1)。

(6)反向逐层修正权值和阈值：

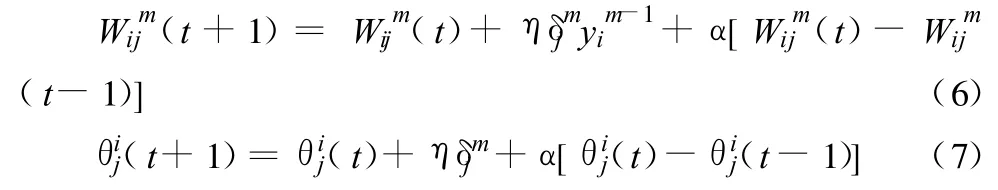
式中：t为迭代次数；η为学习速率[η∈(0,1)]；α为动量因子[α∈(0,1)]。η较大时,收敛快,但不稳定；η较小时,收敛慢；α正好与η相反。

(7)返回至步骤(2),转入下一个图形,重复步骤(2)～(7),直至网络全局误差：

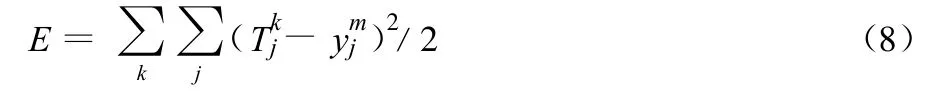
E达到预设的精度E0为止,即E≤E0。

神经网络训练好后,相应的网络结构和参数设置(权值和阈值等)就已确定,此时学习过程将自动结束,构建好的BP模型即可进行预报分析。

降水量预测是非线性问题,许多因变量与自变量之间的关系无法用具体的函数来描述,而BP神经网络技术模拟大脑的思维过程,具有非线性适应性信息处理能力,恰好避开这一难题[7]。通过神经元之间的相互作用完成整个网络的信息处理,根据对非线性函数的复合逼近输入和输出之间的映射,具有自学习、自组织和容错性等一系列优点,用它来进行降水量预测是可行的。

2.2 数据来源

义乌市全年降水时间分配不均,该区多年平均降水量为1406mm,其中主要集中在5—6月,2个月的降水占全年降水的31%。因此,本文中的预测对象采用5—6月的降水总量,原始数据来源于中国气象局国家气候中心。

使用前一年的11月、12月以及次年的1月、2月、3月、4月的任一单月NINO-3区月平均温度以及这6个月的任意组合,来预测义乌市次年5—6月的总降水量。经过多次的试预测,最终选出了误差最小的预测方法,即用前一年12月的NINO-3区海表平均温度来预测义乌市次年5—6月的总降水量预测效果最佳。因此,选用NINO-3区12月的海表平均温度作为预测因子(见表1)。

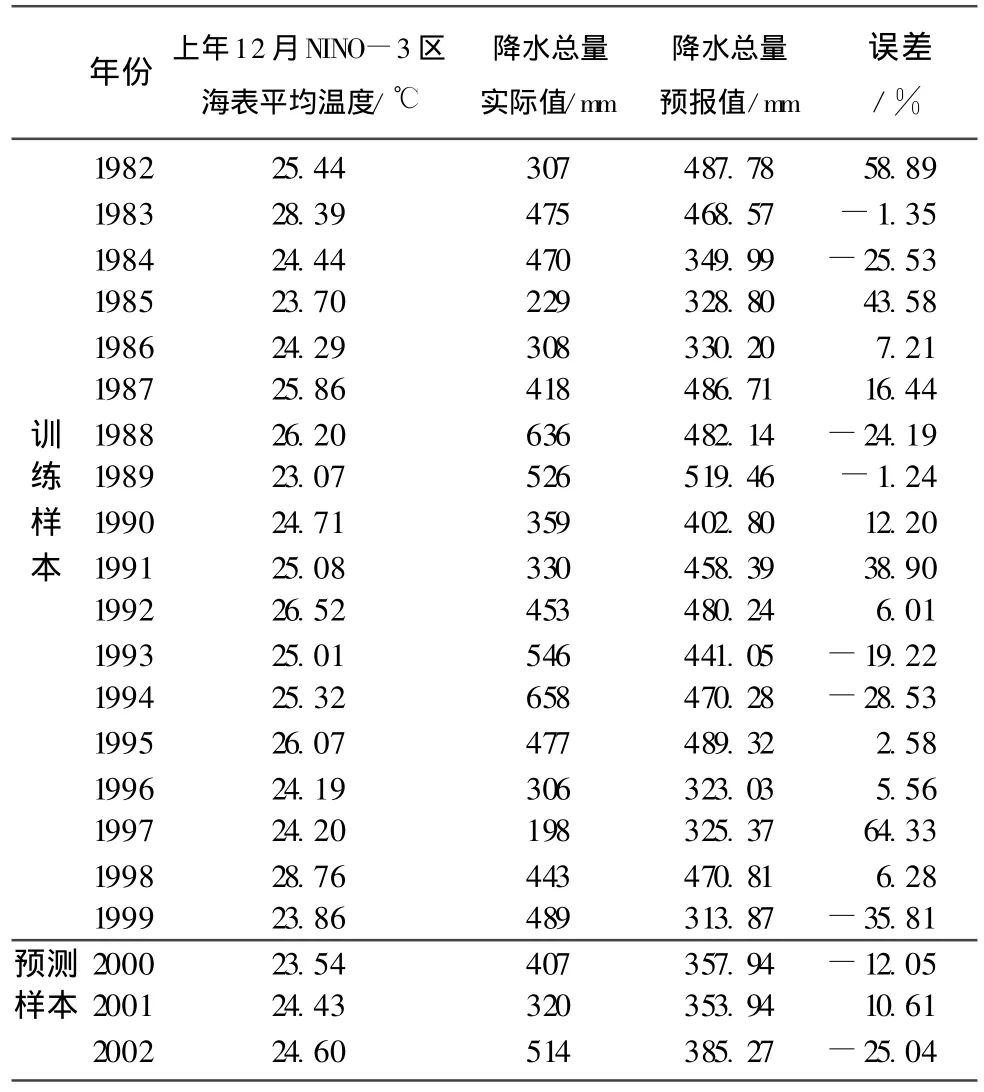
表1 12月NINO-3区海表平均温度以及义乌市5—6月降水总量及其预报结果表

3 网络训练过程及结果检验

1989 年 Robert Hecht和Nielson证明：在任何闭区间内一个连续函数都可以用一层隐含层的BP网络逼近,因而一个3层的BP网络可以完成任意的n维到m维的映射。为此本案例采用单隐含层的3层网络结构。1947年,Kolmogorov阐述了一个涉及隐含层节点数的内容,人们称之为Kolmogorov定理。此定理提及隐含层的节点数为2n+1个单元。由于输入层的节点数n=1,根据Kolmogorov定理,隐含层的节点数2n+1=3。由此得到用于降水预报的神经网络拓扑结构为 (1,3,1)。

将1981—1999年12月NINO-3区海表平均温度的数据作为网络训练样本,将数据加载到BP网络后,对网络进行训练和学习。选取学习率η=0.2,动量因子α=0.6,误差容限E0≤0.4,即预设精度为40%,训练次数为50万次。

将表1中2000—2002年义乌市5—6月降水量作为测试样本,对训练好的网络进行预报。由于训练过的网络已“模拟”并“记忆”了输入变量和输出变量之间的 “函数关系”,因而可以用它来进行义乌市5—6月降水总量的预报。网络测报结果列于表1,训练样本的平均误差为21.22%,预测样本的平均误差为15.90%,预报情况良好。

4 结 语

水资源已经极大地制约了义乌市的经济发展,降水量预测对义乌市的意义十分重大。然而,虽然在自然界许多因变量y与自变量x之间存在着密切的关系y=f(x),但这种关系无法用一个具体的函数来描述。正如NINO-3区海表温度以及义乌市降水量之间,无法建立具体的函数关系。而BP神经网络的最大优点在于它不需要设计任何数学模型,只要通过对历史数据的训练和学习,网络就能够“模拟”并“记忆”输入变量和输出变量之间的任何复杂的“函数”关系。

经过多次试预测,选出12月NINO-3区海表平均温度作为预测因子,义乌市5—6月的降水总量为预测对象。将1981—1999年12月NINO-3区海表平均温度的数据作为网络训练样本,2000—2002年义乌市5—6月的降水总量作为测试样本。网络测报结果平均误差为15.90%,预报情况良好。将神经网络预测方法用于降水量预测,不仅可以为义乌市的开源节流工作提供参考,也为其它地区的水资源预测提供借鉴。

[1]李双成,郑度.人工神经网络模型在地学研究中的应用进展[J].地球科学进展,2003(01)：68-76.

[2]胡铁松,袁鹏,丁晶.人工神经网络在水文水资源中的应用[J].水科学进展,1995(01)：76-82.

[3]王远超,陈明璐,黎玲,等.2009年盛夏广西大范围干旱成因初探 [J].安徽农业科学,2010,38(12)：42-44.

[4]胡桂芳,邹瑾,张璇.下半年Nino3区海表升温对东亚春季大气环流及山东春季降水的影响 [J].应用气象学报,2005,16(6)：773-778.

[5]HaganMT,Demuth HB,Beale M.Neural network design[M].New York：PWS Publishing Company,2002：6-14.

[6]冯利华.基于神经网络的洪水预报研究[J].自然灾害学报,2000(02)：45-48.

[7]付东王,王超,张倩,等.基于 BP神经网络模型预测区域需水量 [J].城市道桥与防洪,2011(04)：93-97.