降雨作用下不同库水位升降速率对某滑坡稳定性的影响

张少琴,向 玲,王 力(三峡大学三峡库区地质灾害教育部重点实验室,湖北 宜昌 443002)

1 问题的提出

非饱和土滑坡的稳定性与降雨及库水位升降有着密切的关系,三峡水库在正常蓄水运营后,大量的边坡体在库水位周期性变化范围内,实践表明,库水位周期性涨落对边坡稳定性的失稳有显著作用。例如：自1941年Rasevelt湖蓄水以来,49%的滑坡发生在库区蓄水初期,30%发生在水位骤降期；在日本约60%水库滑坡发生在库水位骤降期,而另外40%基本发生在水位上升期。国内外学者针对库水位升降所引起的边坡失稳问题做了大量的相关研究[1-5],罗红明(2008年)在对三峡库区赵树岭滑坡进行数值模拟计算后,得出库水位上升时滑坡稳定性系数有总体逐渐增大趋势,而库水位下降时滑坡稳定性总体逐步减小[3]。刘才华(2005年)认为在库水位上升过程中,边坡的稳定性有一个先降低后增加的过程[4]。梁学战(2012年)则分析了三峡库区库水位升降作用下不同渗透系数滑坡体浸润线的分布规律及滑坡稳定性变化规律[5]。以上研究均未从库水位升降速率考虑对滑坡稳定性影响。

本文以三峡库区秭归县某滑坡为研究对象,利用有限元计算软件,在三峡水库正常运营最危险工况基础上取不同库水位升降速率进行滑坡渗流计算,获得不同库水位升降速率下的地下水位,采用Morgenstern-Prince法,考虑库水位升降速率变化引起的地下水位变化,计算获得滑坡在不同库水位升降速率条件下的稳定系数。

2 饱和—非饱和渗流计算基本理论

浸润线是饱和土体与非饱和土体的分界线,库水位升降作用下滑坡体内地下水浸润线的变化属于饱和与非饱和问题,在库水位升降过程中,滑体内地下水浸润线也有规律的起伏,饱和土与非饱和土的作用面积随之发生变化,根据质量守恒及Darcy定律可得到二维的饱和与非饱和渗流控制方程：

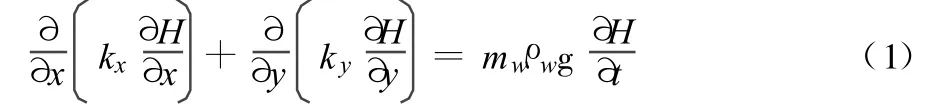
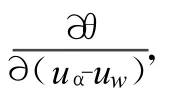
非饱和渗流问题的边界条件有多种形式,本文研究的问题是降雨作用下不同库水位变化速率引起的滑坡体内暂态渗流场浸润线的变化情况,边界条件主要包含定水头边界及定流量边界2类：

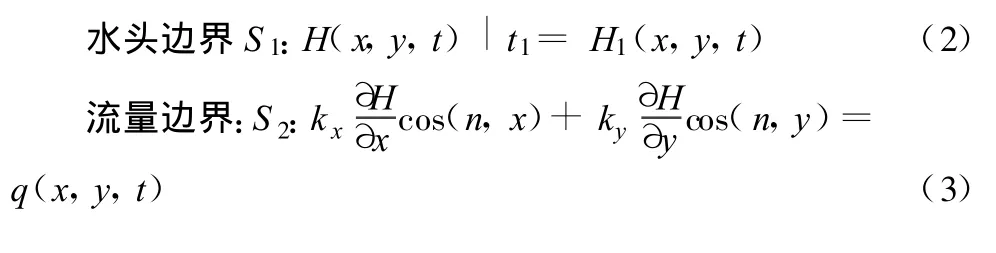
3 稳定性计算理论

涉水边坡稳定性分析不仅要考虑饱和区地下水压力变化影响,而且还应考虑非饱和区基质吸力变化影响,故采用Fredlund(1978年)提出的考虑了负空隙水压力的非饱和土抗剪强度公式(4)：

式中,φ''为随吸力变化的内摩擦角 (°)。相较Bishop的理论公式,式(4)强调了负孔隙水压力对非饱和抗剪强度的影响,且式(4)参数确定较容易,目前得到岩土界的广泛认可。

本例中用Morgenstern-Price法在考虑基质吸力情况下计算不同速率库水位升降作用滑坡的稳定性变化。运用Geostudio软件,将在Seep/W模块模拟二维稳态和瞬态的饱和—非饱和渗流有限元计算进行渗流场分析,再将分析结果导入Slope/W模块中,进行稳定性分析。该程序需输入的已知条件包括滑坡剖面、各地层的土水特征曲线、各地层非饱和渗透函数和水头降雨等边界条件。

4 考虑不同工况的模拟分析

4.1 计算模型

模拟计算以三峡库区秭归县某滑坡作为计算对象,根据该滑坡地质勘察报告及物探资料,滑动面选择滑带土中某一光滑层面。滑坡计算模型见图1,网格采用四边形网格,共有节点7839个,7715个单元,计算方法为考虑基质吸力的Morgenstern-Price法。

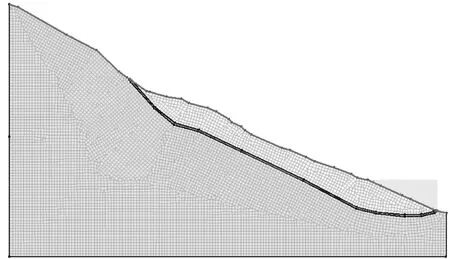
图1 滑坡计算模型图

4.2 边界及材料条件

根据三峡库区秭归县某滑坡地质勘察报告关于岩土体的物理力学参数建议值和反演获得的滑体凝聚力和摩擦角,类比三峡库区其它类似滑坡岩土体的物理力学性质参数值,综合确定该滑坡二维有限元数值计算参数,该滑坡滑体及滑带的土水特征曲线及渗透函数曲线见图2、3,其他物理力学参数值见表1。

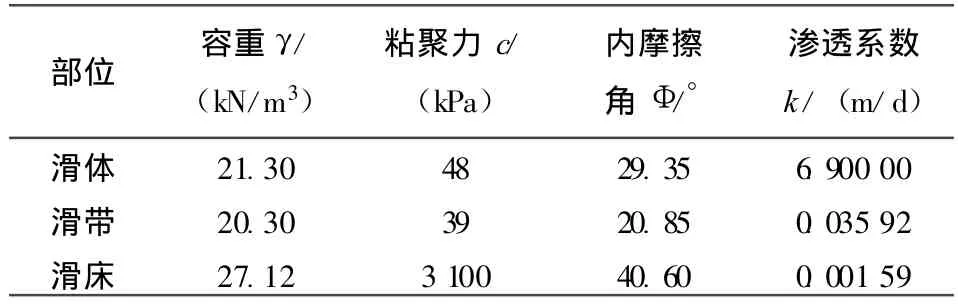
表1 滑坡计算参数表

滑坡在降雨和水库水位变化条件下渗流的边界条件描述如下：

水头边界：该斜坡前缘被库水浸没部分为水头边界。

流量边界：斜坡表面处取降雨引起入渗的流量边界,当降雨强度大于坡面岩土体的入渗速度时,取岩土体的入渗速度值作为边界流量值；当降雨强度小于坡面岩土体的入渗速度时,取降雨强度值作为边界流量值,取降雨强度计算。

两侧和底部渗流边界：模型底面和两侧为自由渗流边界,在此由于基岩的渗透性很小,可认为是不透水边界。

图2 滑体土土水特征曲线及渗透函数曲线图

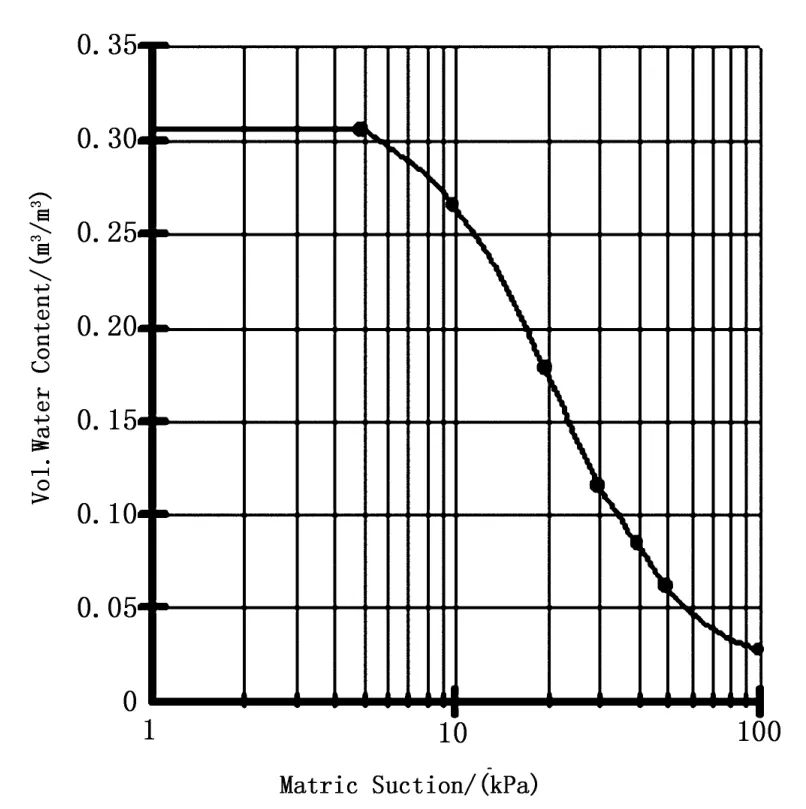
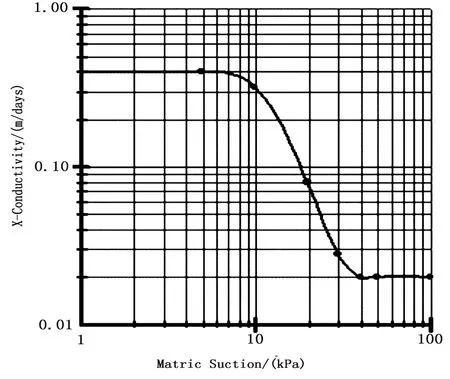
图3 滑带土土水特征曲线及渗透函数曲线图

4.3 计算工况

三峡库周期性运营状况直接影响库区滑坡的渗流场变化,本文按照三峡水库蓄水后正常运营时的水位调节方案,分为如下3个工况(见表2)：

表2 计算工况及荷载组合表

4.4 渗流模拟结果

采用饱和—非饱和非恒定渗流理论计算滑坡在各工况下滑坡体内的地下水位和孔隙水压力的变化基本与库水位变动同步(见图4)。由图4(a)、(b)可见,水位下降时地下水位下降稍滞后与库水位,表现出指向坡外的渗透压力。由图4(c)可以看出,随着库水位上升,滑坡体内地下水位现明显滞后于库水位上升,地下水出现“倒流” 现象,表现出指向坡内的渗透压力。

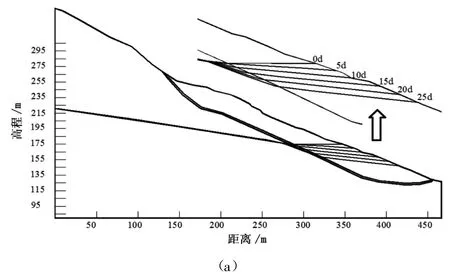
图4 滑坡在各工况下地下水位变化示意图

4.5 稳定性计算

通过考虑饱和—非饱和渗流场与应力场耦合的有限元法,计算库水变动工况下叠加50a一遇强度降雨时的该滑坡稳定性变化情况。不同库水位变动叠加降雨时该滑坡安全系数变化曲线见图5。可以看出,在3d 50a一遇强度的降雨作用下,库水位由175.0m下降至145.0m(下降速率1.0m/d)库水向坡体外渗流产生向内渗透力,坡体安全系数均显现不同幅度的下降,从175.0m初始时刻的1.111下降为1.050。而库水位由162.0下降至145.0m(下降速率2.0m/d)过程中,坡体安全系数由1.088下降到1.044,且下降趋势明显。库水位由145.0m上升到175.0m的水位上升过程中,库水向坡体内渗流产生向内渗透力,降雨作用下,安全系数由1.091上升到1.141。

5 考虑不同库水位升降速率的模拟分析

根据第3节滑坡二维稳定性分析结果,该滑坡最危险工况为工况a(库水位从162.0m水位骤降至145.0m+50a一遇暴雨),在该工况条件下,滑坡的稳定系数最小值为1.044,滑坡处于欠稳定状态。

取不同库水位升降速率 (以最危险工况下的库水位下降速率2.0m/d为初始值逐渐增加)进行滑坡渗流计算,获得不同库水位升降速率下的地下水位,采用Morgenstern-Prince法,考虑库水位升降速率变化引起的地下水位变化,计算获得滑坡在不同降雨条件下的稳定系数,计算结果见图6。由图6可见,水位下降速率增大的初始阶段,安全系数出现一个明显的陡降过程,而大于3.0m/d的水位降幅后,安全系数减小速度变缓。在50a一遇降雨作用下,当库水位下降速率达到8.0m/d时,滑坡安全系数小于1.000,处于失稳状态。

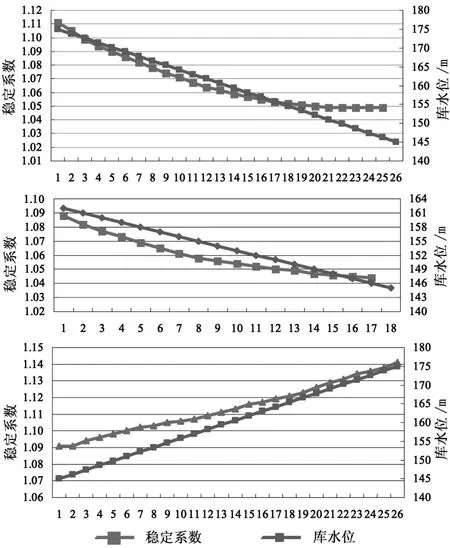
图5 稳定系数随库水位升降变化曲线图

图6 不同库水升降速率下滑坡稳定系数变化图

6 结 语

(1)在暴雨作用下,随着库水位上升,稳定系数逐渐增大；随着库水位下降,稳定系数逐渐下降,滑坡受动水压力作用明显。

(2)随着库水下降速率的增大,滑坡的稳定系数逐渐减小,且在速率变化的初期阶段,稳定系数出现明显的陡降。在库水位达到3.0m/d后,速率变化导致安全系数减小的幅度逐步减缓。

(3)在该库水位运行最危险工况下,升降速率由2.0m/d增加到极限值8.0m/d时,稳定系数小于1.000,该滑坡处于失稳状态。

[1] Lane P A,Griffiths D V.Assessment of stability of slopes under drawdown conditions[J].Journal of Geotechnical and Geoenvironmental Engineering,2000,126(5)：443-450.

[2]王力.降雨作用下不同渗透性系数对滑坡稳定性的影响[J].浙江水利科技,2013(4)：1-6.

[3]罗红明,唐辉明,章广成,等.库水位涨落对库岸滑坡稳定性的影响 [J].地球科学—中国地质大学学报,2008,33(5)：687-692.

[4]刘才华,陈从新,冯夏庭.库水位上升诱发边坡失稳机理研究[J].岩土力学,2005,26(5)：769-773.

[5]梁学战,陈洪凯.库水位升降条件下不同渗透性的滑坡体稳定性变化规律[J]中国地质灾害与防治学报,2012,23(4)：20-26.

[6]王力,王世梅,杨贝贝.库水位变动条件下水—土特征曲线对滑坡稳定性计算结果的影响研究[J].三峡大学学：自然科学版,2012,34(3)：10-14.