基于蒙特卡罗方法的小卫星偏心分离动力学分析
2014-12-31沈晓凤肖余之杜三虎
沈晓凤,肖余之,杜三虎,张 华
(1.上海市空间飞行器机构重点实验室,上海 201109;2.上海宇航系统工程研究所,上海 201109;3.上海航天技术研究院 空间安全与维护总体技术研究中心,上海 201109)
0 引言
1961年苏联航天员手动在轨释放了顶点侦查卫星,并成功对美国本土进行了拍摄,这是小卫星在轨分离技术的首次应用。随着小卫星技术以及空间站的迅速发展,利用机动平台(上面级)在轨释放与在轨部署小卫星作为一种更经济的方式受到青睐。由于多星释放,必然存在偏心安装,因此必须对小卫星偏心分离动力学进行研究。
国内对在轨分离小卫星技术进行了研究。文献[1]考虑近地轨道摄动力影响,基于HILL方程对小卫星的分离速度进行了分析和推导;文献[2]对采用弹簧推杆式分离机构的空间飞行器的对接分离过程进行研究,并由地面试验结果得到较好的验证;文献[3]类比平移副约束的分离问题,对筒式偏心在轨分离小卫星展开动力学分析;文献[4]对多星二次分离展开研究,对同时释放和依次释放各子星的影响因素进行了探讨。上述研究多侧重于小卫星分离过程的动力学分析,对其分离机构、分离性能的优化和可靠性分析尚未全面展开。
由于小卫星和分离平台间安装和连接方式的多样性,不同的简化模型和初始状态对分离过程和最终精度的影响较大,有时候甚至是决定性的。研究其中的主要因素并分析其影响规律,对偏心在轨分离小卫星的研究具有重大的指导意义。本文对基于蒙特卡罗方法的小卫星偏心分离动力学进行了研究。
1 偏心在轨分离模型
设小卫星分离前安装在释放筒内部,底部作用分离弹簧,释放筒偏心安装在主平台上,其相对主平台的安装位置和坐标系定义如图1所示。小卫星上分别设置了三个上支撑和三个下支撑与释放筒上的三根导轨配合,上下支撑内部均装有压紧弹簧,与导轨间的压力可根据需要进行调节,三方向设置如图2所示。
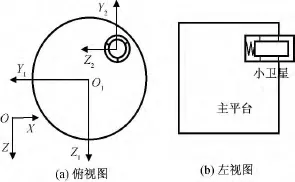
图1 偏心在轨分离模型Fig.1 Eccentric sub-satellite model
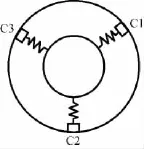
图2 三方向支撑分布Fig.2 Supporter distribution
下支撑出筒后,小卫星无外力作用,其分离姿态已确定,故定义其出筒时刻为下支撑出筒时刻。
2 分离动力学仿真
建立如图1所示的坐标系,其中O-XYZ为轨道惯性坐标系,o1-x1y1z1为主平台本体坐标系,o2-x2y2z2为小卫星本体坐标系。建立分离动力学模型时,采用以下假设:
a)小卫星为刚体,并将释放筒与主平台视为同一刚体,分离过程可考虑为两刚体运动过程。
b)将支撑活塞与导轨两者间的接触关系简化为非线性弹簧阻尼模型[5-6]。
c)分析所得的转动角度及转动角速度均为相对分离时刻的瞬时轨道坐标系。
d)在真空零重力条件下进行分离过程数学建模,不考虑摄动力影响[3]。
2.1 分离动力学理论
为避免奇异点的出现,在数学模型推导过程中采用3-1-2坐标转换顺序,把握分离过程中各矢量的关系,对小卫星与主平台进行受力分析。


数学模型推导中,重点是接触位移和接触力的建模,上支撑与导轨的接触力可表示为

式中:F′ui为各支撑坐标系中的接触力;F′uix,F′uiy,F′uiz分别为三方向接触力,Kc为等效接触刚度;μc为阻尼系数;Fn为初始预紧力;Arci为各支撑坐标系至轨道惯性坐标系的坐标转换矩阵。下支撑与导轨的接触力表示类同。
建立牛顿欧拉方程,通过四阶龙格库塔法求解可得小卫星与主平台的分离姿态[7]。有

式中:Ω24×24为状态矩阵;ri分别为惯性坐标系中的平台和小卫星质心位置;φi,θi,ψi分别为偏航、滚转和俯仰角,且Θi=[φiθiψi]T;ωix,ωiy,ωiz分别为平台在小卫星本体坐标系中的角速度,且ωi=[ωixωiyωiz]T;符号~表示反对称矩阵;

Ji为平台和小卫星的惯量张量而非单纯物理上的转动惯量[8]。其对角元素为刚体的惯量矩,非对角元素为刚体的惯量积,

2.2 ADAMS分离动力学仿真
ADAMS软件提供了参数化建模平台,可参数化定义几何尺寸、位置、力以及自定义函数等。分离动力学建模时,需对小卫星与主平台进行参数化处理,以便后续优化。
初步建模分析,由于偏心影响,导致三个下支撑出筒时刻不一致,下支撑预紧力越大,小卫星出筒时刻角速度突变越大。后续仿真分析中,设上支撑预紧力200N,下支撑预紧力为0N,分离弹簧行程200mm,分离力过质心,质量特性为
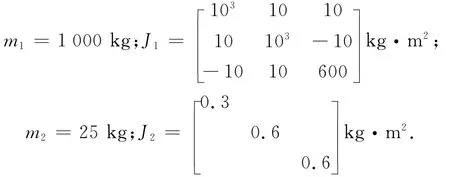
2.3 分离结果分析比较
基于Matlab平台利用数值算法得分离动力学理论结果,与ADAMS仿真结果曲线比较,结果如图3~5所示。由图可知:ADAMS仿真模型与数学模型的出筒姿态两者最大误差<0.15%,见表1。数学模型分析结果较好地验证了ADAMS的计算结果,说明后续利用ADAMS模型对小卫星偏心分离过程进行优化分析是可行的。

图3 小卫星三轴角速度Fig.3 Satellite’s angular velocity
2.4 分离过程力学现象与机理
分离过程中的力学现象为:在上支撑出筒前,小卫星跟随主平台运动;上支撑出筒以后,小卫星三轴角速度反向增加,主平台的三轴角速度基本维持不变。

图4 小卫星三轴速度Fig.4 Satellite’s velocity

图5 上支撑C2向接触力Fig.5 Contact force on C2supporter
分离过程机理是:偏心分离过程可看成类似平动与转动牵连运动的组合运动过程。图中:A处分离弹簧作用结束;B处上支撑出筒;C处下支撑出筒。整个分离过程可简单划分为三个工作时段(如图6所示):分离弹簧作用行程;上支撑作用行程;下支撑作用行程。小卫星质心介于上下支撑间,当小卫星的上下支撑与释放筒上的导轨同时作用,可近似等效为小卫星与释放筒间为平动副作用,小卫星与主平台有相同的角速度;上支撑出筒后,单独在下支撑作用下,根据转动牵连运动原理将使小卫星产生一个与主平台方向相反的角加速度(科氏加速度),小卫星的角速度反向增长。

表1 ADAMS仿真与理论结果Tab.1 Simulation results of ADAMS and theory

图6 小卫星与主平台分离角速度Fig.6 Angular velocity of satellite and platform
3 设计空间探索
设计空间探索,是从众多设计变量中找出对目标函数影响较大的设计变量及其组合方式,确定这些设计变量的初值,并估计出可能取得的目标函数值。设计空间的探索方法主要有近似建模、试验设计、鲁棒性设计、经典最优化方法和全局最优化方法等。
基于ADAMS仿真模型,考虑实际产品中可能出现推力偏斜、主平台与小卫星的惯量偏差、小卫星质心偏移等因素,把握设计变量与目标函数的变化关系,对其分离动力学性能进行优化,并提出优化措施。
3.1 试验设计
在进行蒙特卡罗分析前,先对各设计变量进行单因素多水平的试验设计,暂不考虑其他因素的耦合影响。
试验设计的变量主要有支撑弹簧预紧力、弹簧刚度、分离弹簧刚度等。设上支撑预紧力为0~450N,考虑三方向预紧力不均匀度,上支撑预紧力(100±10)N;下支撑预紧力0~10N,支撑弹簧刚度5~50N/mm,分离弹簧刚度在4.2~4.6N/mm范围内波动。设计目标为小卫星分离角速度和分离速度(合值)。
由目标函数的变化幅值,可得关键设计变量有上支撑预紧力、分离弹簧刚度和支撑预紧力的不均匀度。试验设计结果:
a)分离角速度、分离速度随上支撑预紧力的增加而降低;
b)考虑上支撑预紧力的不均匀性,随任一方向预紧力的增大,分离角速度降低,分离速度降低,C1向支撑预紧力对降低分离角速度最敏感;
c)支撑弹簧刚度对分离角速度、分离速度基本无影响;
d)预紧力一致,分离角速度、分离速度随分离弹簧刚度的增大而减小。
3.2 蒙特卡罗分析
设小卫星分离性能的主要因素及偏差值为:主平台质心偏差,本体坐标系{ΔX,ΔY,ΔZ}=±30mm;主平台惯量偏差±15%;小卫星质心偏差,本体坐标系{ΔX,ΔY,ΔZ}=±5mm;小卫星惯量偏差±10%;分离弹簧推力偏斜±0.2°;三个下支撑压力0~10N;三个上辅助压力(200±10)N;分离弹簧刚度4.2~4.6N/mm。基于ADAMS参数化仿真模型,用蒙特卡罗法对分离动力学过程进行可靠性与鲁棒性分析,得到在偏差范围内的目标最大值和概率分布。考虑初始偏差为正态分布,观察偏心分离后的分离角速度与分离速度的概率分布。输出结果分布如图7所示,数值见表2。

图7 初始设计下分离姿态概率分布Fig.7 Probability distribution of release attitude at initial iuput

表2 蒙特卡罗分析结果Tab.2 Results of Monte-Carlo method
基于蒙特卡罗分析结果,可生成输入参数及其组合对目标函数的敏感度分布。
前十阶敏感度最高的参数组合如图8、9所示。可知各参数对角速度影响的敏感度量级差别不大,其中右侧为正作用,左侧为反作用;影响分离速度的主要因素为分离弹簧刚度以及上下支撑预紧力,其中分离弹簧刚度贡献量最大(26%)。
4 分离动力学性能优化措施
基于上述仿真结果与设计空间探索的结论,提出优化措施,优化的目的是在保证足够大分离速度的前提下(暂取2.0m/s),尽可能降低小卫星的分离角速度。
a)方案一:缩短下支撑行程。

图8 各参数的分离角速度敏感度Fig.8 Sensitivity distribution of parameters on release angular velocity

图9 各参数的分离速度敏感度Fig.9 Sensitivity distribution of parameters on release velocity
根据分离过程的力学现象与机理可知,在单独下支撑作用下,小卫星角速度反向增大;在单独上支撑作用下,小卫星角速度同向增大,可得不等式分离弹簧作用行程≤上支撑作用行程≤下支撑的作用行程成立。
满足不等式,适当缩短下支撑行程,不改变分离速度,使小卫星提前出筒,即将图6中C点作用时间提前,可有效降低分离角速度。具体措施包括上移下支撑位置、改变导轨截面设置等。
b)方案二:同步提高上支撑弹簧预紧力。
根据试验设计已知分离角速度、分离速度随上支撑预紧力的增大而减小。提高上支撑预紧力至300N,将表2的参数输入进行蒙特卡罗分析,结果见表3,其分离角速度落在3σ内的最大值为3.266(°)/s,明 显 小 于 200N 预 紧 力 时 的3.484(°)/s。
c)方案三:仅提高C1向上支撑弹簧预紧力。
提高C1向上支撑预紧力,分离过程中,对小卫星施加与主平台反向的角加速度,降低了分离角速度。C1向上支撑预紧力分别为200,300,400,500N下的分离角速度如图10所示。由图可知:当C1向上支撑预紧力增大时,分离角速度降低。提高C1向上支撑预紧力至400N,将表2的参数输入进行蒙特卡罗分析,结果见表4。

表3 蒙特卡罗分析结果Tab.3 Results of Monte Carlo method
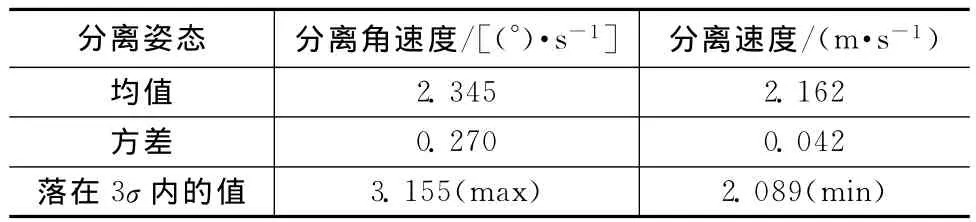
表4 蒙特卡罗分析结果Tab.4 Results of Monte Carlo method

图10 不同C1向上支撑预紧力的分离角速度Fig.10 Angular velocity with different preload on C1supporter
比较仅提高C1向预紧力至400N和同步提高三向预紧力至300N的优化效果,提高C1向预紧力能更有效地降低分离角速度。
除上述优化方法外,提高分离弹簧刚度等亦可有效降低分离角速度,但都需权衡速度与角速度的关系。
5 结束语
本文对偏心安装在主平台上的小卫星分离释放过程的动力学进行了研究,并进行设计空间探索与可靠性分析,优化分离装置,使其得以有效偏心分离。研究表明:基于多体动力学理论与ADAMS的计算结果基本一致,可用ADAMS分析此类小卫星偏心分离;考虑加工误差,以提高分离性能的鲁棒性,对仿真模型进行蒙特卡罗分析,可作为工程设计的可靠性分析;分离弹簧刚度以及上下支撑预紧力对出筒姿态最敏感,提高分离弹簧刚度和上支撑预紧力可有效降低分离角速度,但须权衡对分离速度的影响;在改动最少的前提下,仅提高C1向上支撑预紧力至400N对降低分离角速度最有效。
[1] 王功波,郗晓宁.小卫星在轨安全分离速度设计[J].中国空间科学技术,2007,27(3):33-38.
[2] 张 华,肖余之,徐博侯,等.空间飞行器的对接分离与地面模拟试验的仿真分析研究[J].宇航学报,2008,29(6):1761-1765.
[3] 蒋 超,王兆魁,范 丽,等.卫星筒式偏心在轨分离动力学分析[J].飞行力学,2010,28(1):76-79.
[4] 王秋梅,孟宪红.小卫星二次分离的动力学仿真[J].力学与实践,2009,31(3):23-26.
[5] 董富祥,洪嘉振.多体系统动力学碰撞问题研究综述[J].力学进展,2009,39(3):352-359.
[6] LEE T W,WANG A C.On the dynamics of intermittent-motion mechanisms,part 1:dynamics model and response[J].ASME Journal of Mechanisms,Transmissions and Automation in Design,1983,105:534-540.
[7] 章为仁.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998.
[8] 洪嘉振.计算多体系统动力学[M].北京:高等教育出版社,2002.
