基于迭代容积滤波的无源跟踪算法

章 静，王社阳，魏喜庆

（1.上海航天技术研究院，上海 201109；2.上海机电工程研究所，上海 201109）

0 引言

导弹对目标的跟踪时，传统主动雷达制导方法易受敌方电子干扰，当应用红外等被动传感器对目标进行跟踪，可较好地解决抗干扰问题。随着被动测量技术在跟踪和制导中的广泛应用，在仅有角度和距离的无源测量条件下对目标的状态进行估计引起了广泛关注。数学上，可在直角坐标系中用一个线性动态模型和一个非线性观测模型描述该问题，也可在极坐标系中用一个非线性动态模型和一个线性观测模型描述［1－4］。被动传感器获取目标的方位角和距离信息，当跟踪坐标系为直角坐标系时，因测量方程为非线性，故无法直接采用线性滤波方法。一种最直接的方法是将非线性模型进行近似线性化，对线性化的系统采用卡尔曼滤波框架，即扩展卡尔曼滤波（EKF）［5］。但经一阶线性化近似后，EKF忽略了模型部分非线性特性，当初始误差较大时，存在估计效果急剧下降和滤波收敛速度缓慢的问题。为进一步改善非线性系统估计性能，文献［6］根据对随机变量的概率分布进行逼近较对非线性函数进行逼近更容易的方法，提出了无迹卡尔曼滤波（UKF）［6］。UKF通过经无迹变换后的采样点集逼近非线性函数概率分布，并继承了卡尔曼滤波框架，其非线性估计性能优于EKF。UKF无需计算非线性系统的雅可比矩阵，因其良好适应性受到了广泛关注。用高斯埃尔米特积分公式得到的高斯埃尔米特滤波器，具有较UKF更好的估计精度和数值稳定性，但其计算量随状态维数增加而呈指数级增长，庞大的运算量导致其只能适于低维系统。文献［7］通过三阶容积法则的数值积分方法，近似高斯加权积分推导出了容积滤波（CKF），认为CKF是UKF在特殊参数选取情形下的一个特例，但具有更好的滤波精度和数值稳定性。

为此，本文提出了一种二维目标的相对状态估计算法。

1 纯方位测量问题描述

本文研究在二维平面内对目标的无源跟踪，数学表达式为

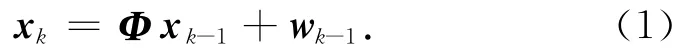
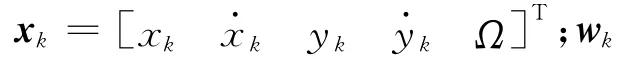
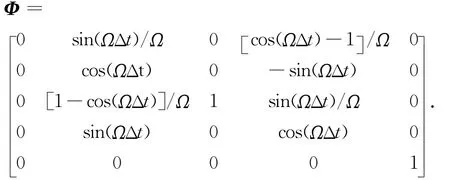
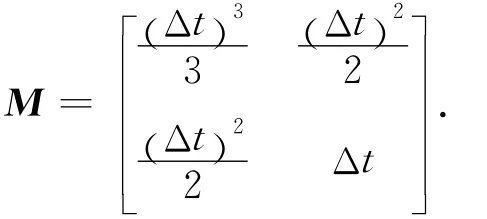
假设观测雷达位于坐标原点，则观测值信息

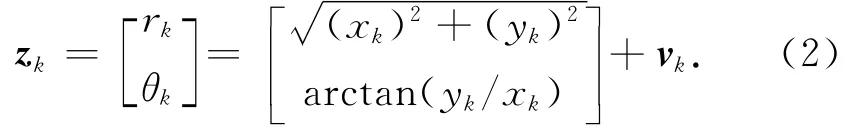
式中：xk，θk分别为距离和角度测量值，vk∈N（0，Rk）为测量噪声。该测量模型具有典型的非线性特性［8］。

2 容积滤波

具加性噪声的非线性系统状态方程和量测方程可表示为

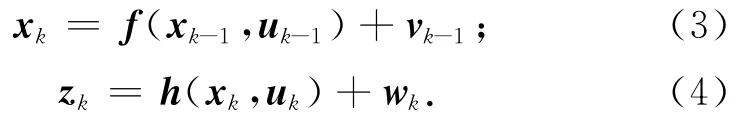
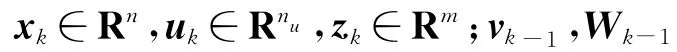
非线性高斯滤波的核心是求解多变量非线性函数与高斯密度函数乘积的积分。文献［7］通过三阶容积积分法则，利用2n个容积点加权求和替代加权高斯积分。对函数f（x）的加权高斯积分

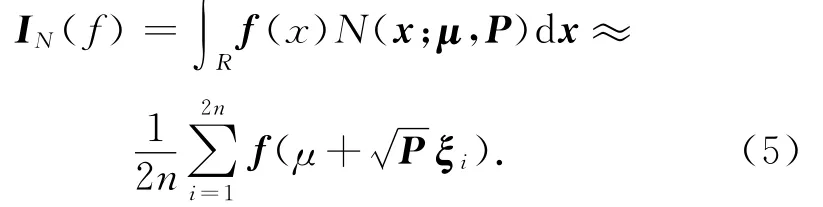
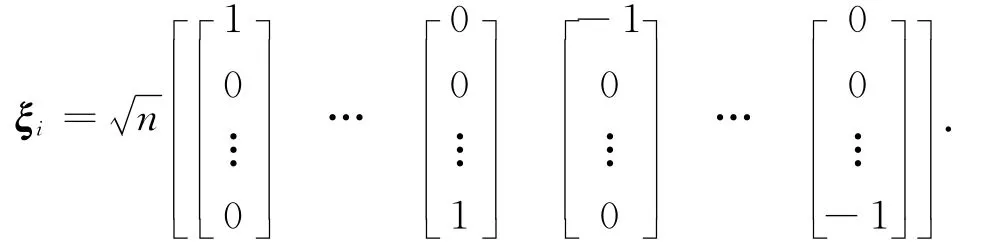
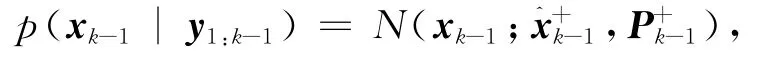
a）时间预测

计算容积点

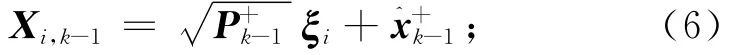
容积点传播

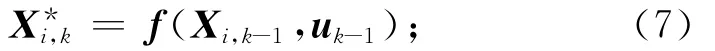
估计预测均值和协方差阵

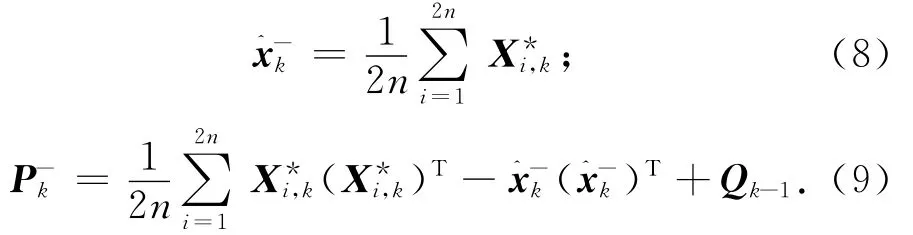
式中：i＝1，…，2n。

b）量测更新

计算容积点

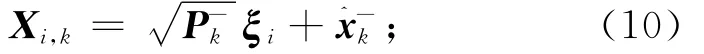
容积点传播

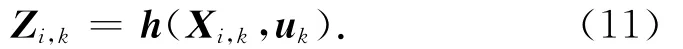
c）量测预测值、新息方差和协方差矩阵计算

d）计算量测更新

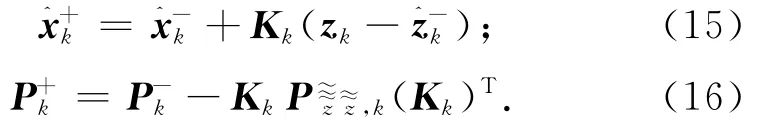
3 迭代容积滤波

无源测量模型具强非线性特性，为获得良好的滤波效果，本文用LM算法改进CKF的量测更新过程。与加权最小二乘算法类似，定义时刻k的代价函数

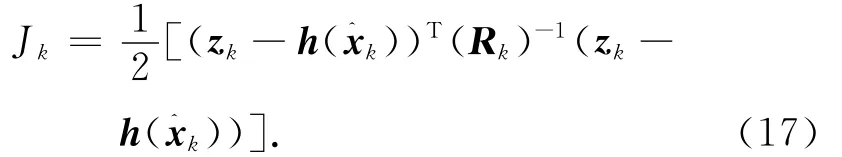
式中：为状态估值。设时刻k第j步的状态迭代预测值已知，则未知状态与当前状态和修正值Δxk，j的关系可表示为

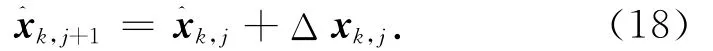
定义第j步迭代估计时的残差值

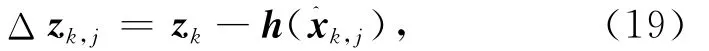
第j＋1步迭代的残差值

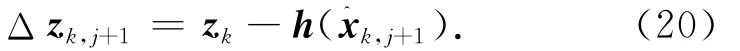
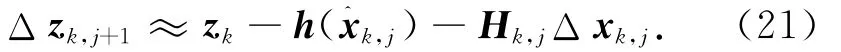
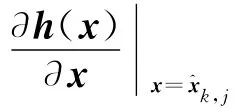
将式（22）代入式（17），代价函数变为

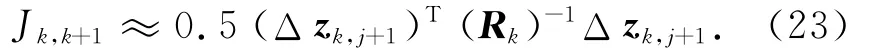
确定修正估计值Δxk，j的原则是其满足代价函数Jk，j＋1最小。最小化Jk，j＋1的问题与求解加权最小二乘问题等价，易求得

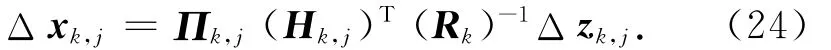
式中：Πk，j为方差阵，且Πk，j＝ （（Hk，j）T（Rk）－1＋ηIn×n）－1。此处：η为加权系数；In×n为n维单位阵。当η趋于0时，式（24）等价于高斯最小二乘微分修正算法（GLSDC）；当η趋于无穷时，式（24）等价于最速下降法。

LM算法克服了高斯最小二乘微分修正算法在先验估值与真值相差较大时收敛速度较慢的不足，以及在估值接近最优值时最速下降法收敛速度变慢的缺点。基于LM算法的改进CKF算法在进一步提高了CKF估计精度的同时，具有较快的收敛速度。将状态量测更新过程用LM算法替代为

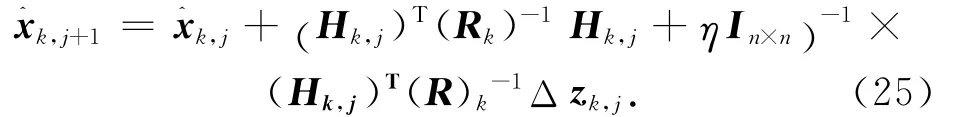
式中：取为计算得到的预测状态值。由于线性系统的互协方差阵的值为

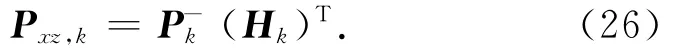
代入式（25）

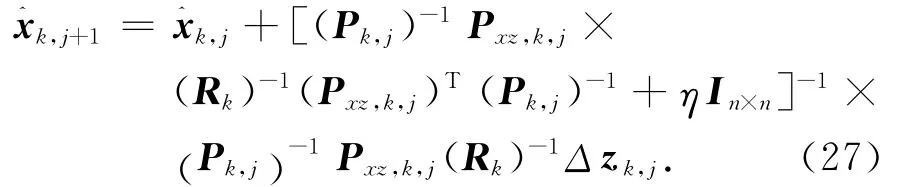
定义伪测量矩阵

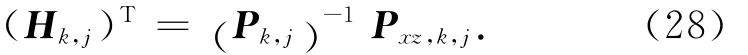
式中：Pk，0＝Pk；Pxz，k，j＝Pxz，k［14］。则状态量测更新

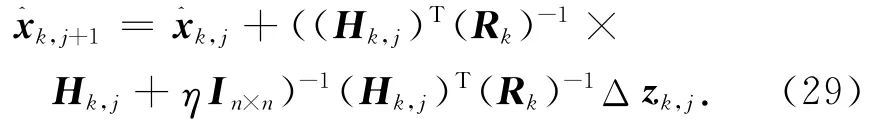
定义迭代卡尔曼增益

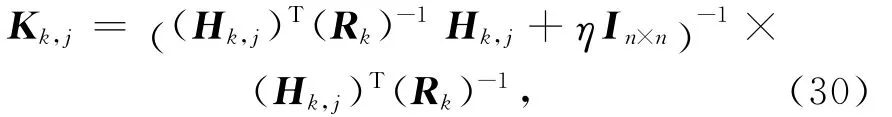
则式（29）可简化为

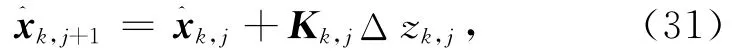
协方差矩阵

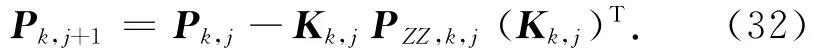
当代价函数Jk，j随迭代次数的增加而变化较小时，满足迭代终止条件

按以下准则选取LM算法中的η：η初值取一个较大的值（通常取 （Hk，j）T（Rk）－1Hk，j范数10倍以上）。将式（31）迭代计算的状态估计值代入式（23）中，若Jk，j＋1≥Jk，j，则舍去这次的状态迭代值并将η变为5η；若Jk，j＋1＜Jk，j，则保留状态估计值并将η变为η／5。

适当选取式（33）迭代终止条件的系数ε，本算法能在达到良好估计精度时及时跳出迭代，一定程度保证了算法的实时性。

4 迭代容积滤波在无源跟踪中应用

目标进行无源跟踪仿真时，设仿真步长Δt为1s；Rk＝diag［100m210rad2］；仿真时长T＝100s；状态初值及其估值分别为

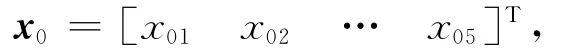
x1＝ ［0m 0m／s 0.4m －0.05m／s 0rad］T，相应的协方差阵P0对角线元素分别为100m2，10m2／s2，100mrad2／s2。此处：x01＝0.05m；x02＝0.01m／s；x03＝0.7m；x04＝－0.055m／s；x05＝0rad。定义横向位置均方根误差γpx、纵向位置均方根误差γpy、位置均方根误差γpos、速度均方根误差γvel和角速度均方根误差γtum－rate分别为

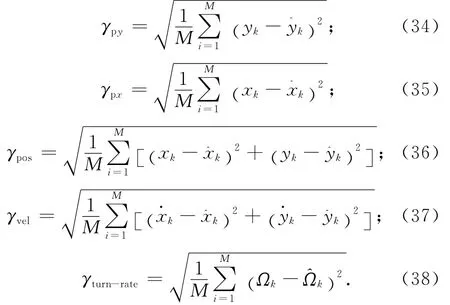
进行了100次蒙特卡洛仿真，目标的跟踪轨迹与真实飞行轨迹如图1所示。由图可知：因测量信息较少导致EKF的精度较低，在时间大于50s后出现了严重的滤波发散；UKF，CKF的估计精度较高，估计曲线与真实轨迹几乎重合。因EKF估计结果发散，UKF，CKF的均方根误差分别如图2～4所示。由图可知：CKF，UKF的速度和角速度估计精度非常相似，CKF的位置估计精度略优于UKF。

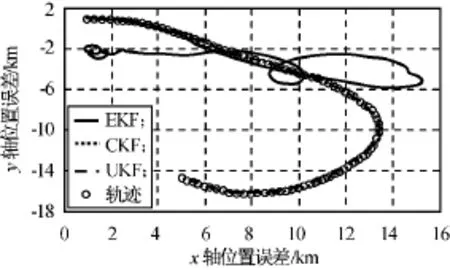
图1 飞行轨迹Fig.1 RMSE trajectory

位置、速度与角速度的RTAMSE值见表1。由表可知：CKF的精度略高于UKF，而EKF的跟踪结果发散，无法实现有效。

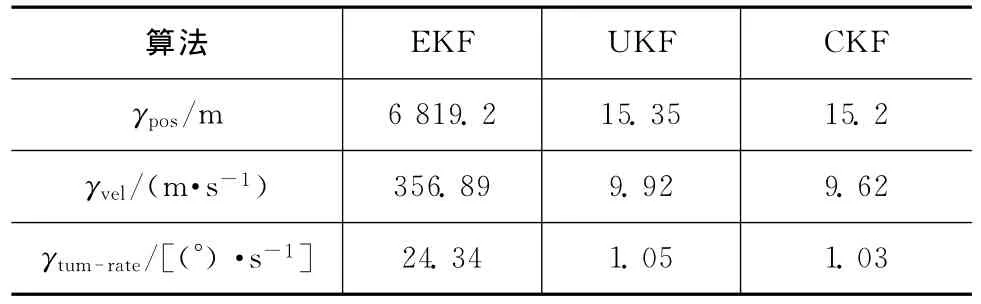
表1 RTAMSE表Tab.1 RTAMSE table

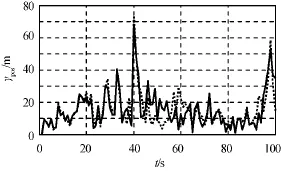
图2 位置均方根误差Fig.2 RMSE in position

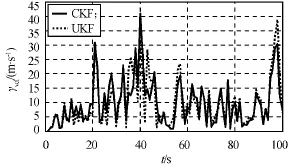
图3 速度均方根误差Fig.3 RMSE in velocity

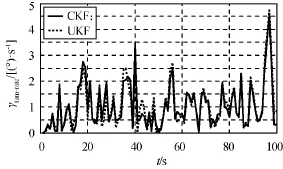
图4 角速度均方根误差Fig.4 RMSE in turn rate

5 结束语

本文对仅有角度和距离测量条件下的一种无源目标跟踪算法进行了研究。采用容积滤波作为跟踪算法，提出基于龙贝格－马尔塔（LM）算法改进的迭代容积无源跟踪算法以提高跟踪精度。仿真结果验证了迭代容积滤波算法有良好的跟踪精度。

［1］ BALAKRISHNAN S N.Extention to modified polar coordinates and application with passive measurements［J］.Journal of Guidance，Control，and Dynamics，1989，12（6）：906－912.

［2］ SONG，T L SPEYER J.A stochastic analysis of a modified gain extended Kalman filter with applications to estimation with bearings only measurements［J］.IEEE Transactions on Automatic Control，1985，30（10）：940－949.

［3］ SONG T L.Observability of target tracking with bearing－only measurements［J］.IEEE Trans on Aerosp Electron Syst，1996，32（4）：1468－1471.

［4］ CADRE J P，JAUFFRET C.Discrete－time observability and estimability analysis for bearings－only target motion analysis［J］.IEEE Trans on Aerosp Elec－tron Syst，1997，33（1）：178－201.

［5］ 孙仲康，郭福成，冯道旺，等.单站无源定位跟踪技术［M］.北京：国防工业出版社，2008：186－199.

［6］ CRASSIDIS J，JUNKINS J.Optimal estimation of dynamic systems［M］.Boca Raton：Chapman ＆Hall，2004：419－433.

［7］ ARASARATNAM I，HAYKIN S.Cubature kalman filters［J］.IEEE Transactions on Automatic Control，2009，54（6）：1254－1269.

［8］ 周 荻，胡振坤，胡恒章.自适应推广Kalman滤波应用于导弹的被动制导问题［J］.宇航学报，1997，18（4）：31－36.