转台高精度模拟卫星三轴角速度解耦算法研究
2014-12-31叶立军王静吉朱文山
叶立军,王静吉,朱文山
(上海航天控制技术研究所,上海 200233)
0 引言
卫星发射前须做大量半物理仿真试验,需要地面设备给出尽可能真实的卫星运动状态。陀螺几乎用于各种姿态基准,当卫星姿态超差,卫星姿态角速度过大时,仅陀螺可作为姿态测量基准;对处于稳态的高精度三轴稳定卫星,姿态基准为星敏+陀螺+Kalman滤波;星敏不可用时,选用精度较低的轨道罗盘时也须应用陀螺。陀螺的测量噪声直接影响姿态精度。在轨道罗盘姿态确定算法中,陀螺的常值漂移误差直接决定偏航姿态角的确定精度,如能在地面测得准确的陀螺常值漂移,并用此常值漂移对陀螺测量角速度进行补偿,便能提高轨道罗盘的姿态确定精度。
陀螺测试转台主要由高精度转台及其控制系统组成。三轴转台由ψ轴转台、θ轴转台、φ轴转台3个子系统组成,分别实现3轴转动。各子系统由台体、驱动系统、转动系统及执行机构组成。选用步进电机作为各子系统驱动装置,经蜗轮蜗杆及齿轮减速后输出旋转运动。转台的3个子系统中,θ轴转台固定在ψ轴转台的转盘上,φ轴转台固定在θ轴转台的转盘上。将被测试陀螺固定于φ轴转台的转盘上,动力学控制转台各轴进行旋转,模拟卫星运行中的角速度,陀螺输出相应的角速度信息,比较动力学姿态与陀螺积分值,即可算出陀螺的常值漂移。
转台解耦控制的研究现已成熟[1-4]。但基于用户角度,用转台模拟卫星姿态角速度,各轴框架不正交可导致耦合,框架偏离角越大,耦合现象越严重。若中框转至与外框重合,则转台控制会出现奇异。针对目前传统处理法存在的缺陷,本文对一种新型转台解耦算法进行了研究。
1 传统处理法及其缺陷
由于陀螺的外框转角对中框和内框无耦合效应,故用转台外框模拟卫星在惯性空间中(卫星的俯仰角速度)角速度的快变量,卫星的滚动和偏航角速度相对为慢变量,在转台上不会导致转台的快速变化,也不会因转台转角过大而产生耦合。以此用三轴稳定卫星角速度特性实现转台的解耦。
传统处理法避免了转台转角过大使转台产生耦合,但存在如下缺陷:
a)直接用动力学欧拉角速率模拟卫星本体的角速度,不考虑欧拉角转序与卫星绕其本体轴旋转角速度的关系;
b)转台三轴运动会出现三轴不正交而产生耦合,耦合随转角变大而加重,会导致陀螺失真;
c)卫星在大气层外运动,不受地球自转影响,而转台固连于地球,地球自转会对转台产生激励,陀螺的测量值也不可避免地渗入了地球自转角速度,影响转台模拟卫星真实转动角速度的精度。
2 转台解耦算法
2.1 欧拉角速率转换为陀螺角速率
地面半物理试验时,由动力学将算得的欧拉姿态角速率送出,地面转台模拟卫星,使陀螺获得相应的卫星本体角速度,欧拉角速率与陀螺测量的本体角速度的关系如下。
令φ,θ,ψ分别为卫星x、y、z轴欧拉姿态角,星体绕其主惯量轴的转动角速度ω在星体坐标中可表示为

式中:xb,yb,zb分别为卫星本体x、y、z轴单位矢量。
此转速可视为3次欧拉转动的合成,卫星欧拉角转序一般定义为3-1-2,即
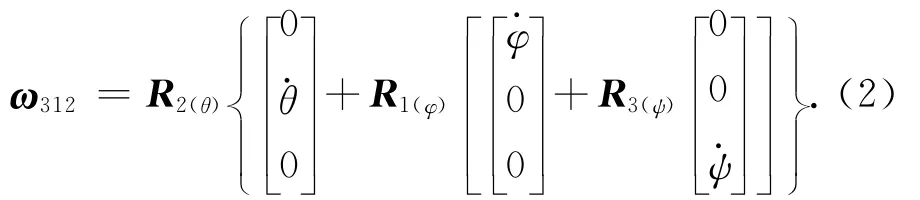

将R1(φ),R2(θ),R3(ψ)代入式(2),可得
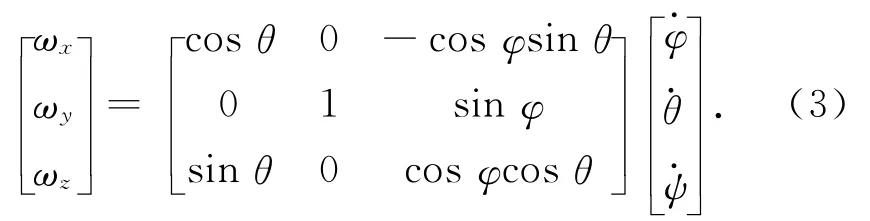
陀螺安装于星体主惯量轴上,其测量所得为卫星本体相对惯性空间的角速度ωi,故需将ω投影至惯性系中。
在轨道坐标系上有-ω0的分量,ω0为卫星的轨道角速度,对任意姿态角φ,θ,ψ,用欧拉角3-1-2转序,得出轨道角速度ω0投影至卫星本体轴上的系数矩阵

将R1(φ),R2(θ),R3(ψ)代入式(4)可得

式中:a11=cosθcosψ-sinφsinθsinψ;a12=cosθ×sinψ+sinφsinθcosψ;a13= -cosφsinθ;a21=-cosφsinψ;a22=cosφcosψ;a23=sinφ;a31=sinφsinθcosψ+cosθsinψ;a32=sinθsinψsinφcosθcosψ;a33=cosφcosθ。
故陀螺测量角速度ωi可表示为

将式(3)、(5)代入式(6),化简得

2.2 框架角解耦算法
转台框架与陀螺安装如图1所示。图中:圆柱体为陀螺,其坐标系为O-x1y1z1;陀螺外围的方框为转台三自由度转动平台,其坐标系为O-XYZ。其中最大方框为转台外框,中间与之相连的较小方框为转台中框,转台内框又与转台中框相连,外框转动作用于中框,中框的转动又作用于内框,内框一维自转,即可模拟卫星三轴角运动。陀螺固连于转台内框,故陀转台内框所处平面代表陀螺平面,在地面进行半物理仿真时,转台模拟卫星,并给陀螺提供三轴角速度信息。

图1 转台和陀螺坐标系Fig.1 Coordinate system of turntable and gyro
当转台三轴处于正交状态时,能精确模拟卫星三轴角运动,可随外界输入条件的变化,转台内中外3个框架不再正交,使陀螺所测角速度与动力学传给转台的角速度存在误差,故需设计一种算法,使陀螺能正确敏感动力学角速度。
陀螺安装于转台的内框,当陀螺测量坐标系与转台一致时,陀螺Z轴总与内框转轴重合,故陀螺可感应到内框转动角速度。由于转台内框安装在中框上,中框的转动角速度的一部分也会投影至内框;同理,中框安装在外框上,外框的转动角速度的一部分也会投影至中框,进而投影至内框。
设某时刻外框(y轴),中框(x轴),内框(z轴)3个框架的转角为B,A,C,其中B为外框相对当地地平面的夹角,A为中框相对外框的夹角,C为内框相对中框的夹角。与此相对应的转台3个框架的角速度为b,a,c,陀螺输出的角速度为ωiy,ωix,ωiz,此时安装在内框的陀螺所测角速度
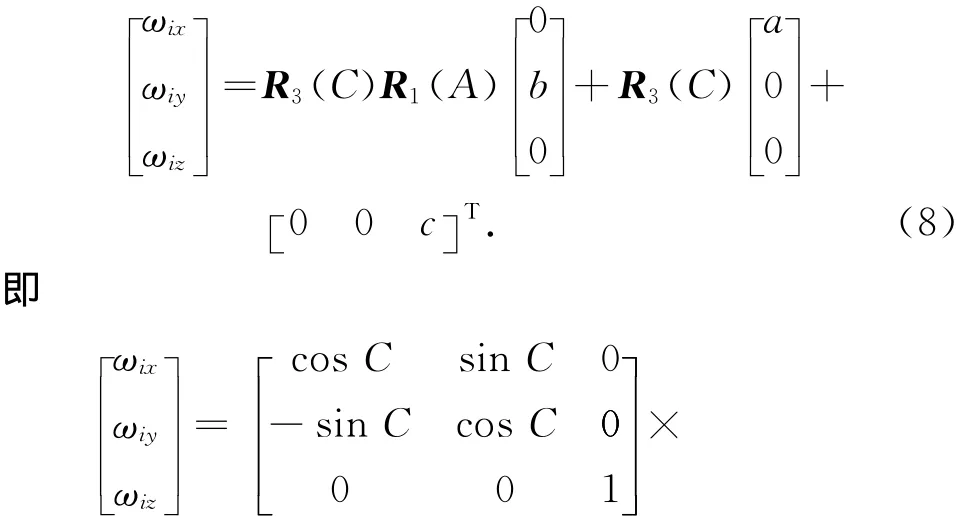

展开得

解得转台输出角速度为
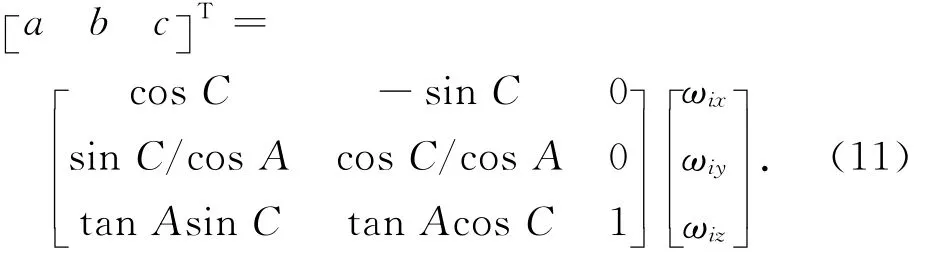
2.3 消除地速影响的转台解耦算法
真实情况下,转台固连于地球,随同地球旋转,为“南东天”坐标系,即(y轴)外框指向东,(x轴)中框指向地球南极,(z轴)内框指向天。设转台置于地球纬度为L的某处,地球在转台+Z向有一个固定的输入Ω0,故此时安装在内框的陀螺所测角速度

算得转台输出的角速度
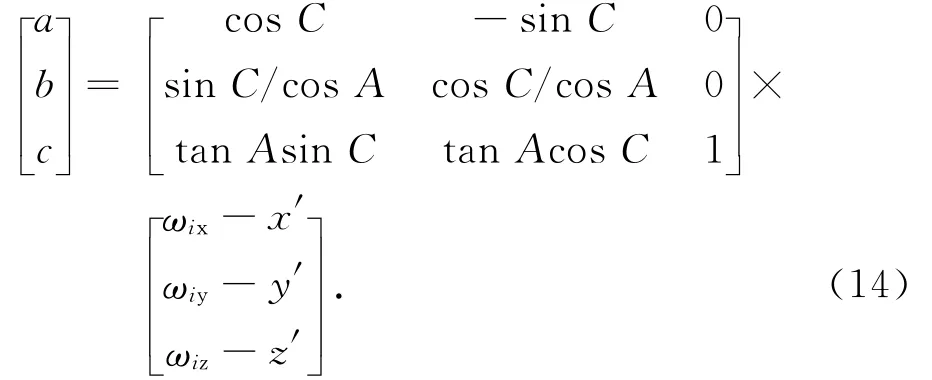
式中:u1=-Ω0cosCcos(L-B)+Ω0sinAsin(LB)sinC;u2=Ω0sinCcos(L-B)+Ω0cosC×sinAsin(L-B);u3=Ω0cosAsin(L-B)。
3 框架角解耦算法仿真与分析
由式(12)可知,转台角速度输出与转台外框角度无关。令陀螺响应转台ωix=ωiy=ωiz=1,以中框和内框角度为自变量,分别以外框三轴输出角速度为变量,可获得三轴转台框架角不同初始角的陀螺感应角速度如图2~4所示。当中框与外框重合即A=90°时,外框的转速会出现奇异。因为当中框与外框重合并均处于地平面时,无论转台如何转动,均不能使陀螺敏感出Z轴方向的角速度。为不使转台计算时产生奇异,应避免中框与外框重合,即A≠90°。故取转台中框转角范围A∈[-80°,80°],取转台内框转角范围C∈[-180°,180°],所得结果如图2所示。

图2 不同初始角的转台X轴角速度Fig.2 X-axis angle velocity with various initial angle
由图2可知:中框角A对(X轴)转台中框角速度无影响,不同的内框转角对应不同的中框角速度,且中框转动角速度不会出现奇异。

图3 不同初始角的转台Y轴角速度Fig.3 Y-axis angle velocity with various initial angle
由图3可知:中框角A和内框角C对于(Y轴)转台外框的角速度均有影响,当中框角度A越接近±90°,外框角速度越大,越易产生奇异。
由图4可知:中框角A和内框角C对转台内框的角速度均有影响,且当中框角度A越接近±90°,内框角速度越大,越易产生奇异。当内框与中框的框架角均为0°时,转台3个框架角的角速度刚好等于陀螺感应的3个角速度。这表明3个框架角正交性越好,转台的解耦性越好。由以上分析可知:当用转台模拟卫星欧拉姿态角时,应尽量避免中框与内框夹角过小。

图4 不同初始角的转台Z轴角速度Fig.4 Z-axis angle velocity with various initial angle
4 转台改进算法仿真与分析
为模拟卫星真实的角速度信息,卫星与转台三轴对应关系可变。卫星稳态运行时,卫星滚动、俯仰、偏航轴的平均角速度分别为0,0.062 0,0(°)/s,角速度方差3σ=0.005(°)/s,仿真时间10h。
4.1 卫星三轴与转台三轴一致
令卫星本体坐标系与转台坐标系的X、Y、Z轴重合,直接将动力学输出的卫星欧拉角速度作为转台的输入激励,驱动转台转动,此时安装在转台上的陀螺敏感到角速度,并将此角速度值输入星载计算机所得转台的转角和转动角速度输出分别如图5、6所示。

图5 转台框架角Fig.5 Turntable angle
由图5、6可知:当卫星稳态运行,转台坐标系与卫星本体坐标系一致时,转台中框角度随仿真时间增加而接近90°,进而导致外框和内框产生奇异,其角速度也会随之迅速变大,陀螺测量值较易失真,不利于转台模拟卫星姿态的变化。

图6 转台框架角速度Fig.6 Turntable angle velocity
4.2 改进陀螺与转台轴的对应关系
由于转台中框过90°时会产生奇异,为使转台长期模拟卫星运动,(卫星欧拉角速度的快变量)卫星俯仰轴的角速度不能放置在转台中框X轴,而应放在转台内框Z轴。令卫星滚动轴与转台X轴对应,卫星俯仰轴与转台内框Z轴对应,卫星偏航轴与转台Y轴对应。仿真结果如图7~9所示。

图7 改进后转台框架角Fig.7 Improved middle turntable angle
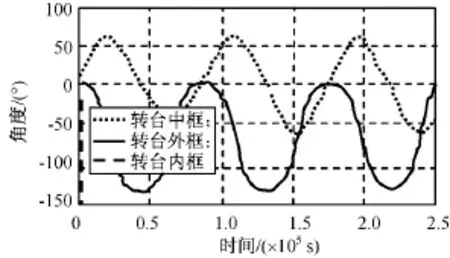
图8 改进后转台框架角Fig.8 Improving turntable angle
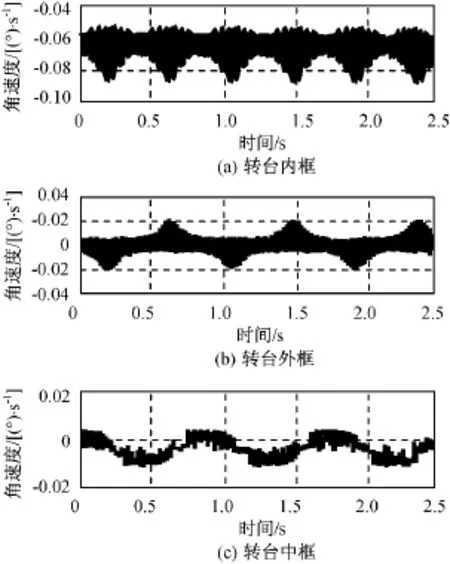
图9 改进后转台框架角速度Fig.9 Improving turntable angle velocitiy
由图7~9可知:当卫星稳态运行,转台的内框模拟卫星俯仰轴,外框模拟卫星偏航轴时,内框转速为快变量,中框和外框转速为慢变量。由于中框最大转角(<60°)较小,故转台不会产生接近奇异的现象,仿真时间为80h时,转台框架角速度变化也较小,且不会发散。
5 结束语
本文通过对传统转台模拟卫星角运动进行仿真,验证并分析了传统算法的不足。设计一种转台解耦算法,理论推导了欧拉角速度到陀螺角速度的转换,框架解耦和消除地速影响的算法。仿真结果表明:卫星初态和稳态运行时,为避免转台接近奇异,应调整卫星坐标系与转台坐标系的关系。
[1] 张锦江,冯汝鹏,陈兴林,等.仿真转台解耦的鲁棒自适应模糊化设计[J].系统仿真学报,2000,12(2):155-158.
[2] 陶渝辉.捷联导引头半实物仿真误差分析[J].现代防御技术,2007,35(3):114-116.
[3] 黄卫全,刘文佳.三轴仿真转台解耦问题的研究[J].弹箭与制导学报,2009,29(1):99-103.
[4] 刘延斌,金 光,何惠阳.三轴仿真转台系统模型建立及解耦控制研究[J].哈尔滨工业大学学报,2003,35(3):323-328.
