摄动条件下椭圆轨道卫星相对运动研究

饶殷睿，殷建丰，韩 潮

（北京航空航天大学 宇航学院，北京 100191）

0 引言

随着航天技术的不断发展，卫星编队飞行因其诱人的应用前景，逐渐成为航天领域的研究热点。编队飞行卫星具高可靠性和编队可重构的优势，主要用于对地观测、精确定位、天文观测以及电子侦察等领域。这些应用对精度的要求很高，因此研究高精度的编队飞行卫星系统相对运动模型意义重要。文献［1］建立了一种系统、准确、稳定、可控，可通过相对测量信息高精度地自主确定的相对运动模型，采用球面几何方法，严格定义了相对轨道要素，推导了开普勒轨道条件下高精度椭圆轨道近距离相对运动方程［2］。本文称其为经典相对轨道要素描述的相对运动模型。但卫星在实际运行中会受到地球非球形引力、第三体引力、太阳光压、大气阻力等多种摄动力的作用［3］。在摄动力的影响下，编队飞行卫星的轨道根数及相对轨道会发生变化，虽然这些摄动力与地球中心引力相比非常小，但长期作用仍可使卫星轨道偏离卫星应用任务的要求［4］。因此，在需要高精度轨道预报的卫星编队飞行研究中，这些摄动力不能被忽略。编队飞行卫星的摄动分析方法主要有动力学方法和运动学方法两种。动力学方法主要是求解Hill方程，即将摄动的影响作为力函数添加到Hill方程右端，使其适于摄动条件下卫星相对运动的研究［5］。但这需求解非线性微分方程，难度较大，且仅在某些特殊情况下才能获得解析解［6］。运动学方法是基于运动学模型的摄动分析方法，通过研究轨道根数在各种摄动力影响下的变化分析编队飞行卫星的摄动问题［7］。对此，国内外已有相关研究［8－9］。本文在经典相对轨道要素法的基础上，考虑地球非球形引力、大气阻力及三体引力等摄动力的影响，为相对轨道要素添加相应的摄动项，以推导适于椭圆和近圆摄动轨道的预报算法，拓展相对轨道要素基本理论，对摄动条件下的卫星高精度近距离相对运动模型建立进行了研究，并讨论了该模型的有效性和精度。

1 相对轨道要素定义

文献［1］推导了开普勒轨道条件下相对轨道要素的相关公式，其定义为

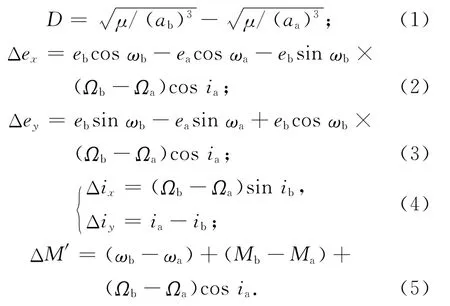
式中：μ为地心引力常数；a为半长轴；i为轨道倾角；e为偏心率；ω为近地点幅角；Ω为升交点赤经；M为平近点角；下标a，b分别表示参考星和伴随星。

对卫星近距离相对运动，在小角度相对运动假设条件下，由一阶线性展开可导出从绝对轨道要素｛a，e，Ω，i，ω，M｝与 相 对 轨 道 要 素 ｛D，Δex，Δey，Δix，Δiy，ΔM′｝间相互转换的直接表达式为

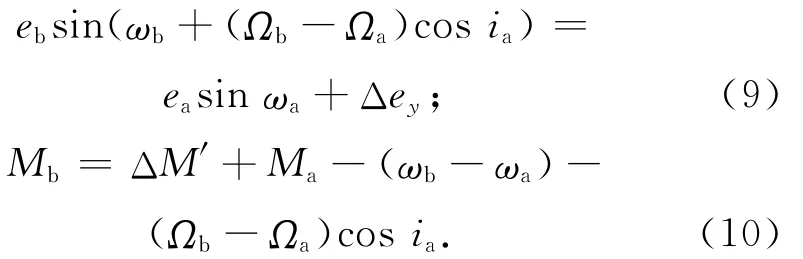
式中：为平均角速度，且

2 摄动力模型

根据文献［10］的摄动力模型，引入拟平均根数定义，令ξ＝ecosω，η＝－esinω，λ＝ω＋M，以a，i，Ω，ξ，η，λ作为新的绝对轨道六要素，以消除e＝0和通约奇点。此处所有参数采用的单位制均为标准单位制，即长度和质量单位各为参考椭球体赤道半径ae和地球质量M，且使引力常数G＝1，相应的时间单位T＝ （（ae）3／（GM））1／2＝806.811 6341s。此处：GM＝3.986 005×1014m3／s2。

2.1 非球形引力摄动

因地球的密度分布并不均匀，其形状亦不是球形，且相当不规则。对人造地球卫星的运动来说，此形状和密度分布的非球形部分是不可忽视的一种摄动源（地球非球形引力摄动）。对近地轨道卫星，主要带谐项J2项摄动是影响其运行轨道的最主要摄动源。卫星在中心引力场和J2项摄动作用下，以σ0表示初始时刻卫星密切轨道根数，其瞬时轨道根数的变化为

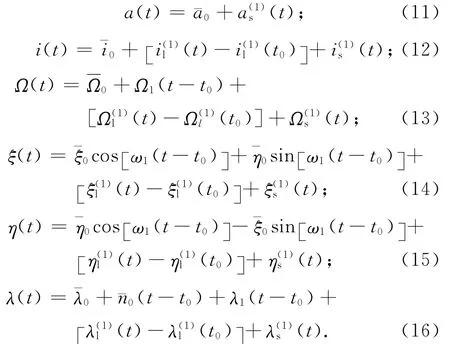
在以上三种摄动项中，对近地卫星轨道影响最大的为一阶长期项，与其相比，短周期项和一阶长周期项的影响可忽略。一阶长期项可表示为

2.2 大气阻力摄动

由于人造地球卫星是在近地空间飞行，特别是低轨道卫星高度仅数百公里，甚至低于200km，大气的阻尼影响较显著，使卫星椭圆轨道不断变小变圆，因此大气也是影响卫星运动的一种主要摄动因素，特别是对那些面质比较大的低轨卫星［11］。为便于研究，作如下假设：大气层受地球扁率的影响，即考虑扁球大气，但不考虑日下点大气密度的突变；大气层旋转角速度与地球自转角速度相同；卫星横截面积S不变［12－13］。则大气阻力摄动的长期摄动项系数可表示为

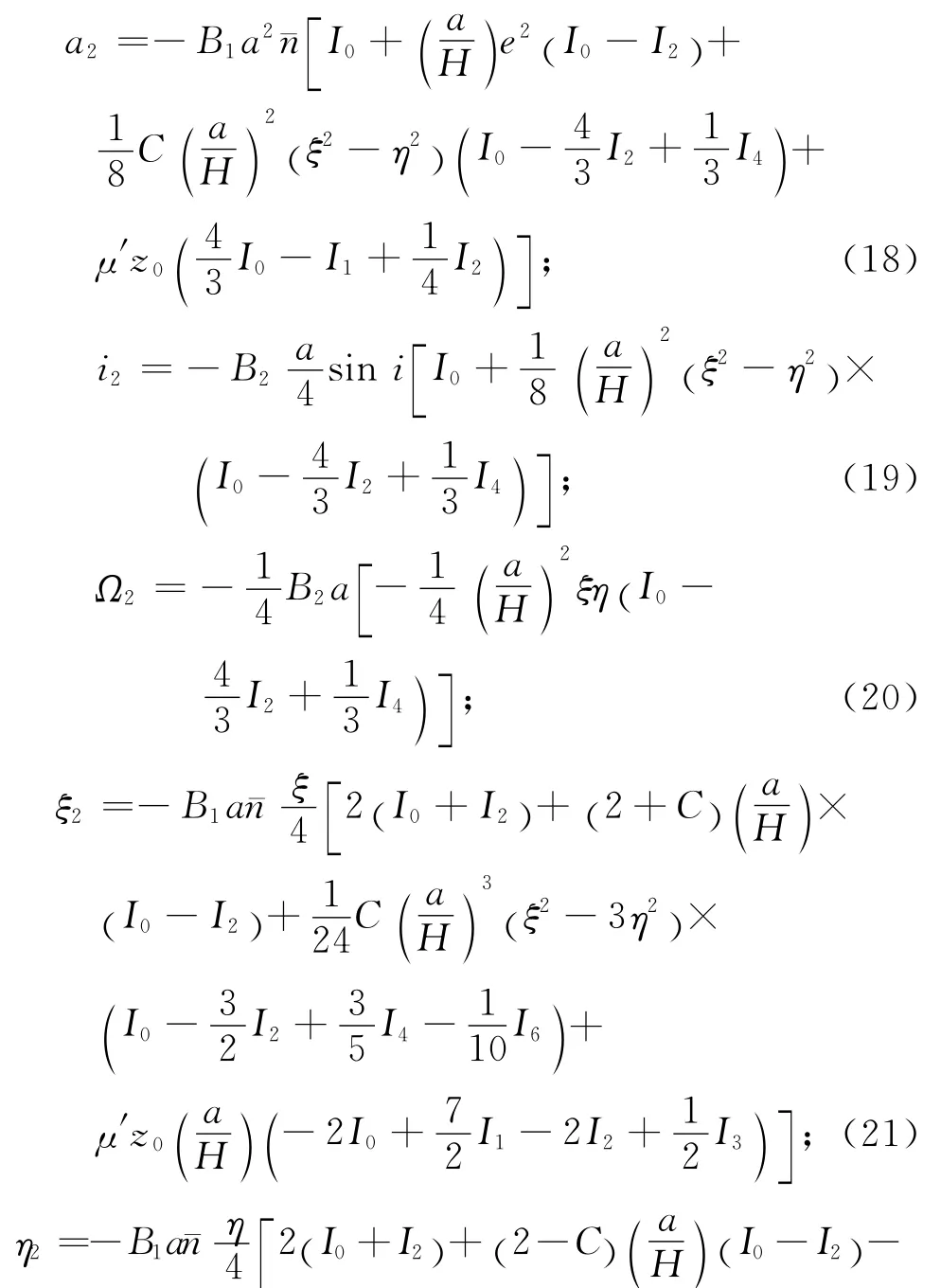
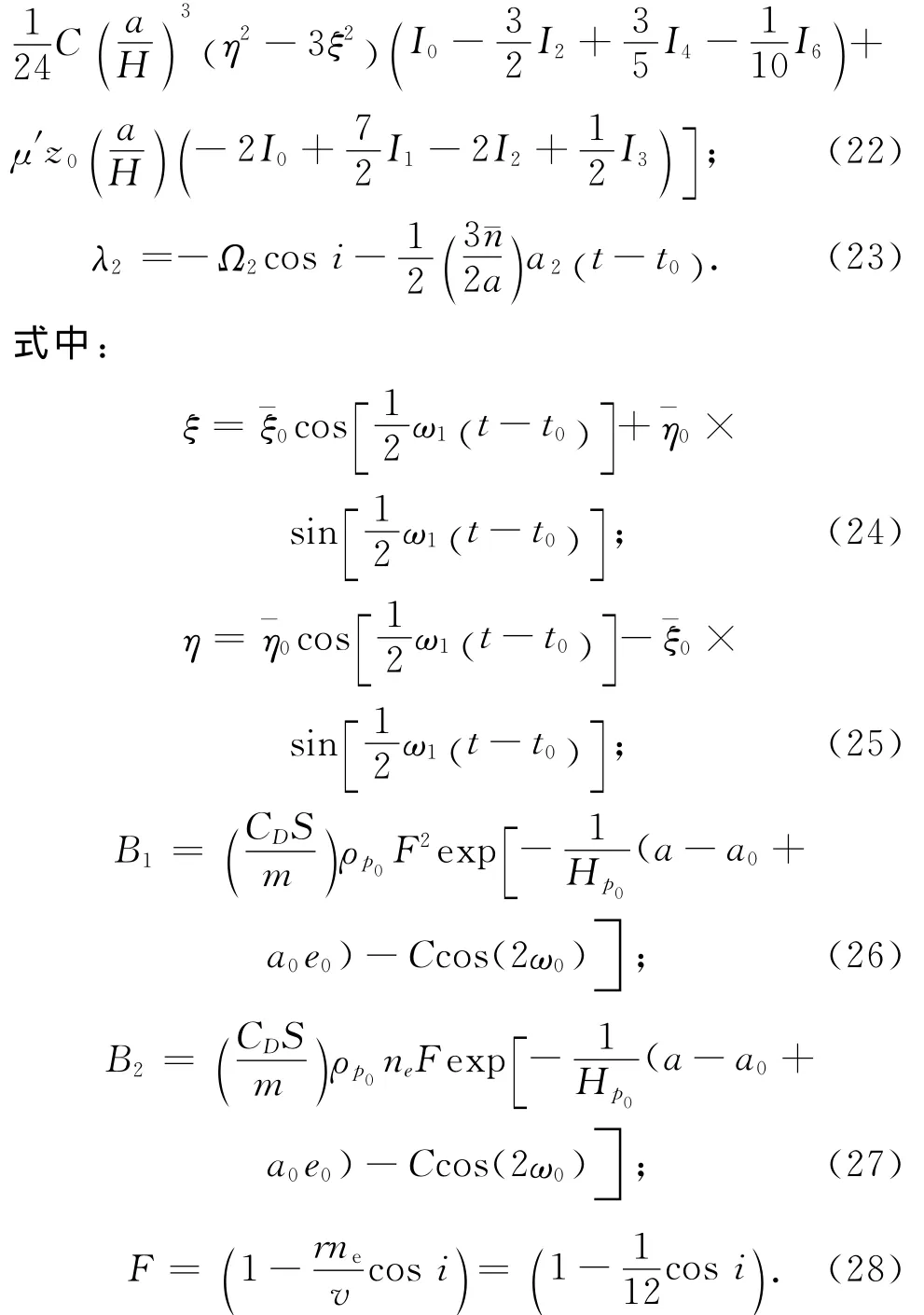
此处：CD＝2.2；C≈0.1；S／m≈109；ne为地球自转角速度；μ′≈0.1；z0＝a0e0／Hp0；ρp0，Hp0分别为卫星轨道初始近地点处的密度和标高；σ0为初始近地点处的轨道根数；In（z）（n＝1，…，6）为第一类虚变量的贝塞尔函数［14－15］。为表达简洁，式（21）～（25）中In（z）均简写为In。

2.3 三体引力摄动

日、月和大行星的引力作用对人造地球卫星尤其是远地卫星运动的影响，是天体力学中的一种典型的第三体摄动问题。虽然这类摄动力也是一种保守力，但由于日、月和地球、卫星相距都不太远，问题显得较复杂。对高精度要求，日、月和地球不能简单视作质点，而应精确计算日、月的位置。本文主要考虑日月摄动引起的卫星轨道变化的三个摄动项中的二阶长期项σc（t－t0），有

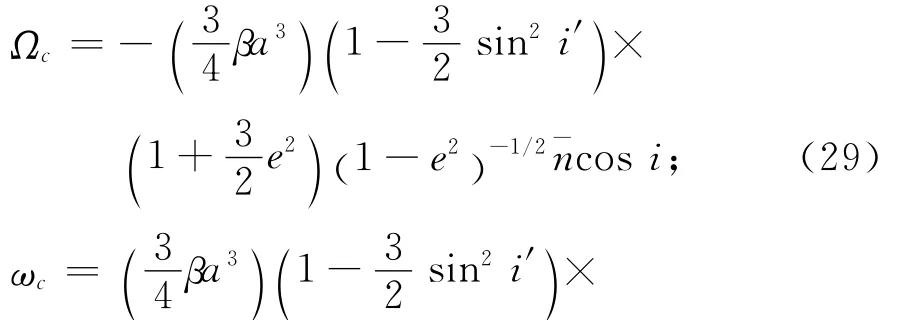
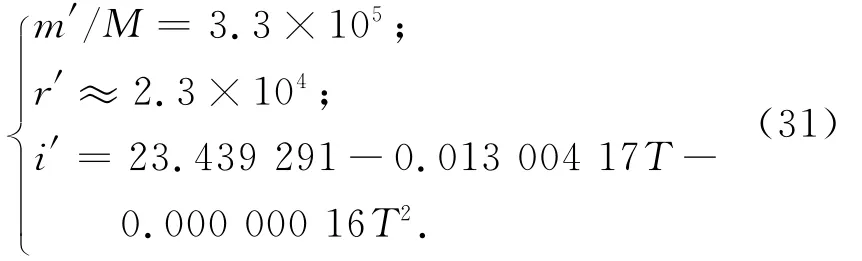
对月球，有

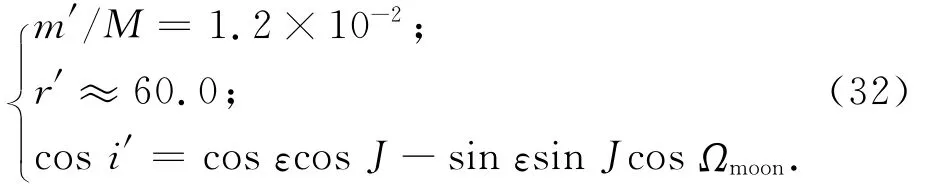
式中：

3 摄动条件下基于相对轨道要素的椭圆基准轨道的相对运动描述

3.1 相对轨道要素变换

根据前文提到的拟平均根数法，令ξi＝eicosωi，ηi＝－eisinωi，λi＝ωi＋Mi（i＝a，b），并以a，i，Ω，ξ，η，λ作为新的绝对轨道六要素，则相对轨道要素可表示为

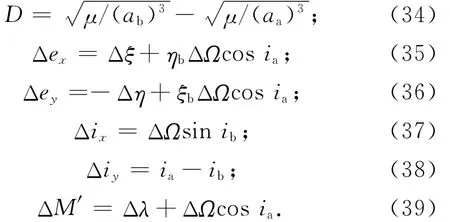
3.2 考虑摄动影响的相对轨道要素计算

将上述各摄动力对卫星轨道根数的影响表达式代入相对轨道要素的定义式中，并将其化为标准单位，可得

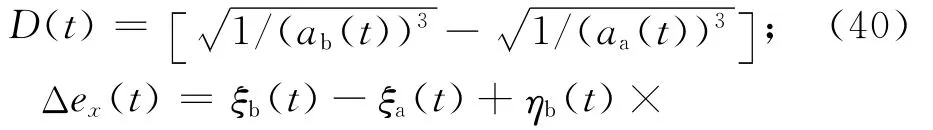
式中：

3.3 椭圆基准轨道相对运动描述

以上述摄动条件下的相对轨道要素为基本参数，建立卫星近距离且考虑摄动力作用时相对距离和相对速度的代数关系，结果适用于摄动条件下的椭圆基准轨道和近圆基准轨道。

根据文献［1］中的结论，可得伴随卫星在基准星质心轨道坐标系中的近距离相对运动方程和速度方程为

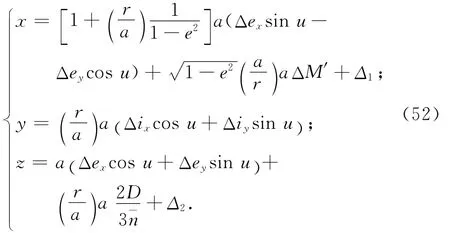
式中：

此处：θ为真近点角；u为纬度幅角；r为轨道矢径的模长；

注：上述各式中参数，a，e，ω均为参考星的瞬时绝对轨道要素；D，Δex，Δey，Δix，Δiy，ΔM′均为瞬时相对轨道要素；r，u均为与时间相关的变量。

将摄动模型中各摄动力影响下的绝对轨道要素（式（17）～（23）、（29）、（30））及相对轨道要素变换中给出的带摄动项的相对轨道要素（式（40）～（45））的表达式代入式（52）～（58），可得摄动条件下伴随星相对参考星的位置速度方程。

对速度方程，需说明的是由于带摄动项的相对轨道要素为时变的，在对位置方程进行求导时也应对其进行求导。但考虑相对轨道要素对时间的导数项对速度的影响较小，且为使模型尽可能简单，故将其略去。

带摄动项的相对轨道要素的椭圆基准轨道相对运动方程的形式与经典相对轨道要素并未复杂太多，但适用范围却有很大拓展。本文给出的带摄动项的相对运动模型，可用于非球形引力、大气阻力、三体引力等摄动力影响下椭圆轨道卫星的相对轨道预报。

4 数值算例

本章算例中的精确解通过高精度轨道预报器精确计算出两颗卫星在地心赤道坐标系中的位置和速度，进而计算两星的相对位置和相对速度，最后投影到轨道坐标系得到［16］。

算例1：非球形引力摄动在近地椭圆基准轨道卫星相对运动中的影响分析

选择高精度轨道预报器的摄动类型为非球形引力摄动，编队飞行特征尺度1km，基准轨道偏心率0.01，典型的初始轨道参数见表1。

考虑与不考虑非球形引力摄动相对运动分析结果如图1所示。卫星运行10圈的误差值统计结果见表2。

由图1、表2可知：在考虑非球形引力摄动影响时，对近地椭圆基准轨道而言，无摄动项的椭圆相对运动模型误差非常大，本文给出的带非球形引力一阶长期摄动项的椭圆相对运动模型较好地适应了非球形引力摄动对椭圆基准轨道的影响，相对轨道预报精度误差保持在十米级的标准，相对误差具有百分之几的量级精度。

说明：在考虑非球形引力摄动的影响时，在相对轨道要素中并未加入短周期项，主要是因为短周期项对卫星相对轨道的影响量级仅约1%，故可忽略。短周期项影响下卫星相对位置和相对速度误差如图2所示。由图可知：与一阶长期项相比，短周期项的影响很小，故在为经典相对轨道要素添加非球形引力摄动项时，只添加一阶长期项部分既可简化瞬时相对轨道要素计算的复杂性，又不降低太多精度，是合理的。

表1 算例1中卫星A、B的初始轨道参数Tab.1 Orbit parameters of satellite A and B in case 1

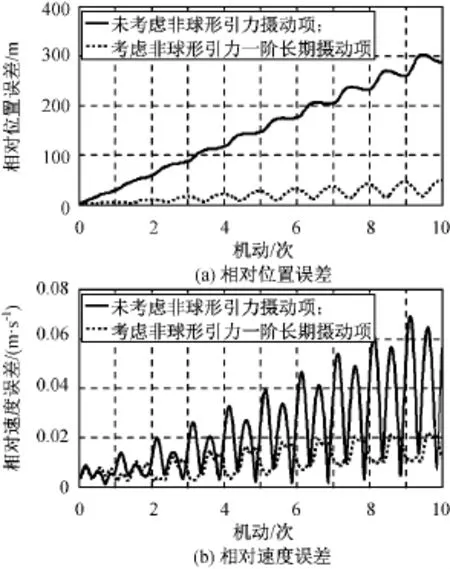
图1 非球形引力影响下卫星相对位置和相对速度误差Fig.1 Errors of relative position and relative velocity under effect of nonspherical gravitational perturbation

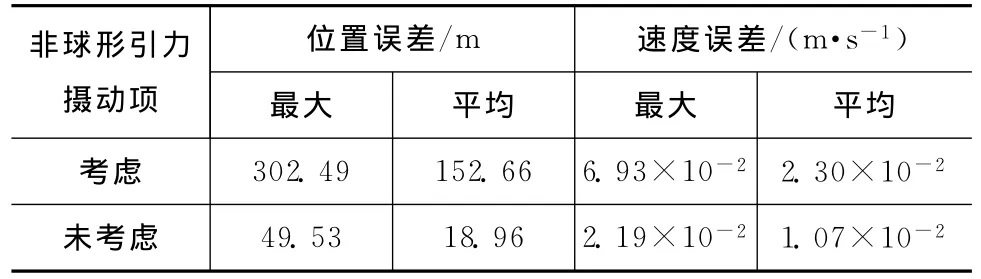
表2 算例1中卫星运行10圈后相对位置和相对速度误差Tab.2 Errors of relative position and relative velocity after 10periods in case 1

算例2：大气阻力摄动在近地轨道卫星相对运动中的影响分析

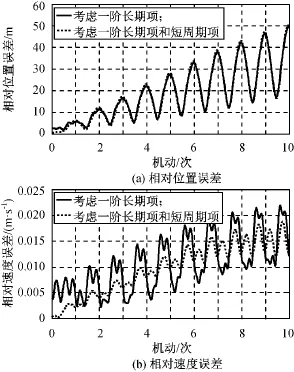
图2 短周期项影响下卫星相对位置和相对速度误差Fig.2 Errors of relative position and relative velocity under effect of short periodic term

选择高精度轨道预报器的摄动类型为非球形引力摄动＋大气阻力摄动，编队飞行特征尺度为1km，基准轨道偏心率为0.001，典型的初始轨道参数见表3。说明：由于大气阻力对近地轨道卫星影响较大，且在圆轨道的情况下会更明显，故算例中的基准轨道取为近圆轨道。

考虑和未考虑大气阻力摄动时相对运动分析的结果如图3所示。卫星运行10圈的误差统计结果见表4。

由图3和表4可知：考虑大气阻力摄动影响时，对近地轨道来说，无大气阻力摄动项的相对运动模型误差仍很大，本文给出的带大气阻力长期摄动项的相对运动模型可较好地反映大气阻力对近地轨道卫星近距离相对运动的影响，相对轨道预报精度误差保持在1m级的标准，相对误差有百分之几的量级精度。

表3 算例2中A、B卫星的初始轨道参数Tab.3 Orbit parameters of satellite A and B in case 2

图3 大气阻力影响下卫星相对位置和相对速度误差Fig.3 Errors of relative position and relative velocity under effect of atmospheric drag perturbation

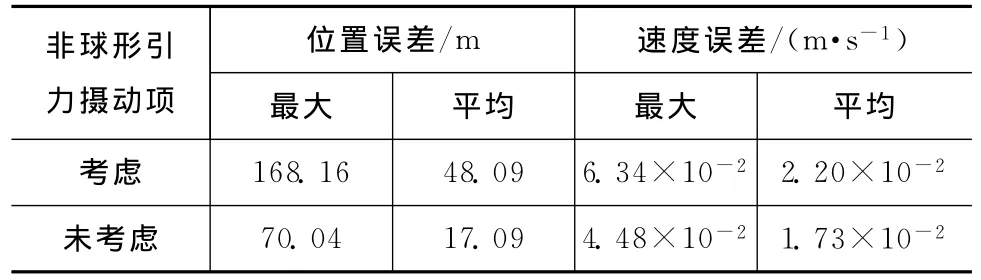
表4 算例2中卫星运行10圈后相对位置和相对速度误差Tab.4 Errors of relative position and relative velocity after 10periods in case 2

算例3：三体引力摄动在远地椭圆基准轨道卫星相对运动中的影响分析

选择高精度轨道预报器的摄动类型为非球形引力摄动＋日月引力摄动，编队飞行特征尺度为1km，基准轨道偏心率为0.01，典型的初始轨道参数见表5。

图4 三体引力影响下卫星相对位置和相对速度误差Fig.4 Errors of relative position and relative velocity under effect of third body gravitational perturbation

考虑和未考虑三体引力摄动时相对运动分析结果如图4所示。卫星运行10圈的误差统计结果见表6。由图4和表6可知：考虑三体引力摄动影响时，对远地椭圆基准轨道来说，无三体引力摄动项的椭圆相对运动模型误差较大，本文给出的带三体引力长期摄动项的椭圆相对运动模型在一定程度上减小了因日月引力摄动造成的轨道预报误差，相对轨道预报精度误差保持在米级的标准，相对误差具有千分之几的量级精度。

算例4：相对轨道要素在摄动条件下的特性分析

由前三个算例已发现，非球形引力摄动、大气阻力摄动以及三体引力摄动对卫星近距离相对运动轨道的影响很大，不可忽略。经典相对轨道要素与带摄动项的相对轨道要素分别描述的相对运动模型的误差较大的原因是：在摄动条件下，相对轨道要素随时间不断变化，而经典相对轨道要素是常量，其预报的相对运动轨道与精确解间的误差较大。取与算例1相同的基准轨道参数，考虑非球形引力、大气阻力、三体引力等三种摄动力的影响，计算各时刻相对轨道要素的值，并求得其与高精度轨道预报器计算得到的瞬时相对轨道要素的精确值的相对误差，再同经典相对轨道要素与精确值的相对误差进行对比，结果如图5所示。

表5 算例3中卫星A、B的初始轨道参数Tabl.5 Orbit parameters of satellite A and B in case 3

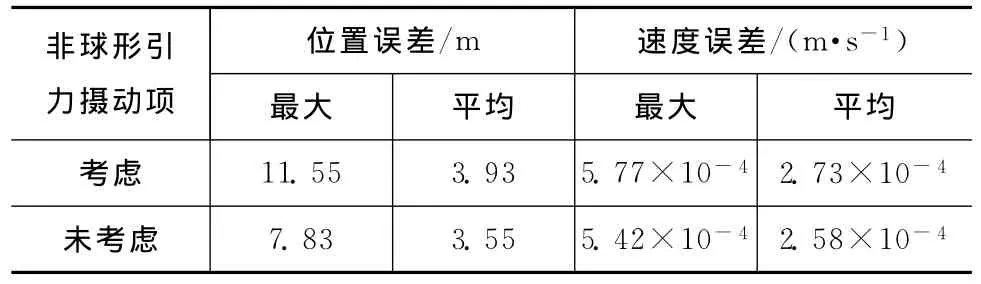
表6 算例3中卫星运行10圈后相对位置和相对速度误差Tab.6 Errors of relative position and relative velocity after 10periods in case 3

由图5可知：加入摄动项后，瞬时相对轨道要素与精确值的相对误差明显减小至约0.5%，而相对轨道要素的值的精度直接关系最后求得的卫星相对运动的位置和速度的精度。因此，在摄动条件下，为经典相对轨道要素添加摄动项非常有必要且有效。

说明：由于初始给定的相对轨道要素D，ΔM′均为0，故只计算了Δex，Δey，Δix，Δiy的相对误差。由式（40）～（51）可知，摄动项中只有大气阻力的长期摄动项对Δiy（t）有影响，故与其他几项相对轨道要素摄动项相比，添加与否的影响较小，图5中经典相对轨道要素中Δiy（t）与精确值的相对误差和带摄动项的相对轨道要素中Δiy（t）与精确值的相对误差接近（相对误差曲线基本重合）。

算例5：相对运动模型精度分析

设典型初始轨道参数见表7，初始相对轨道要素按比例增加，并且卫星运行的圈数从10圈到100圈依次增加。表中：S为相对运动尺度，从1km到10km以1km为步长递增。仿真结果如图6～8所示。

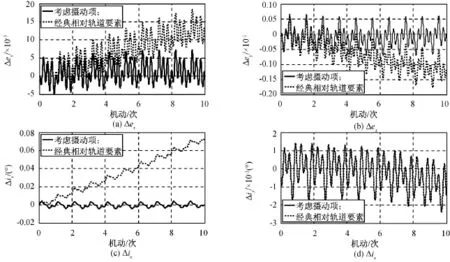
图5 相对轨道要素误差分析Fig.5 Errors of relative orbit elements

表7 算例5中A、B卫星的初始轨道参数Tab.7 Orbit parameters of satellite A and B in case 5

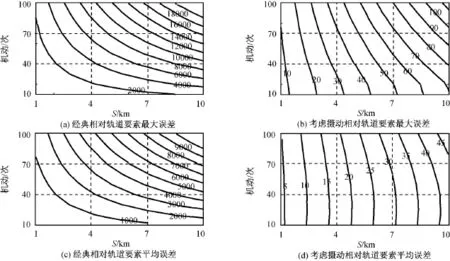
图6 两种相对运动模型的相对轨道要素误差Fig.6 Relative elements errors of two relative models

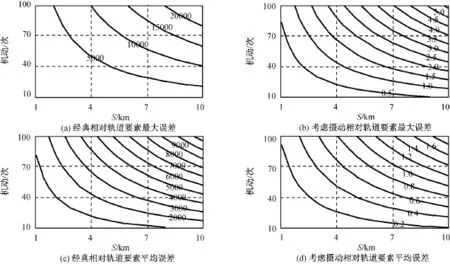
图7 经典相对轨道要素运动模型位置速度误差Fig.7 Relative position and velocity errors of classical relative orbit elements model

比较图6～8可知：典型相对轨道要素描述的卫星近距离相对运动模型的相对轨道要素和相对位置速度的误差，随圈数和相对运动的尺度增加而急剧增大，而带摄动项的相对轨道要素描述的运动模型的误差，随圈数以及相对运动的尺度增加的趋势不明显，出现误差主要是由模型线性化导致。在低轨道上，带摄动项的相对轨道要素运动模型的精度明显高于经典相对轨道要素运动模型。这进一步表明本文给出的带摄动项的相对轨道要素运动模型有更强的轨道类型的适应性和预报精度。

图8 带摄动的相对轨道要素运动模型位置速度误差Fig.8 Relative position and velocity errors of relative orbit elements with perturbation model

5 结束语

本文对摄动条件下椭圆轨道卫星相对运动进行了研究。研究发现：本文基于文献［1］给出的开普勒轨道的相对轨道要素，采用拟平均根数法，消除奇点情况，为其添加非球形引力、大气阻力、三体引力部分摄动项，由此得到带摄动项的相对轨道要素，其形式简单，便于拓展，适用范围广，且易于与精确解进行误差分析。算例表明，其与精确解的相对误差保持在约0.5%，因此是正确而有效的。各种摄动力对卫星相对运动中的相对位置和相对速度均有很大的影响，不能忽略。文中给出的带摄动项的相对轨道要素法提高了预报精度，其预报卫星相对运动轨道的误差较采用经典的相对轨道要素法最多可减少近90%。本文推导的带摄动项相对轨道要素描述的卫星近距离相对运动模型，形式简单，计算速度快，与通过积分方法得到的精确解相比，误差保持在十米量级，提供的模型精确有效，为卫星编队飞行的轨道预报提供了一种新的参考模型。研究结果统一了开普勒轨道和摄动轨道的近圆和椭圆基准轨道卫星相对运动描述形式，这为轨道摄动条件下椭圆轨道卫星编队飞行的研究提供了便利和精度保证。

［1］ 韩 潮，殷建丰.基于相对轨道要素的椭圆轨道卫星相对运动研究［J］.航空学报，2011，32（12）：2244－2258.

［2］ TAFF L G.Computational spherical astronomy［M］.New York：Wiley，1981.

［3］ XU Guo－chang.Orbits［M］.Berlin Heidelberg：Spinger－Verlag，2008.

［4］ 孟 鑫，李俊峰，高云峰.卫星编队飞行中相对轨道的J2摄动分析［J］.力学学报，2006，38（1）：89－96.

［5］ HILL G W.Researches on the lunar theory［J］.A－merican Journal of Mathematics，1978，1（3）：245－260.

［6］ 张玉锟，戴金海.卫星编队飞行的地球扁率摄动分析［J］.宇航学报，2002，23（3）：72－76.

［7］ 张 娟，和兴锁，邓峰岩，等.编队飞行星座的地球扁率摄动和大气阻力摄动分析［J］.应用力学学报，2006，23（3）：496－450.

［8］ 杨 宇，韩 潮.编队飞行卫星群描述及摄动分析［J］.中国空间科学技术，2002，22（2）：15－23.

［9］ ALFRIRND K T，SCHAUB H，GIM D W.Gravitational perturbations nonlinearity and circular orbit assumption effects on formation flying control strategies：Annual AAS Rocky Mountain Guidance and Control Conference［C］.2000.

［10］ 刘 林.航天器轨道理论［M］.北京：国防工业出版社，2000.

［11］ 刘 林.人造地球卫星轨道力学［M］.北京：高等教育出版社，1992.

［12］ KING－HELE D G.Analysis of the orbit of 1970－114Fin its last 20days［J］.Planet，Space Sci，1976，24（1）：1－16.

［13］ KING－HELE D G.Theory of satellite orbits in an atmosphere［M］.London：Butterworths，1964.

［14］ US Government.COESA，US standard atmosphere，1976［M］.Washington DC：US Government Printing Office，1976.

［15］ WATSON G N.Theory of Bessel functions［M］.London and New York：Combridge Univ Press，1994.

［16］ 肖业伦.航天器飞行动力学原理［M］.北京：宇航出版社，1995.