一个扩展的可积Broer－Kaup方程族

于 义

孤立子与可积系统方向是当今非线性科学研究的主流方向，在光纤通讯、浅水波、等离子体、磁流体、超导等科技领域有着重要的应用背景。其研究涉及众多主干数学分支，包括常微分方程、偏微分方程、泛函分析、微分几何、椭圆函数、代数函数、代数曲线、微分拓扑、辛几何、李群与李代数及表示论、无穷维李代数等［1－4］。该研究对许多数学分支及交叉学科的发展都有着重要影响和促进作用。自从反散射方法发现以来，可积系统及孤立子理论不仅在数学、物理、化学、生物通讯领域得到了广泛深入的研究和应用，而且迅速拓展到生物、光学、材料、天体等自然科学的各个领域。作为非线性科学的核心问题，可积孤子方程有几个重大的特征:一是孤立子解，二是Backlund变换，三是无穷多守恒律，四是散射反演法。正是这些特点促使可积系统成为当今世界研究的热点问题之一［5－7］。本文将利用圈－李代数方法构造一个新的可积方程族。

1 矩阵圈代数

它们具有如下的交换子运算

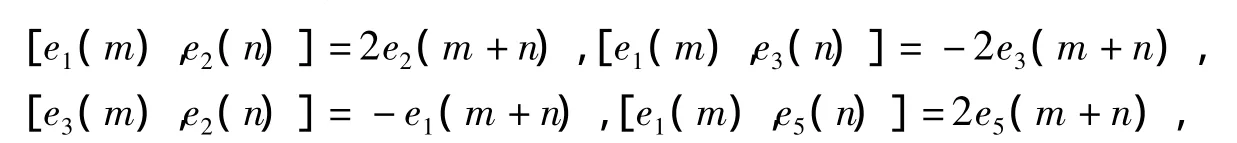
定义阶为

2 扩展的Broer－Kaup方程族

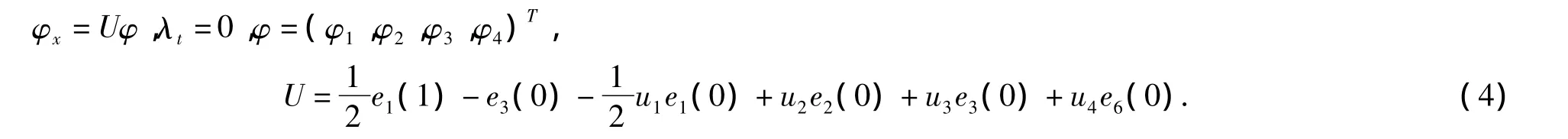
由驻定零曲率方程

得

则方程(5)化为

可知，(7)左面的阶≥0，而右面的阶≤0。因此，(7)的阶为0。由此

取修正项 Vn，即 V(n)=+Vn，Vn=cn+1e1(0).

进而，由零曲率方程

得

其中 J 为 Hamiltonian 算子，M1=－u3－u3+2u2－2u2－1u2，

M2=－－u1－2u2－1+u4+u1u4，M3=－2－1u2－+u1+u4－u1u4.

利用(6)，可以得到递推算子L，

这里 l1=u3+－1u3－2u2－2－1，l2=2u4－1u2+4－1u2，

l3=2－1u2+u1－，l4=+u1+2 u2－1.

因此，系统(9)可以写为

当n=2时，得到下面的非线性演化方程

特别地，在(11)中，取 u1=q，u2=r，u3=u4=0，得

方程(12)恰为著名的Broer－Kaup方程。由此可见方程族(10)为Broer－Kaup方程的扩展可积模型。

［1］谷超豪.孤立子理论与应用［M］.杭州:浙江科技出版社，1990.

［2］谷超豪.孤立子理论中的Darboux变换及其几何应用［M］.上海:上海科技出版社，1999.

［3］李翊神.孤立子与可积系统［M］.上海:上海科技出版社，1999.

［4］曹策问.保谱方程的换位表示［J］.科学通报，1989，34(10):723－725.

［5］马文秀.一个新的Liouville可积的广义Hamilton方程族及其约化［J］.数学年刊，1992(1):115－124.

［6］Zhenya Yan.Two types of hierarchies of evolution equations associated withthe extended Kaup－Newell spectral problem with an arbitrary smooth function［J］.Chaos，Solitons and Fractals，2003，15(4):639－645.

［7］Guizhang Tu.A trace identity and its application to integrable systems of 1+2 dimensions［J］.J.Math.Phys，1991，32(7):1900－1907.