Mathematica在有心力教学中的应用研究

2014-12-28谢文海刘德民

长春师范大学学报 2014年4期

杨硕，谢文海，刘德民

(1.大连大学物理科学与技术学院，辽宁大连116622;2.江南大学物联网工程学院，江苏无锡214122)

如果运动质点受到的力及其作用线总是通过空间中某一固定点，这种力叫做有心力［1］。理论物理学中有心力包括万有引力，重力，静电力，部分磁场力等［2］。通过有心力理论分析质点的运动状况，在天体研究、原子结构与核力研究、太空安全和相关技术发展、先进通讯、地球资源探测和军事侦探等方面具有重要的意义［3］。有心力是理论力学教学中的重要内容。在教学实践中，常见的有心力实例如天体间万有引力和电子受库仑力作用在原子核内的运动，无合适的实验和教具展示，学生难以建立物理直观图像，难以深刻理解有关内容。本文研究运用Mathematica进行编程，直观、清晰地展示有心力下物体的运动，以此辅助理论力学教学。Mathematica［4］是美国Wolfram Research公司开发的数学软件，功能强大，使用方便，能进行微分、积分、微分方程式求解等运算。其内置了大量而丰富的内部数据处理函数，仅仅需要简单的命令就可以计算函数和绘制图形。Mathematica还可进行人机交互，通过简单的命令即时显现图像和数值的变化，动态地展现物理图像随物理参数变化效果。此外，Mathematica平台在互联网上分享很多专业程序包和演示项目。理论力学问题通常涉及复杂的高等数学计算，运用Mathematica辅助理论力学研究有助于提高物理教学效果。Mathematica展示动画是基于科学公式计算的，与Flash等动画制作软件相比更加科学准确。本文研究利用Mathematica软件探究有心力作用下质点运动规律，绘制运动图线，展示质点在有心力下的运动过程，优化教学设计，有利于学生建立物理情景，加深对物理概念和规律的认识。

1 平方反比引力下质点运动的轨道

通过推导可知，在平方反比引力作用下质点的运动轨迹相应方程是

这是极坐标下典型的圆锥曲线方程［1］。在实际教学中，多数学生对极坐标方程和曲线图形理解困难。通过Mathematica内置的极坐标画图函数PolarPlot和可视交互命令Manipulate，绘制随着离心率e的不同而变化的圆锥曲线。在式(1)中，设p=1，拖动参数滑动块，改变离心率e值，Mathematica可及时、动态地展示圆锥曲线相应不同离心率的图线，展现了图像动态变化的效果，有助于学生理解有关内容。在Mathematica工作窗口输入 Manipulate［PolarPlot［1/(1+e*cos［t］)，{t，0，2Pi}，{e，0，2}］，移动滑块，改变 e 值，得到图形如图 1所示。

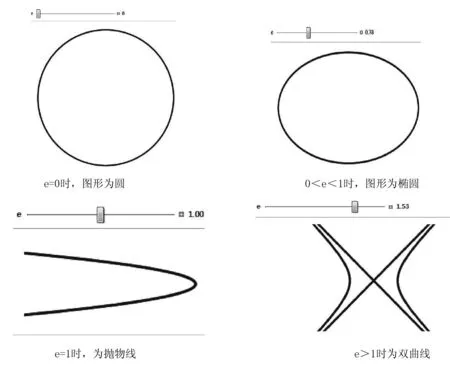
图1 随离心率e的变化，圆锥曲线的变化

2 开普勒定律和两体运动的Mathematica模拟

图2 开普勒第二定律的计算机模拟

在很多力学教材中，开普勒定律和两体问题是有心力教学中的重要内容。由于缺乏合适的展示教具，很多教师在实际教学中只注重开普勒的定律公式的推导及物理定理的证明。运用Mathematica进行有关的动画制作和展示，有助于学生对这一知识点的掌握。此处，运用Mathematica网络资源平台分享的开普勒第二定律演示动画，图2为相应于离心率0.86和0.5时，在不同时间段内太阳和运动着的行星的连线扫过的面积示意图。在远日点附近相对引力小，行星加速度小，单位时间转过的角度小，但是由于与力心连线的距离远扫过的面积并不小;在近日点附近，质点运动速度快，单位时间连线扫过的角度大。虽然行星在不同区域运动时单位时间内转过角度不同，但是正是在有心力作用下，太阳和运动着的行星的连线所扫过的面积都是相等的。此外，借助Mathematica还可以方便地改变行星运动轨道的离心率，形象地展示不同离心率下开普勒第二定律是普遍适用的。

选取一固定参考系，由开普勒第一定律可知，行星围绕着太阳做椭圆运动，由开普勒第三定律的修正，太阳也围绕着行星做椭圆运动，这就构成两体运动问题。两体的质量不同，离心力不同，运动轨道的形状就有差异。从理论上分析，质量大的物体轨道小，质点小的物体运动轨道大。若离心率不同，运动的轨道难以想象，抽象程度高。由Mathematica自定义函数，利用如上开普勒三大定律定义 r［ε_，θ_］:=5/(1+εcos［θ－π/4］))，即r为ε和θ的函数，x，y也为ε和θ的函数，对其编程操作，不仅能能够展现出不同离心率的运动轨道图样，还能控制物体的运动，展现不同质量比和不同离心率的运动图景。图3中，当物体质量比为1，离心率为0时，其两物体相向运动，运动在同一条轨道上。当质量相同时，物体轨道也相同。但离心率为0.5，绕两轨道中心做椭圆运动。

图3 质量相同离心率不同时两体运动轨道的对比

图4 质量比较小时，离心率不同的两体运动的对比

当物体质量比不同时，运动轨道大小不同，且离心率不同，轨道大小也不同，如图4所示。质量比大时，大质量物体几乎不运动，质量小的物体轨道变化较大变化。如图5所示，大质量物体没有显示运动轨道。

在图像变化中小物体离质量大的物体较近时运动速度快，较远时运动速度慢，符合开普勒第二定律。通过演示，让学生的理论分析得到证实，验证了开普勒第二定律的正确性和合理性。此外，还可以指导学生探究质量比小于1的两体运动规律、离心率大于一的两体运动规律等。

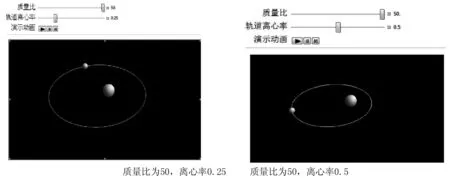
图5 质量比较大时，离心率不同的两体运动的对比

3 任意幂有心力问题的探讨与研究

一般来说，有心力与距离呈幂指数的形式为

质点在有心力的作用下的有心运动属于非线性动力学问题，对其问题求解需要用更复杂的数学，理论分析较麻烦。在Mathematica中，用数值模拟，可以任意选择每一个质点的初始条件:质点的位矢初始坐标r0(x0，y0)和初始速度v0(v0x，v0y)，质点运动的轨迹一般是不闭合的，轨道离力心最远点或最近的点叫做拱点，两相邻拱点矢径间的夹角称为拱角［1］。利用Mathematica互联网平台上分享的展示项目，A=5，x0=－0.62，y0= －0.84，v0x=0.75，v0y= －0.66，在一定的时间内显示，设 t0为单位时间，当 n=1，n=2 时，相应有心力作用下质点的运动轨迹。

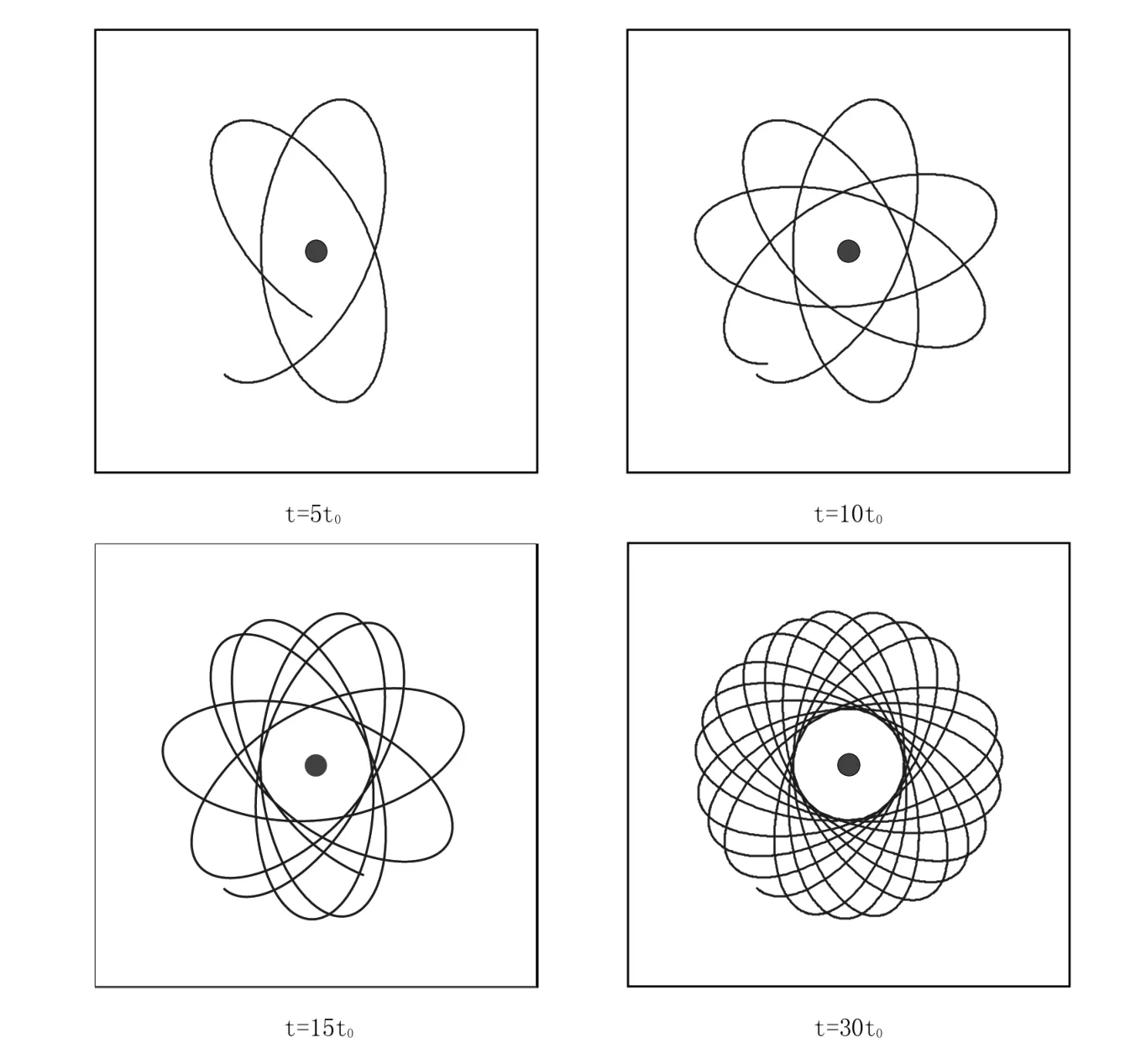
图6 n=1 质点随时间的运动轨迹

图7 n=2 质点随时间的运动轨迹

当n=1时，质点运动轨道如图6所示，轨道为不闭合曲线，质点在30个单位时间运动的过程。我们可以观察质点一方面绕力心运动，同时轨道本身还绕力心转动，轨道绕力心转动称为轨道的进动［1］。当n=2时，质点运动轨道如图7所示，此运动图象较简单，且运动图像是一个闭合的图像，在2个单位时间内已闭合。当n不同，质点的运动轨道不同，运动图像差异较大。通过Mathematica也可以探究n=3，4，5等时物体的运动规律，由此激发学生对有心力规律的探究和学习动力。