高职院校数学课程教学内容整合初探
2014-12-28邓瑞娟姚小菊黄家云
邓瑞娟,姚小菊,黄家云
(芜湖职业技术学院基础部,安徽芜湖241006)
1 数学课程面临的现状
(1)招生规模不断扩大。通过对全国历年参加高考人数和录取人数的统计对比发现,我国的高等教育已经进入了一个数量上高速增长的时期(表1)。

表1 1977-2012年高考相关信息对比表
(2)学生数学基础总体较好,但差异较大。近年来,随着高考制度的不断完善,高职院校招生呈现出多元化的特点,既有普高学生,也有对口学生,还有自主招生的学生。同时,自主招生的学生数量正在逐年增加,涉及的专业也越来越多。这也导致了学生的数学基础总体较好,但差异较大的现状,给教师的教学带来很大困难。为了解决这些困难,很多院校根据目前的形势进行了相应的教学改革,也总结了例如案例驱动法、分层教学法、订单式教学法等新颖的教学方法,均收到了较好的教学效果,但这些改革主要集中在教学方法上,没有从根本上解决问题[1]。
2 教学内容改革中有待解决的问题
(1)教学内容过于理论化。在目前的数学课堂上,教师主要讲解概念、推导定理,过于强调对学生求解习题的方法和技巧的训练,忽视了对学生运用数学解决实际问题能力的培养,这就导致一部分学生形成了数学“枯燥”、“无用”的观点,学习数学的积极性不高,造成了数学“难学难教”的现状。
(2)教学手段相对落后。计算机技术和网络技术的日益发展,深刻地影响着当代大学生的学习和生活。目前,绝大多数高职院校的数学教师仍采用传统的黑板教学,即使有教师使用多媒体,也基本是简单的替代板书内容,总体来说,数学课程授课并没有充分发挥现代教育手段的优越性[2]。
(3)数学课程与专业课程脱节。数学课程的教学内容中并没有很好地体现其在专业课上的应用,这就使得学生很难了解高等数学与本专业之间的联系,认为数学课完全是一门孤立的基础课,对其重要性认识不够。可以说,传统的数学课程教学与专业课程教学比较脱节,没有有机地结合起来[3]。
3 教学内容改革构想
对教学内容改革的宗旨是:使数学课程能为学生学习后继课程(基础性)、解决实际问题(工具性)、发展理性思维能力(思维训练)、提高自学科学技术的能力(可持续发展)提供必不可少的数学基础知识、数学方法以及必要的数学训练。现以芜湖某高校为例,介绍教学内容改革的基本构想。
3.1 将教学内容模块化
高职院校的很多专业都开设了数学课程,但开设数学课程的学时、内容都有所不同。比如:电气类专业所需数学知识较多,因此在大一、大二期间分别开设“高等数学”、“工程数学”,机械类专业根据具体需求,为不同专业开设“高等数学”、“工程计算”两门课程等。因此,在设计教学内容时,可以选取专业课程中常用的数学基础知识,在保证科学性和保持衔接性的前提下,将教学内容整合成相对独立的模块。在设置教学内容时,可以设置一些基本模块,然后再根据每个系不同的专业需求、不同学时以及学生不同的基础,选择所需的模块以及模块的难度。具体模块划分见表2。
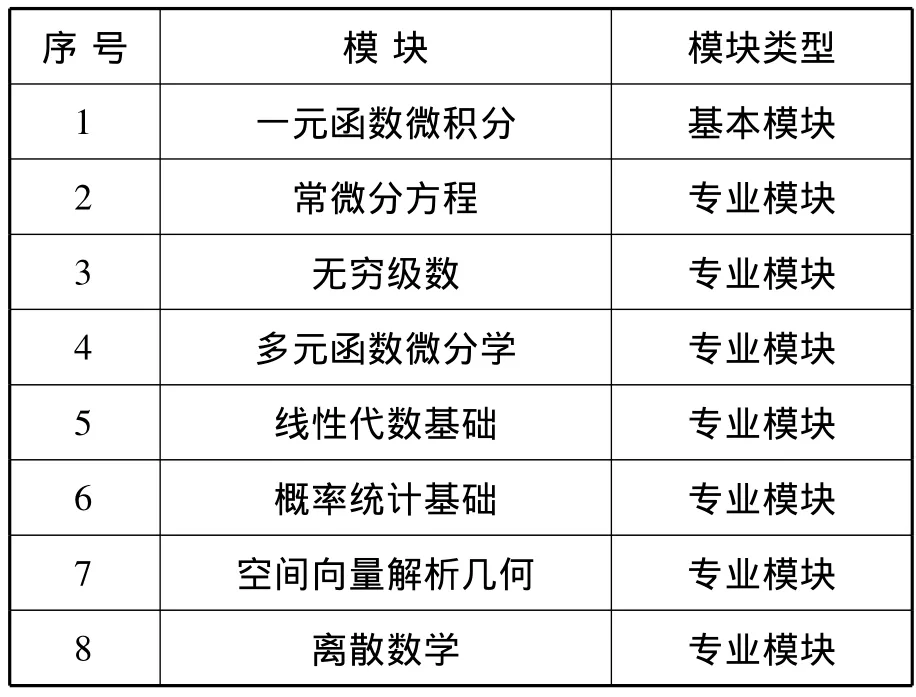
表2 课程模块划分图
通过走访专业课程教师、参加培训班、外出调研、学习其他学校的先进做法、听取学生对高等数学课程的看法等多种途径,广泛收集相关信息,针对不同专业量身选择相应的模块。以电气类电气自动化专业为例,大一期间开设124学时的数学课程,将学习一元函数微积分、常微分方程、无穷级数、多元函数微分学等四大模块;大二期间开设54学时的数学课程,学习线性代数基础、概率统计基础等两大模块。再如信息工程系的各专业学生在后继课程学习过程中对数学知识的需求与其他专业有很大不同,在大一期间的前56学时主要学习一元函数微积分模块,后72学时主要学习线性代数基础与离散数学两大模块。在以上八大模块中,每一模块的具体内容也分为掌握、理解和了解3个层次。如在一元函数的积分学中第二类换元积分法有简单根式代换、三角代换及倒代换三种,可将简单根式代换作为必掌握内容,将三角代换作为需要理解的内容,将倒代换作为选学内容,在分班之初,可通过入学摸底考试,在同专业内将程度接近的学生分在一个教学班里,教师在授课过程中根据专业需求及班级学生的具体情况选择相应难度。
3.2 将数学建模的思想融入高等数学的教学过程
数学建模是通过建立数学模型来解决实际问题的方法,是数学应用性的体现,也是数学区别于其他学科的重要方面。它注重人们在解决实际问题中去伪存真、从现象中抽象出本质的过程。在数学课程的教学过程中融入建模思想:(1)能够了解数学知识在生活中的具体应用;(2)能够培养学生学习数学的兴趣,调动学生的学习积极性;(3)能够训练学生通过各种渠道搜集资料、整理资料的能力;(4)能够提高学生逻辑思维的严密性;(5)能够提升学生运用数学知识解决复杂现实问题的能力。因此,数学教师可在课堂教学过程中适当地引入数学建模,帮助学生加深对相关概念的理解。
3.3 教学内容与专业紧密结合
这里的紧密结合不只是在教学模块的选择上以专业需求为基本原则,还可以在教学过程中引入专业课程的相关例题,学生要完成这些题目,除了要有必要的数学知识,还要运用专业课程中的知识,从而从根本上解决部分学生“数学学不学无所谓”的不正确的思想。比如,在给电气类相关专业学生讲授“导数的概念”时,可以用电学中的相关知识点举例;在给信息系相关专业学生讲解离散数学模块的“有向图的连通性”时,可用操作系统中“死锁”这一知识点举例。
3.4 教学过程中引入数学软件
数学给人以“难学难教”的印象,主要是由于传统教学流程重点是计算,忽略对数学思想的理解,具体见图1。

图1 传统教学流程
实际上,学生对数学概念的深刻理解才是其应用数学的基本前提。因此,在数学课程教学内容的改革过程中,应注意弱化复杂定理的证明、推导过程,降低对复杂计算的要求。为了弥补由此带来的一些弊端,可在教学内容中适当引入Mathematica、MATLAB等数学软件,培养学生运用软件解决复杂计算的能力[4]。这样可以将教师从讲解复杂计算中解放出来,争取更多时间为学生讲解数学概念、数学思想以及数学的应用(图2)。
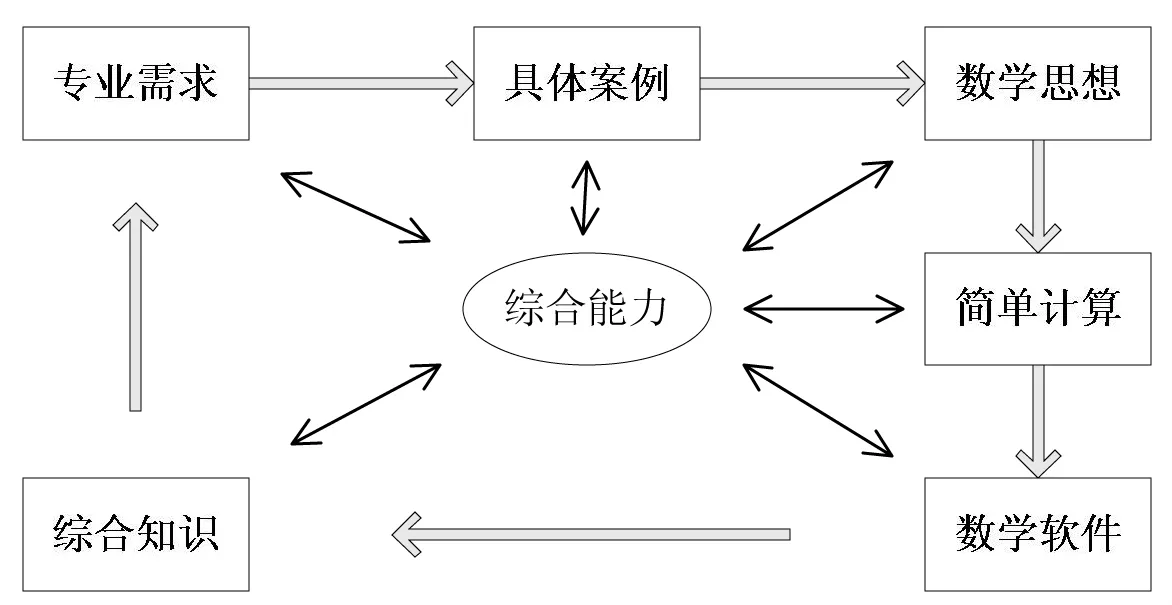
图2 现代教学流程
引入Mathematica、MATLAB等数学软件,有助于学生对数学中一些抽象的理解。例如,在介绍一元函数极值时,已知函数单调性的分界点是函数的极值点,但是反之不成立。然而很多学生都认为函数的极值点必然是函数单调性的分界点。为了解除学生对这一问题的误区,可运用 Mathematica绘制函数 f(x)=的图像,直观给出x=0附近的情形加以说明。具体程序如下:
f[x_]:=x^4+x^2*(sin[1/x])^2/;x≠0
f[x_]:=0/;x=0
Plot[f[x],{x,= - -01.,0.1}]
从图3中可看出x=0为函数的极小值,但在该点附近函数处于振荡状态,不是单调性的分界点。
3.5 用图形、数据代替复杂证明
加强传统数学内容与图形、数值的结合,可以实现数学课程“教得来,学得下,用得上”的基本目标,达到“实用、够用”的根本目的。
对数学课程教学内容进行改革,是希望提高学生在学习过程中的积极性、主动性。在课程内容改革的同时,可以加强教材建设,并在教材的实际使用过程中完善内容的编排,真正形成适合高职学生的数学教材;另外,也可对数学课程现有的评价体系进行思考,设计出更合理的评价模式。
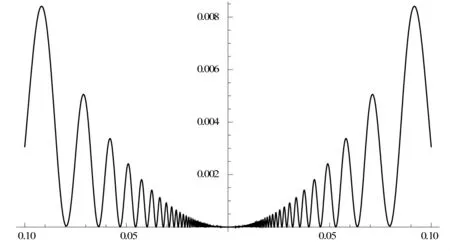
图3 f(x)函数图形

图4 y=sinx函数图形x
[1]周光亚.高职数学课程改革研究与实践——植入数学软件,构建新型高职数学课程教学体系[J].四川工程职业技术学院学报,2010,24(2):78 -81.
[2]王国强,岳玉静,蔡新中,等.浅议高职数学课程教学的现状及改革策略[J].上海工程技术大学教育研究,2011(1):56-61.
[3]马素萍.论服务于专业教育的高职数学教学改革途径[J].湖北广播电视大学学报,2013,33(3):38-39.
[4]肖庆丰.浅析高职数学课程的结构与内容改革[J].价值工程,2012(9):189.
