一种轴对称平面反射阵天线的布阵方法

（北京空间飞行器总体设计部，北京 100094）

1 引言

近年来随着航空航天技术的发展，卫星微波通信系统对高增益、低剖面，具有良好扫描特性的天线需求日益增大。抛物面天线由于其高增益、高效率的特性，最近几十年在卫星通信系统、雷达系统以及深空探测领域得到广泛的应用。然而，由于抛物面天线自身的结构特点，其存在加工难度大，不易与航天器共形，制造成本高等问题。

平面反射阵列天线是用平面反射面来代替抛物面的一种新型反射阵列天线，这种天线由于其剖面低、质量小、价格低、易加工、易共形等优点，被越来越多地应用于各种雷达天线系统中。然而，对于传统的方形栅格布阵方式，须求出每个振子单元的相位，通过相位反推出振子的尺寸，这就需要庞大的计算量，而且对每个振子的加工精度有着严格的要求，振子单元加工精度的不一致会导致平面反射阵列天线的带宽较窄。目前，国内外平面反射阵列天线研究重点在于阵面辐射单元设计，根据要求选用不同的辐射单元形式，分别提出了矩形贴片、环形贴片、风车型贴片、空气层贴片、环圆混合型贴片等多种辐射单元形式［1-7］，布阵方式都采用方形栅格型布阵，这种布阵方式的平面反射阵天线设计初期计算量庞大，且带宽较窄。

针对这一问题，本文首先介绍了菲涅尔原理布阵方法，进而提出一种新的适用于轴对称平面反射阵天线的布阵方法，并对其进行了仿真验证，该方法大大减少了平面反射阵列天线设计初期由于各单元相位差异而造成的庞大计算量，可应用于星载轴对称平面反射阵天线设计。

2 菲涅尔原理布阵方法

传统平面反射阵列天线一般都是方形栅格布阵方式，这种布阵方式需对反射面上的每一个振子单元分别设计，设计过程较为复杂繁琐。而基于菲涅尔原理布阵的平面反射阵列天线采用“环型带状”布阵，即每一环带上的贴片相同，每一环带上的贴片只需设计一次即可，这样就减少了计算量，提高了工作效率，同时也能保证每一环带贴片加工一致性［8］。

对于任何平面反射阵列天线，要实现远场平面波阵面，必须通过调节每个辐射振子的相位来补偿由于馈源到振子不同距离所造成的相位差。对于基于菲涅尔原理布阵的平面反射阵列天线，其相位调节通过一个个环带来实现，每个环带可以实现任何相位，环带种类的多少主要取决于所需调节相位的精度，即菲涅尔带相位调节效率［9］

式中：φ为每一环带的相位调节增加量；φ＝2π／P，P为环带种数。可见环带种数越多精度越高，即相位补偿效率越高，天线的效率越高，为验证该布阵方法的有效性，本文设计了4种环带的平面反射阵天线，即P＝4，由式（1）可得，此天线的相位调节效率可达81%。

如图1所示，假设n为菲涅尔环带的个数，第n个环带的内外环半径分别为rn和rn＋1，第n个环带所调节的相位为360n／P，根据经典菲涅尔公式［9］

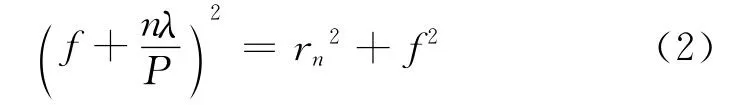
可得

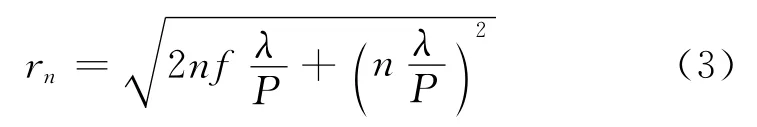
式中：λ为入射波波长；f为焦距。由式（3）求得每个环带的大小，再根据每个环带所需的相位调节来设计所需贴片大小和种类。

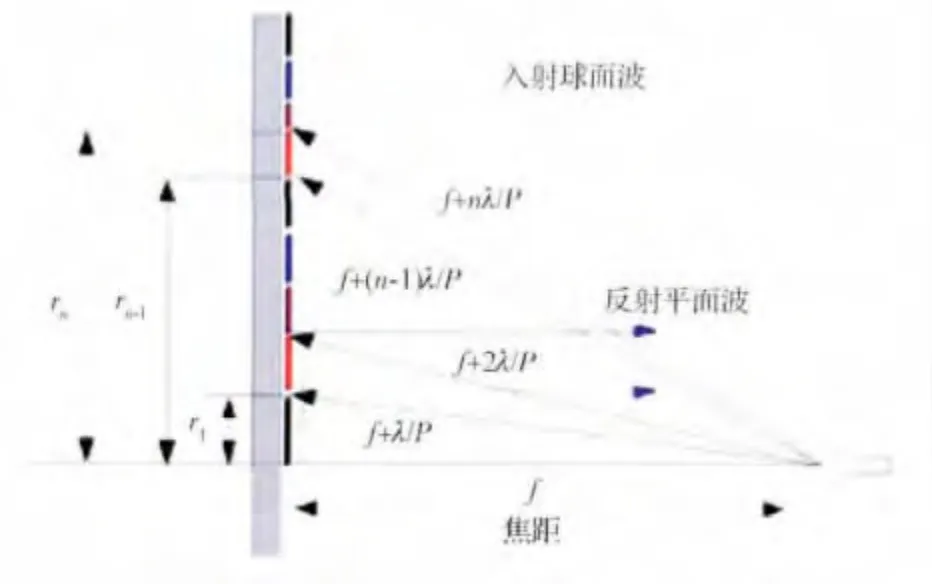
图1 菲涅尔反射原理几何示意图Fig.1 Fresnel reflector：geometry and notation

对于菲涅尔布阵的平面反射阵天线，每个环带上的贴片辐射相位是一致的。当馈电喇叭的辐射场照射在每个贴片上时，谐振电场将在微带贴片中传输，被贴片的开路或短路的终端反射回来，形成驻波，由于贴片自身存在阻抗，所以驻波和贴片阻抗共同作用使得入射电磁波带着φ的相位变化重新辐射回空中，所有的贴片相当于再辐射器。贴片的阻抗与贴片的尺寸有关，可以通过改变贴片的尺寸来实现贴片阻抗的变化，最终改变再辐射电场的相位φ。

假设入射电场为

式中：E0表示入射电场的幅度，x、y、z表示在直角坐标系的坐标，ui和vi表示入射方向角度数值，式（5）给出了极坐标下入射电磁波的方向。

式中：θi、φi表示极坐标下电磁波的入射角度。

若只考虑接地板的影响，那么经地板反射后的电场可表示为

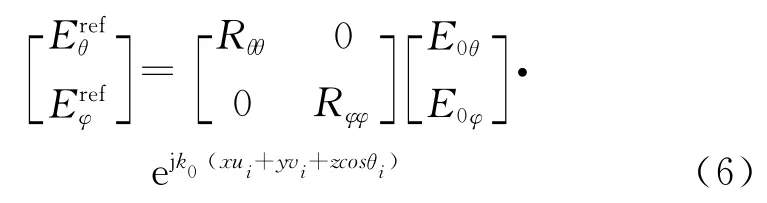
式中：Rθθ和Rφφ分别是平面波反射系数；E0θ、E0φ表示入射电场在θ、φ方向的幅值。经计算

式中：k0表示中心频点对应的波数；d为单元间距。这里

式中：εr为平面反射阵介质板介电常数。

若考虑到微带贴片的影响，那么经贴片散射后的电场可表示为

式中：Sθθ、Sθφ、Sφθ和Sφφ分别是平面波散射系数，它们与贴片的种类和尺寸有关。

由式（9）可知微带平面反射阵列天线的远区电场可表示为

式中：Rtot为散射与反射矩阵，Rtot＝r为对应位置的极坐标；N为贴片个数，由式（10）即可求得贴片再辐射电场。

综上所述，对于基于菲涅尔原理布阵的平面反射阵天线，通过辐射贴片实现每个菲涅尔相位环带的相位补偿。设计方法可以归纳为以下3点：

（1）根据要求确定所需相位环带种数P，环带种数P主要影响天线相位补偿效率，环带数越多天线布阵越密，天线的辐射效率越高；

（2）根据式（3），求得每一个相位环带对应的内外环半径，内外环半径差值即为所需贴片原始周期尺寸，根据环带补偿相位和贴片原始周期尺寸选取合适种类的贴片单元；

（3）通过等效波导单元模型法［10］计算出贴片尺寸与相位之间的关系，选取合适的贴片尺寸完成整个天线布阵设计，通过式（10）可以求出天线的远场辐射特性。

3 天线设计与验证

本文提出的基于菲涅尔原理布阵的平面反射阵列天线与传统平面反射阵列天线很类似，设计方法基本一致。为验证该布阵方法的有效性，本文所用贴片振子为环圆混合型贴片，通过改变内圆贴片的半径大小来实现相位的调节。如图2所示，环圆混合型贴片的环形贴片尺寸不变，外环半径固定为0.7mm，内环半径固定为0.6mm，只通过改变环内圆型贴片半径来实现相位变化，内圆半径变化范围为0.05～0.6mm。

出于对介质机械强度、环境性能、成本费用等方面的考虑，本文的微带阵列介质选用罗杰斯板材，型号Rogers 5880，其εr＝2.2，损耗正切角为0.000 9，介质厚度约为介质波长的1／4，即为0.538 mm，这样通过加金属环带贴片和不加金属环带贴片构成0°和180°相位补偿带，再设计90°和270°环带上的贴片即可构成4 个相位补偿环带。由于环带大小不同，所以不同种类环带上的贴片间距不同，故不能单纯地固定贴片周期尺寸。首先假定贴片初始间距为1.8mm，经计算可得贴片尺寸与相位之间的关系曲线，如图3所示。

图3 环圆混合型贴片单元的相移曲线Fig.3 Variation of reflection phase for annular patch element

由图3可知，环圆混合型贴片可以实现130°～-160°的相移，相移曲线较为平滑，这里只须找出相移为90°和270°所对应的贴片尺寸即可，设计的菲涅尔天线参数为P＝4，f＝94 GHz，焦距F＝35mm，环带数n＝9，由式（3）可以求得各环带宽度分别为D1＝7.52 mm，D2＝3.17 mm，D3＝2.47 mm，D4＝2.12 mm，D5＝1.9 mm，D6＝1.74mm，D7＝1.63 mm，D8＝1.53 mm，D9＝1.46mm。那么可以定义90°环带上贴片间距分别为＝3.17／2＝1.585mm，＝1.74mm；定义270°环带上贴片间距分别为＝2.12mm，＝1.53mm。根据不同的贴片间距，利用等效波导单元模型法即可求得所需相移对应的贴片大小，再经过合理布阵最终完成整个天线阵的设计。

通过上面计算，设计了直径为40mm，环带数n＝9，焦距F＝35mm 的菲涅尔布阵方式的平面反射阵列天线，工作频率为94GHz，开口波导WR-10作为馈源，采用HFSS软件进行仿真运算。

工作频率为94GHz，菲涅尔平面反射阵列天线反射面结构示意见图4。

图4 菲涅尔布阵平面反射阵列天线反射面顶视图Fig.4 Top view of the Fresnel zone plate reflectarray antenna

图5为设计天线的0°面和90°面辐射方向图，已考虑馈源遮挡情况，如图6所示，该设计方案0°面和90°面有着很好的方向性，辐射方向与设计要求相吻合，归一化后，副瓣电平低于-20dB，交叉极化度也都小于-20dB。

图6为设计天线增益与工作频率的关系曲线，由图6可知，与传统平面反射阵列天线带宽相比，该天线带宽较宽，其1dB带宽约为15%。

该天线在中心频点94 GHz时的最大增益约28.6dB，辐射效率约46.7%，辐射效率偏低主要是受馈源辐射特性、馈源遮挡及相位补偿效率等因素影响。为提高天线辐射效率，首先需要选取合适的馈源。为了使反射面得到最大的口径效率，要求馈源方向图和反射面张角配合，尽可能减少越过反射面边缘的能量漏失，使天线增益因数最大。同时馈源方向图接近于圆对称，副瓣和后瓣也应尽可能的小，馈源要宽频带及尽可能低的交叉极化电平，一般选用圆锥波纹喇叭作为馈源。其次要提高反射面的相位补偿效率。根据式（1），相位补偿效率与菲涅尔相位环带种数有关，本文选用的4相位环带方案，相位补偿效率为81%，而8相位环带的相位补偿效率可以达到95%，所以为提高天线效率可以选择高的相位环带种数。

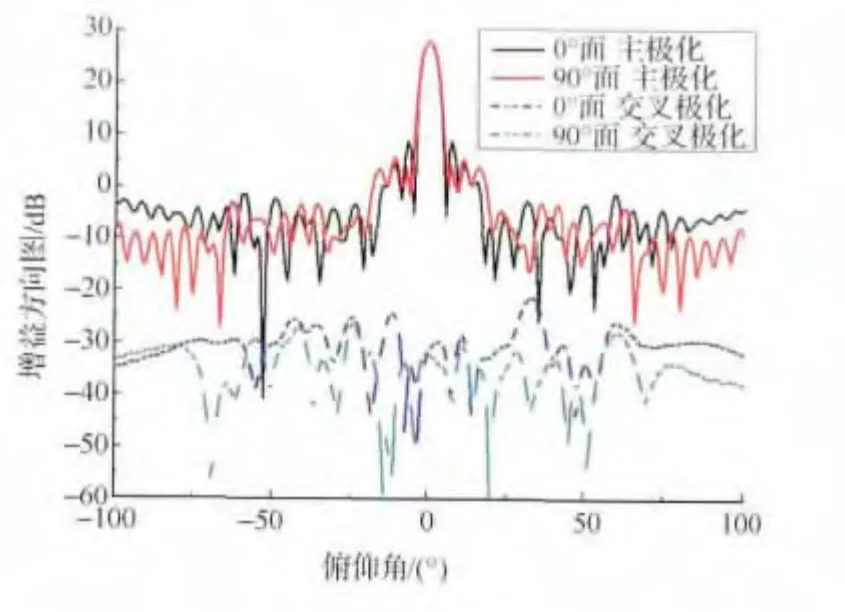
图5 菲涅尔平面反射阵列天线正馈辐射方向图Fig.5 Calculated radiation patterns of the Fresnel zone plate reflectarray antenna

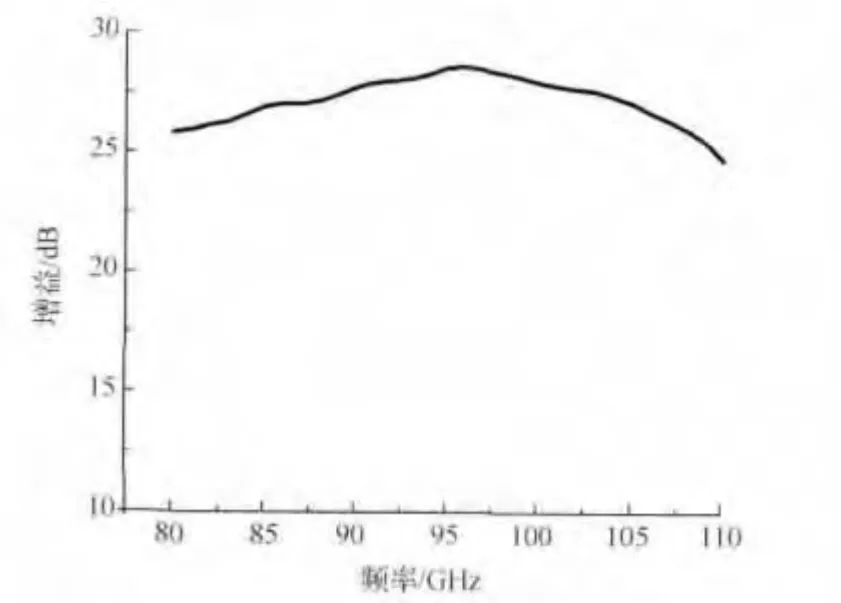
图6 增益与频率曲线Fig.6 Gain vs.frequency for reflectarray antenna

4 结束语

本文针对星载平面反射阵列天线设计过程须耗费庞大计算量的缺陷，提出了一种基于菲涅尔原理的新型毫米波轴对称平面反射阵列天线布阵方法，该方法大大减少了平面反射阵布阵须耗费的庞大计算量。在此基础上设计了工作频率为94GHz，由4种菲涅尔相位环带组成的平面反射阵列天线，仿真结果表明：天线副瓣低于-20dB，1dB 带宽约为15%，为星载单层轴对称毫米波平面反射阵列天线的设计提供了一种新的途径。

（References）

［1］R Leberer，W Menzel.A dual planar reflectarray with synthesized phase and amplitude distribution［J］.IEEE Trans.Antennas Propagat，2005，53（11）：3534-3539

［2］A Encinar.Design of two-layer printed reflectarrays using patches of variable size［J］.IEEE Translated Antennas Propagat，2001，49（10）：1403-1410

［3］H L Bing，Z Wang，P Du.Novel broadband reflectarray antenna with windmill-shaped elements for millimeterwave application［J］.International Journal of Infrared and Millimeter Waves，2007，28（5）：339-344

［4］L Li，Q Chen，Q W Yuan，et al.Novel broadband planar reflectarray with parasitic dipoles for wireless communication applications［J］.IEEE Antenna and Wireless Propag，2009，8：881-885

［5］M E Bialkowski，A W Robinson，H J Song.Design，development and testing of X-band amplifying reflectarrays［J］.IEEE Translated Antennas Propagat，2002，50（8）：1065-1076

［6］Tian X Wang，Zhong Q Xue，Kun P Liu.Novel broadband reflectarray antenna with two-type elements for millimeter-wave application［J］.International Journal of Infrared and Millimeter Waves，2010，31（7）：833-839

［7］王云秀，王秉中，李华，等.平面反射阵列天线的研究进展［J］.系统工程与电子技术，2008，30（2）：388-392 Wang Yunxiu，Wang Bingzhong，Li Hua，et al.Advances on the research of planar reflectarray antennas［J］.Systems Engineering and Electronics，2008，30（2）：388-392（in Chinese）

［8］L C J Baggen，M H A J Herben.Design procedure for a Fresnel-zone plate antenna［J］.International Journal of Infrared and Millimeter Waves，1993，14（6）：1341-1352

［9］H D Hristov，M H A Herben.Millimeter-wave fresnel zone plate lens and antenna［J］.IEEE Translated Antennas Propagat，1995，43：2779-2785

［10］Feng Chi E Tsai，Marek E Bialkowski.Designing a 161-element Ku-band microstrip reflectarray of variable size patches using an equivalent unit cell waveguide approach［J］.IEEE Translated Antennas Propagat，2003，51（10）：2953-2962