福寿林场杉木人工林不同林龄直径结构研究

周永奇，李际平，曹小玉

（中南林业科技大学 林学院，湖南 长沙 410004）

福寿林场杉木人工林不同林龄直径结构研究

周永奇，李际平，曹小玉

（中南林业科技大学 林学院，湖南 长沙 410004）

以福寿林场杉木人工林为研究对象，利用正态分布、Weibull分布、对数正态分布、Gamma分布4种分布函数分别对3个林龄9块样地的直径分布进行了拟合研究。结果表明：偏度系数均为正值，直径分布偏向中小径阶，6年生杉木偏度最大，13年生偏度最小。峰度系数6年生杉木均为正值，直径分布较集中，13年生、20年生杉木大都为负值，直径分布较离散。6年生杉木用对数正态分布和Gamma分布拟合效果好，13年生杉木用Weibull分布拟合效果好，20年生杉木拟合效果均不理想。

杉木人工林；直径分布；分布函数；林龄

森林作为陆地生态系统的主体，它在满足人类生存和发展物质产品及环境服务中有着不可替代的作用[1]。合理的林分结构是森林发挥功能的前提。林分直径分布[2-4]是指在林分内各种直径大小的林木按径阶的分配状态，它是准确评价营林措施的基础，影响林木的基本因子，如树高、形数、材积、冠幅等等。研究林分直径分布规律对编制森林经营方案，预估林分生长和收获模型有重要意义[5]。

林分直径结构的研究已有近百年的历史，一直以来都是林业领域研究的热点和难点问题。初期主要运用列点法和林分表法研究，随着计算机技术的发展，近些年来主要运用分布函数法对分布概率曲线进行拟合[6-7]。应用较多的直径分布模型有正态分布、Weibull分布、负指数分布、β分布、对数正态分布[8]等等，对于不同的林分结构，各模型的拟合效果也不尽相同。目前，关于林分直径分布规律的研究较多，但普遍都是对相似年龄段静态下的直径结构进行研究，对不同林龄的直径结构动态研究相对较少。本文结合福寿林场杉木Cunninghamia lanceolata林分直径结构特征，选取4种分布函数分别对6年、13年、20年的杉木林分直径分布进行了研究，为合理调整福寿林场杉木林分结构，制定经营管理措施提供有效的参考依据。

1 研究区概况

福寿林场位于湖南省岳阳市平江县福寿山上， 地 处 28°3′00″～ 28°32′30″N， 113°41′15″～113°45′00″E，北连思村级尚山村，南抵浏阳市。东西长达13 km，形似“展翅蝙蝠”。林场地处罗霄山脉连云山支脉，地势南高北低，最高峰海拔1 573.2 m，最低处为湖口峡底，海拔835 m，林场场部海拔1 078 m。属湿润的大陆性季风气候。年平均气温12.1℃，年相对湿度87%。场内海拔800 m以下的土壤为山地黄壤；800～1 400 m为山地黄棕壤。整个林场植物种类250余种。

2 材料与方法

2.1 实验材料

2012年8月，在福寿林场选取有代表性的杉木人工林地段，设置9块样地，林龄分别为6、13、20年，每个林龄各3块样地，样地大小为20 m×30 m，对样地内所有乔木进行每木检尺，同时，记录林下植被状况，环境立地因子等。各样地基本信息见表1。

表1 样地基本概况Table 1 Basic condition of sample plots

2.2 研究方法

用来拟合林分直径分布的函数较多，结合众多学者的研究结果[9-12]及福寿林场杉木人工林林分结构特征，本研究选择正态分布、Weibull分布、对数正态分布和Gamma分布4种分布函数对其进行分布拟合，6年生杉木按1 cm径阶整化，13年生和20年生杉木按2 cm径阶整化，分别统计样地内不同径阶的株数，计算直径标准差、偏度系数和峰度系数，拟合效果用χ2检验法对其进行检验[13-14]。

2.2.1 偏度与峰度

偏度是体现分布对称、偏离程度的指标，偏度为正值表示左偏，均值在大于峰值的一边，偏度为负值表示右偏，均值在小于峰值的一边，偏度的绝对值越大则偏离程度越大。峰度是体现离散程度，曲线陡峭程度的指标，峰度为正值表示直径分布较集中，为尖峰态，峰度为负值表示直径分布较分散，为低峰态。偏度系数α和峰度系数β的计算公式分别为：

式中，v3表示3阶的中心距，v4表示4阶的中心距，σ表示直径标准差。

2.2.2 正态分布

正态分布的概率密度计算公式为：

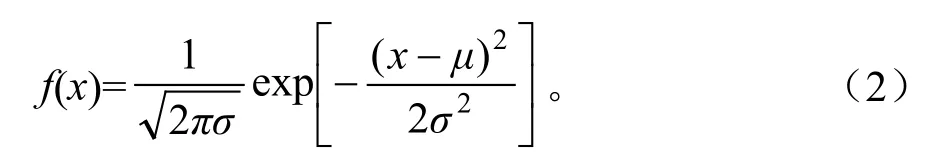
式中，μ表示x的数学期望，σ表示林分直径标准差。

2.2.3 Weibull分布

Weibull分布的概率密度计算公式为：

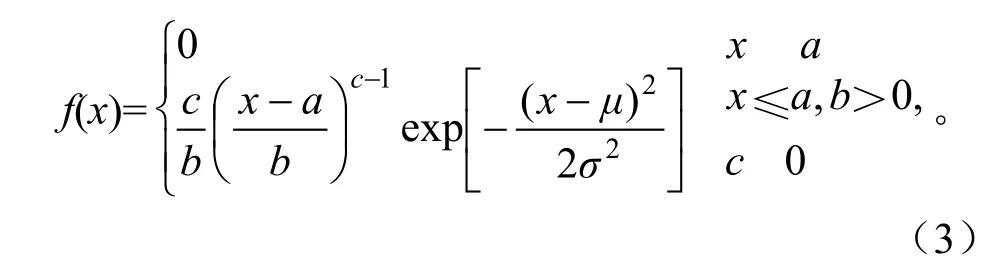
式中，a为位置参数，一般定为林分直径最小径阶的下限值，b为尺度参数，c为形状参数。

2.2.4 对数正态分布

对数正态分布的概率密度计算公式为：

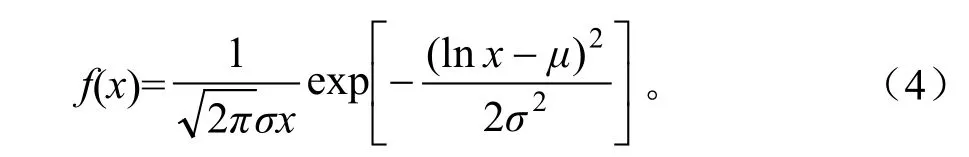
式中，μ表示变量lnx的数学期望，σ表示随机变量lnx的标准差。

2.2.5 Gamma分布

Gamma分布的概率密度计算公式为：

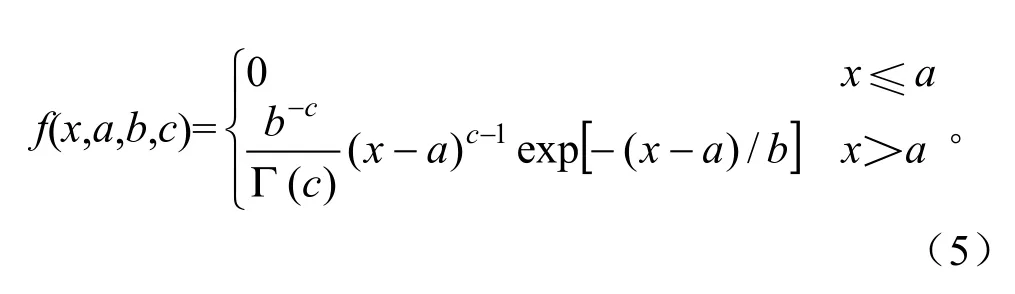
式中，a为x的可能最小值，b为尺度参数，c为形状参数。

2.2.6 分布检验

用χ2检验法在0.05水平下，对直径分布的拟合结果进行检验，检验公式为：

式中，Ni表示第i径阶的实际株数，Mi表示第i径阶的理论株数，n表示径阶数目。

3 结果与分析

3.1 林分直径结构特征值

依据直径分布特征值计算公式，通过Forstat软件求得各样地直径分布特征值，结果见表2。

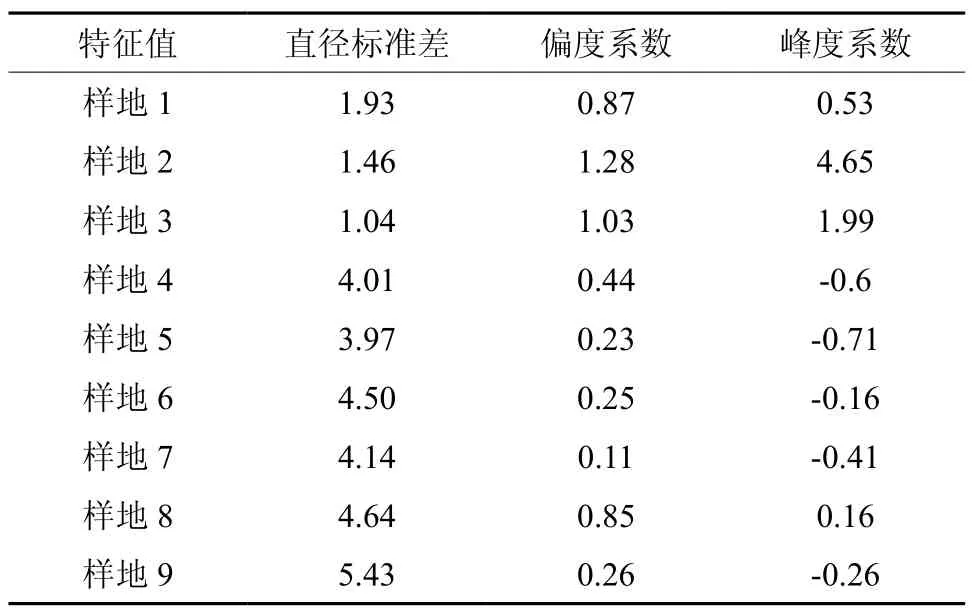
表2 各样地直径分布特征值Table 2 Characteristic values of diameter distribution of plots

由表2可知，6年生杉木的3块样地直径标准差都在1～2之间，直径变动较小。从偏度系数看，偏度系数均为正值，说明直径分布曲线均为左偏，直径偏向小径阶，偏离程度大小为：样地2＞样地3＞样地1。从峰度系数看，峰度系数也均为正值，说明直径分布比较集中，分布曲线比正态分布陡峭，呈尖峰态，其中样地2峰度系数最大，分布曲线最陡峭。

13年生杉木的3块样地直径标准差在3～5之间，直径变动有所增大。从偏度系数看，偏度系数均为正值，直径分布形状呈左偏山状分布，胸径均值在大于峰值的一边，右边有一条长尾，直径分布偏向中小径阶。从峰度系数看，峰度系数均为负值，直径分布比较离散，比正态分布要平坦，呈低峰态，其中样地5分布最离散。

20年生杉木的3块样地直径标准差在4～6之间，直径变动较大。从偏度系数看，偏度系数也均为正值，直径分布为左偏，偏向中小径阶，胸径均值在大于峰值的一边，偏离程度上样地8最大，样地7最小。从峰度系数看，样地7、9峰度系数为负值，直径分布比较离散，分布曲线比正态分布要平缓，呈低峰态，而样地8峰度系数为正值，直径分布相对集中。

从不同林龄的变化情况分析，随着林龄的增大直径标准差依次增大。从偏度系数看，偏度系数都为正值，直径分布曲线为左偏，胸径均值在大于峰值的一边，偏向中小径阶。偏离程度上，6年生杉木最大，13年生最小，基本接近正态分布。从峰度系数看，6年生杉木都为正值，直径分布较集中，呈尖峰态，且峰度系数相对很大，陡峭程度大。13年生和20年生杉木大都为负值，直径分布较离散，比正态分布要平缓，呈低峰态。

3.2 林分直径分布参数估计

本文选用正态分布、Weibull分布、对数正态分布和Gamma分布4种分布函数对直径分布进行拟合，利用Forstat软件求得分布参数的估计值，结果见表3。

由表3可知，各样地Weibull分布函数形状参数c估计值都在1～3.6之间，由尺度参数b可知，1至9块样地中对应直径小于3.9、3.8、2.3、8.3、9.5、10.4、10.7、12.0、12.7 cm的林木株数占相应总株数的百分数约为63%。

3.3 直径分布拟合结果及检验

本文运用χ2检验法在0.05的显著水平下对拟合结果进行检验，若χ2＜χ20.05或P＞0.05则说明在0.05水平下拟合效果显著，否则拟合效果不显著，具体检验结果见表4。同时，对拟合情况进行作图分析，结果见图1。

由表4可知，6年生杉木的3块样地，对数正态分布、Gamma分布、Weibull分布、正态分布对其拟合效果达到显著水平的样地数分别为3块、2块、1块和0块，此外，P越大表明拟合效果越理想，所以，样地3用Gamma分布和对数正态分布模拟效果极好，其中尤以Gamma分布效果最好，总体来看，对6年生杉木直径结构的拟合，对数正态分布和Gamma分布的拟合效果好，Weibull分布的拟合效果一般，正态分布的拟合效果较差。

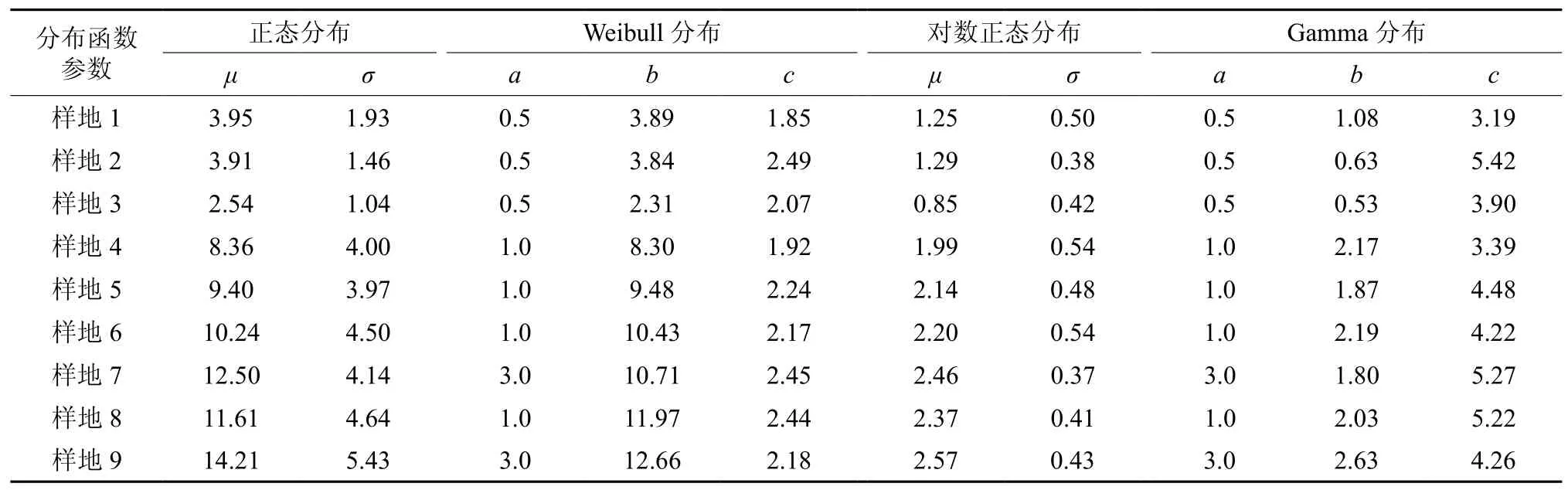
表3 各样地直径分布拟合参数估计值Table 3 Estimated values of diameter distribution fitting for sample plots

表4 直径分布检验结果Table 4 Inspection results of diameter distribution

图1 各样地拟合曲线与实际株数曲线的比较Fig.1 Comparisons of fi tting curves with real ones of distribution functions for sample plots

13年生杉木的3块样地，Weibull分布、Gamma分布、正态分布、对数正态分布对其拟合效果达到显著水平的样地数分别为3块、1块、1块和0块，从P值的大小进一步分析可知，Weibull分布对样地4的拟合效果最好，总体来看，对13年生杉木直径结构的拟合，Weibull分布的拟合效果好，Gamma分布和正态分布的拟合效果一般，对数正态分布的拟合效果较差。

对20年生杉木的3块样地，正态分布、Weibull分布、对数正态分布、Gamma分布对其拟合效果达到显著水平的样地数分别为1块、0块、0块和0块，总体来看，4种函数对20年生杉木直径结构的拟合效果均不理想。

由图1进一步直观看出，6年生杉木3块样地，用对数正态分布拟合的曲线与实际株数组成的曲线接近程度都最高，拟合效果最好，Gamma分布拟合的效果次之，正态分布拟合的接近程度都不理想，Gamma分布和对数正态分布对样地3的拟合与实际最接近。13年生杉木3块样地，Weibull分布的拟合曲线与实际分别曲线最接近，拟合效果最好，对数正态分布拟合的接近程度都不理想。Weibull分布对样地4的拟合与实际最接近。20年生杉木3块样地，4种分布函数的拟合曲线与实际分布情况都有较大差别，拟合效果普遍不理想。通过作图比较拟合曲线与实际株数曲线的接近程度可知，各分布函数的拟合效果与表4的检验结果相吻合。

4 结论与讨论

（1）福寿林场杉木林分的平均直径、直径分布范围及直径标准差随着林龄的增大而增大。从偏度系数看，偏度系数都为正值，直径分布曲线为左偏，胸径均值位于大于峰值的一边，右边有一条长尾，分布偏向中小径阶，偏离程度上，6年生杉木偏离程度最大，呈现反J型变化的趋势，20年生次之，13年生偏离程度最小，这是因为6年生杉木林分还未完全分化，直径变化差距不大，13年、20年杉木已经分化，直径变化差距相对较大，同时由于6年生杉木林分直径普遍较小，用1 cm作为径阶对幼龄林来讲偏大，这方面尚需进一步研究。从峰度系数看，6年生都为正值，直径分布比较集中，分布曲线比正态分布陡峭，呈尖峰态，其中样地2峰度系数最大，分布曲线最陡峭，13年、20年的杉木除样地8外都为负值，直径分布总体比较离散，比正态分布平缓，呈低峰态，这是因为一方面，最初林木大小相差不大，分布较集中，之后随着林龄的变化，由于林木本身特性及所处微环境的不同，不同林木之间产生了分化，直径分布相对变的较为离散，同时，在林分生长过程中，进行了人为的抚育经营管理，受到一定程度的人为活动干扰，间伐林木的不同对林分直径的分布有较大影响，在调整过大的林分密度样地后，林分直径的分布也会发生变化，另外，直径的分布情况与采集的样本质量也有关系。

（2）对杉木人工林直径分布的拟合，6年生杉木，对数正态分布和Gamma分布两种分布函数的拟合效果较好，Weibull分布的拟合效果一般，正态分布的拟合效果不理想。13年生杉木，Weibull分布的拟合效果好，Gamma分布和正态分布的拟合效果一般，对数正态分布的拟合效果不理想。20年生杉木，4种分布函数的拟合效果均不理想。可见，林分不同直径分布规律一般也不同，在研究直径分布规律时要根据不同的林分类型选择不同的分布函数。13年生杉木直径分布相对较接近正态分布，直径结构分布较理想，6、20年生杉木直径结构与正态分布有较大差距，分布不够理想，这与林场的人为干扰，不合理经营有关，间伐时没有充分考虑林木的直径大小，因此，为了更好地提高福寿林场的生产力，充分发挥其经济、生态效益，利于森林的永续利用，需要调整林分内部直径株数分布。如可通过抚育，团状采伐，人工补植，对于密度过大的可采用疏伐使幼树生长等一些措施，最终使直径结构逐步趋于合理，生态效能更好发挥。

[1] 李 俊,佘济云,胡焕香,等.昌化江流域天然林直径结构研究[J].中南林业科技大学报,2012,32(3):37-43.

[2] 孟宪宇.测树学[M].北京:中国林业出版社,2008:73-86.

[3] 左 政,许彦红,朱 霖,等.香格里拉高山松林分直径结构分析[J].西南林业大学学报,2011,31(2):29-32.

[4] 黄家荣,高光芹,孟宪宇,等.基于人工神经网络的林分直径分布预测[J].北京林业大学学报,2010,32(3):21-27.

[5] 胡焕香,佘济云,刘立武,等.海南阿陀岭4种加勒比松林分直径分布规律研究[J].中国农学通报,2012,28(22):16-21.

[6] 张建国,段爱国,童书振.林分直径结构模拟与预测研究概述[J].林业科学研究,2004,17(6): 787-795.

[7] 姚爱静,清 科,张宇清,等.林分结构研究现状与展望[J].林业调查规划,2005,30(2):70-76.

[8] 姜 磊,陆元昌,廖声熙,等.滇中高原云南松林分直径结构研究[J].林业科学研究,2008,21(1):126-130.

[9] 惠淑荣,吕永震. Weibull分布函数在林分直径结构预测模型中的应用研究[J].北华大学学报:自然科学版,2003,4(2):101-104.

[10] 周春国,佘光辉,吴富桢,等.用变形Weibull分布对热带雨林结构规律的研究[J].南京林业大学学报,1998,22(4):12-16.

[11] 张 文,高天雷.马尾松林分直径结构研究[J].四川林勘设计,2001,(2):26-30.

[12] 邓坤枚,邵 彬,李 飞.长白山北坡云冷杉林胸径、树高结构及其生长规律的分析[J].资源科学, 1999,21(1):77-84.

[13] 盛 棸,谢千式,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2000,22(1):157-439.

[14] 马 琳,梁 军,周国英,等.昆嵛山天然赤松次生林空间结构特征的研究[J].中南林业科技大学学报,2013,33(9):50-54.

Study of diameter distribution of Cunninghamia lanceolata artif i cial forests with different stand age in Fushou forest farm

ZHOU Yong-qi, LI Ji-ping, CAO Xiao-yu
(School of Forestry, Central South University of Forestry & Technology, Changsha 410004, Hunan, China)

By taking Cunninghamia lanceolata artif i cial forests in Fushou forest farm as the tested objects, the diameter distributions of C. lanceolata artif i cial forests from 9 sampling plots with three stand age were investigated and fi tted based on 4 distribution functions(normal distribution, Weibull distribution, lognormal distribution, Gamma distribution). The results indicate that the coefficients of skewness were positive values, in other words, the numbers of medium and small diameter class were more than that of the large, the coeff i cient of skewness of 6-year-old C. lanceolata was the largest and the coeff i cient of skewness of 13-year-old was the smallest;The coefficients of kurtosis of 6-year-old C. lanceolata were positive values, the diameter distribution was more concentrated, the coeff i cients of kurtosis of most of the 13-year-old and 20-year-old were negative values, the diameter distribution was decentralized; The fi tting effects of 6-year-old C. lanceolata fi tted with lognormal distribution and Gamma distribution methods were very good, that of 13-year-old C. lanceolata fi tted with Weibull distribution also were, while that of 20-year-old C. lanceolata fi tted were not satisfactory.

Cunninghamia lanceolata plantation; diameter distribution; distribution functions; forest stand age

S791.27

A

1673-923X(2014)07-0061-06

2014-03-10

国家“十二五”科技支撑计划项目（2012BAD22B0505）；湖南省教育厅项目（12C0440）

周永奇（1985-），男，河南上蔡人，硕士研究生，主要研究方向：林业系统工程、生物质能源

李际平（1957-），男，湖南醴陵人，教授，博士，博士生导师，主要研究方向：林业系统工程、生物质能源

[本文编校：吴 毅]