基于势平衡的小口径模压可燃药筒装药内弹道计算

邹伟伟，郑启龙，周伟良，田书春，赵振宇

（1.南京理工大学 化工学院，南京210094；2.西安北方惠安化学工业有限公司，西安710302）

可燃药筒作为模块化装药系统中的重要组成元件［1］，是一种含能的结构性多孔材料，具有容器与提供能量的双重作用，目前已在主战坦克及大中口径自行火炮中得到广泛的应用［2］。可燃药筒在火炮发射过程中与主装药共同燃烧，参与内弹道的全过程，对整个装药的内弹道性能具有重要的影响［3］。与符合几何燃烧规律的火药相比，可燃药筒呈现出渗透性燃烧的特点，具有特殊的燃烧规律［4］，无法采用经典内弹道理论描述可燃药筒装药的实际燃烧过程。因此，在弹道计算中如何处理可燃药筒，成为火炮内弹道研究中的一个突出问题。

内弹道势平衡理论是通过对膛内实测压力曲线大量数据的分析，在深入研究膛内热力学过程的基础上提出来的［5］。该理论以实测的压力－时间曲线为基础，用膛内实际气体生成函数代替以几何燃烧定律为基础的气体生成函数，以势平衡点的状态作为标准态，建立内弹道数学模型，运用宏观综合的分析方法，研究膛内复杂的火药燃烧规律与弹道过程［6－8］，为研究装药膛内燃烧规律提供了新的观点和方法，同时也为可燃药筒装药内弹道数值模拟提供了新的思路。

本研究运用内弹道势平衡理论，结合小口径（25mm）可燃药筒定容燃烧的压力－时间曲线与主装药膛内燃烧的压力－时间曲线，研究了弹道炮在可燃药筒装药下的膛内实际燃烧规律，并在此基础上建立了小口径可燃药筒装药的内弹道解法。

1 基本原理

1.1 基本假设

在可燃药筒装药内弹道模拟过程中，药筒的有关参数均用下标1表示，主装药的下标是2。小口径可燃药筒与主装药的质量百分比分别为ω1、ω2，且ω1＋ω2＝1。

小口径可燃药筒及主装药的实际燃气生成函数以相对压力冲量表示（式1），二者组成的混合装药的燃气生成量ψ符合公式（2），且小口径可燃药筒燃烧结束点为K。

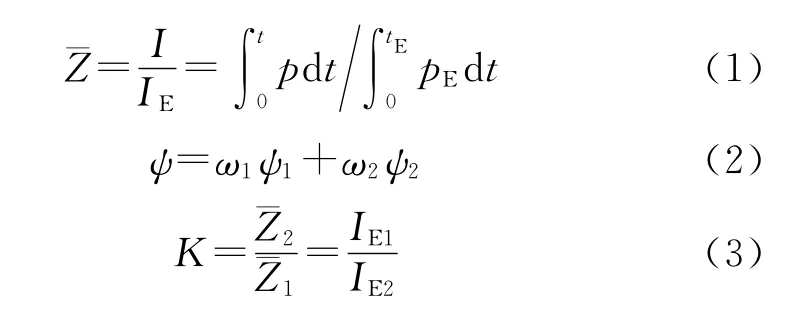
式中：I，p分别为某一瞬间小口径可燃药筒装药的压力冲量和压力；ψ1，ψ2分别为小口径可燃药筒与主装药的相对已燃百分数；ψ为小口径可燃药筒装药的相对已燃百分数；IE1，IE2分别为小口径可燃药筒与主装药的势平衡点对应的压力冲量；IE，tE，pE分别为小口径可燃药筒装药势平衡点对应的压力冲量、时间及压力。

1.2 小口径可燃药筒装药的势平衡点参数

小口径可燃药筒装药的弹道解是以势平衡点为标准态的相对量，因此为得到药筒装药的弹道参量的变化规律，必须求得药筒装药的势平衡点对应的参数，其中药筒装药势平衡点对应的已燃百分数是其它参量求解的基础。

根据火炮实测的主装药的压力-时间曲线，由势平衡点的能量关系式和冲量关系式［7］可求出主装药的势平衡点的燃烧百分数ψE2，其表达式为

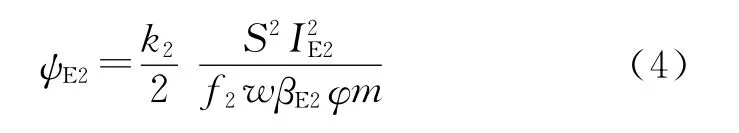
式中：S为炮膛截面积；m为弹丸质量；w为装药量；f2为主装药的火药力；k2为主装药燃气产物的比热比；βE为余容影响系数，均为无量纲量；φ是与平均压力相应的次要功系数。

在可燃药筒装药中，主装药具有较大的质量比，所采用的抽滤模压工艺制备的可燃药筒在达到最大压力前已基本燃完，因此混合装药的势平衡点主要由主装药的统计平均厚度所决定，当主装药燃至ψE2时，药筒装药也相应地达到势平衡点，所以小口径可燃药筒装药的ψE为

由ψE与IE的关系式：

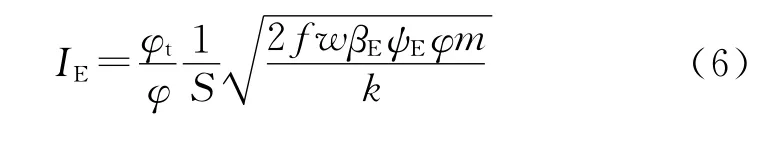
式中：f为装药的火药力，φt是与膛底压力相应的次要功系数，k为整体装药燃气产物的比热比。

由式（6）可得到IE，结合弹丸运动方程可求得此时弹丸速度vE为

由实测的小口径可燃药筒装药的最大压力pm，可求得pE，则：

根据势平衡点的时空关系式（9）可求得势平衡点对应的药室容积VE。

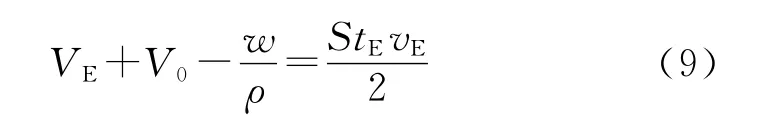
式中：V0为药室容积，ρ为密度。

1.3 实际燃气生成函数的确定

考虑到火炮膛内燃烧情况，小口径可燃药筒在装药达到最大压力前主体部分已基本燃尽，其燃烧环境与定容条件下差别不大，因此将密闭爆发器试验测得的小口径可燃药筒的p1－t曲线用于火炮膛内弹道计算。

采用内弹道基本方程将实测的小口径可燃药筒定容燃烧的p1－t曲线及主装药膛内燃烧的p2－t曲线换算成ψ－t曲线，进而换算成ψ－I曲线。以相对压力冲量¯Z为自变量，将ψ－I曲线转化为曲线，并应用最小二乘法对曲线进行拟合，从而得到小口径可燃药筒与主装药的燃气生成函数，以三项式表示。一般地，主装药采用多孔火药，因此以势平衡点ψE2为边界条件，将主装药的整个燃烧过程分为主体燃烧阶段与碎粒燃烧阶段。

小口径可燃药筒的燃气生成函数：

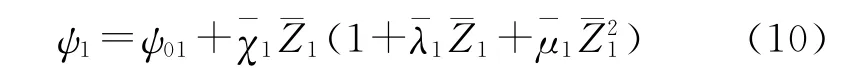
主装药主体燃烧阶段的燃气生成函数：

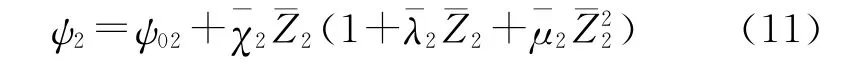
主装药碎粒燃烧阶段的燃气生成函数：

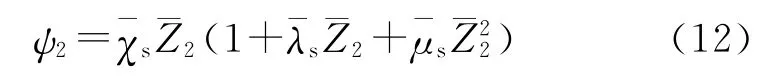
式中：ψ01，ψ02分别为小口径可燃药筒与主装药的表观初始相对已燃百分数；为装药的形状特征量。

应用小口径可燃药筒与主装药的燃气生函数，采用式（2）即可解出小口径可燃药筒装药的燃气生成函数。

一般情况下，在膛内燃烧过程中可燃药筒在达到装药的势平衡点时已经燃完。因此，将小口径可燃药筒装药的整个燃烧过程分为3个阶段，具体如下。

①可燃药筒燃烧结束前阶段。

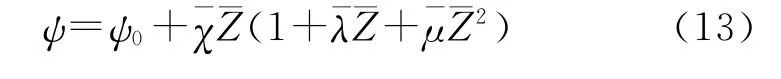
式中：

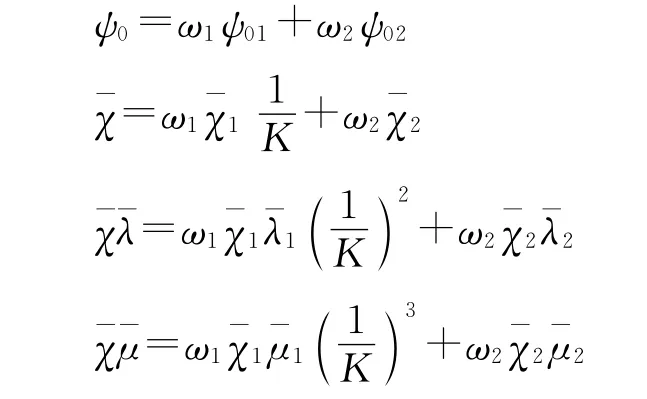
②可燃药筒燃完至势平衡点的阶段。

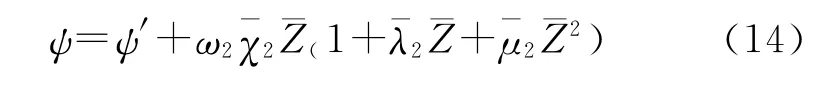
式中：

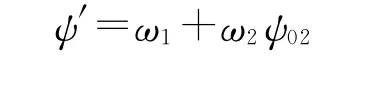
③碎粒燃烧阶段。

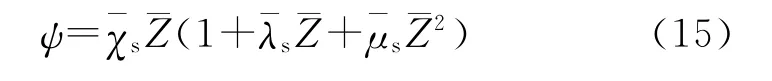
1.4 小口径可燃药筒装药的内弹道模型

以小口径可燃药筒装药各阶段的燃气生成函数为基础，结合引入态能和态能势的内弹道方程和弹丸运动方程［9］，转化得到以势平衡点为标准态的弹道相似方程组：

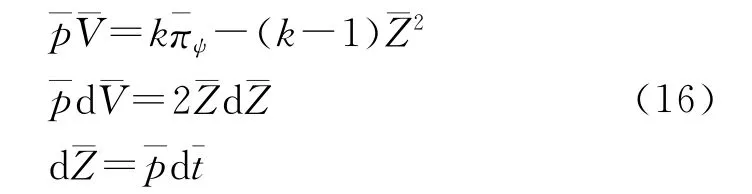
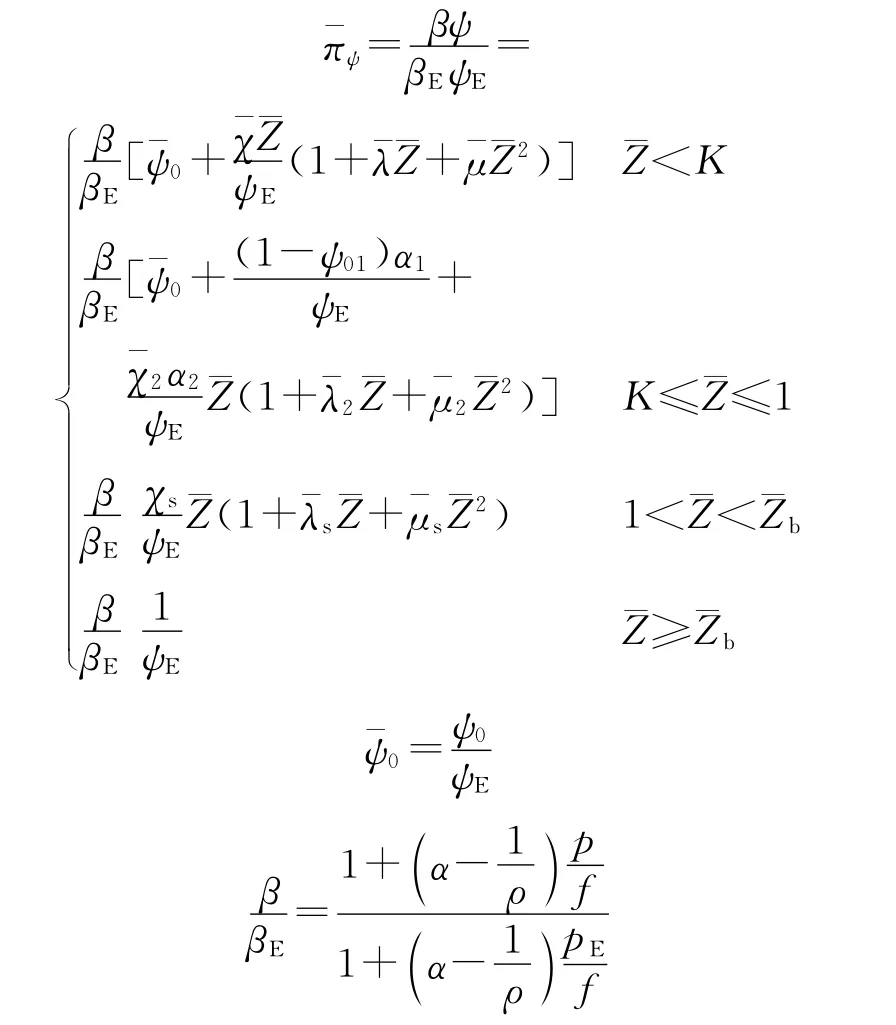
式中：α为余容，下标b表示燃烧结束。

以＝1、＝1＝1为初始条件进行弹道计算，将解出的各弹道相对量分别与势平衡点处的弹道量相乘即得到各瞬间的弹道量，具体计算公式为

2 计算条件

以口径为25mm可燃药筒弹道炮坡膛处测得的主装药的p1－t曲线及定容燃烧试验测得的可燃药筒的p2－t曲线（装填密度为0.12g／cm3）为标准进行计算。

弹道炮结构参数：药室容积V0＝0.4dm3，炮膛截面积S＝0.17dm2，弹丸质量m＝0.23kg，弹丸全行程长为18.2dm。

主装药采用花边十九孔火药，弧厚为0.65～0.80mm，长度为6.5～9.5mm。在金属药筒中的装药量为0.119kg，其真密度ρ2＝1.6kg／dm3，火药力f2＝1 020.5kJ／kg，余容α2＝1.18L／kg。

小口径可燃药筒以硝化棉、硫酸盐木浆纸、粘结剂和助剂为原材料，采用抽滤模压工艺制备，其真密度ρ1＝1.55kg／dm3，火药力f1＝537.9kJ／kg，余容α1＝1.30L／kg。

小口径可燃药筒装药中主装药质量为0.094kg，可燃药筒质量为0.027kg，二者组成的混合装药的火药力f＝994kJ／kg，余容α＝1.05L／kg。

定容燃烧试验采用容积为109mL的密闭爆发器，MANFRAMEJV5300A 采 集 系 统，SYC－3000099120传感器，2号硝化棉为点火药，以点火压力10MPa确定点火药量。

计算过程中所采用的真密度是通过Micromeritics AccuPycⅡ1340型真密度分析仪测试得到的，测试介质为高纯氦气，测试原理为气体置换法，测试温度（25±2）℃，每个试样测试3次求平均值。火药力、余容是按照GJB5472.9－2005标准测试得到的。

3 结果与讨论

3.1 小口径可燃药筒装药燃气生成函数

小口径可燃药筒定容燃烧的p1－t曲线如图1（a）所示（图中曲线为药筒3发平行试验数据），装填密度为0.12g／cm3。从图中曲线可看出，同一个试样3发试验的结果具有较好的重现性。图1（b）为小口径弹道炮采用主装药（金属药筒装药）测得的p2－t曲线，为单次试验测试结果。

采用势平衡理论对小口径可燃药筒与主装药的p－t曲线进行转化、拟合，可得到二者燃气生成函数的拟合系数，具体数值见表1。同时，利用实测的主装药p2－t曲线可得到主装药的势平衡点对应的参数，包括压力冲量IE2＝678.3kPa·s，压力pE2＝215.9MPa，时 间tE2＝3.09ms，速 度vE2＝932.9m／s。应用式（4）可得到主装药的势平衡点的燃烧百分数ψE2＝96%，依据实测的可燃药筒装药的最大压力（见表2），结合式（5）～式（9）可计算得到小口径可燃药筒装药势平衡点对应的参数，其中小口径可燃药筒装药势平衡点对应的已燃百分数ψE＝96.9%，压力冲量IE＝667.1kPa·s，压力pE＝212.8MPa，时间tE＝3.13ms，速度vE＝931.9m／s。

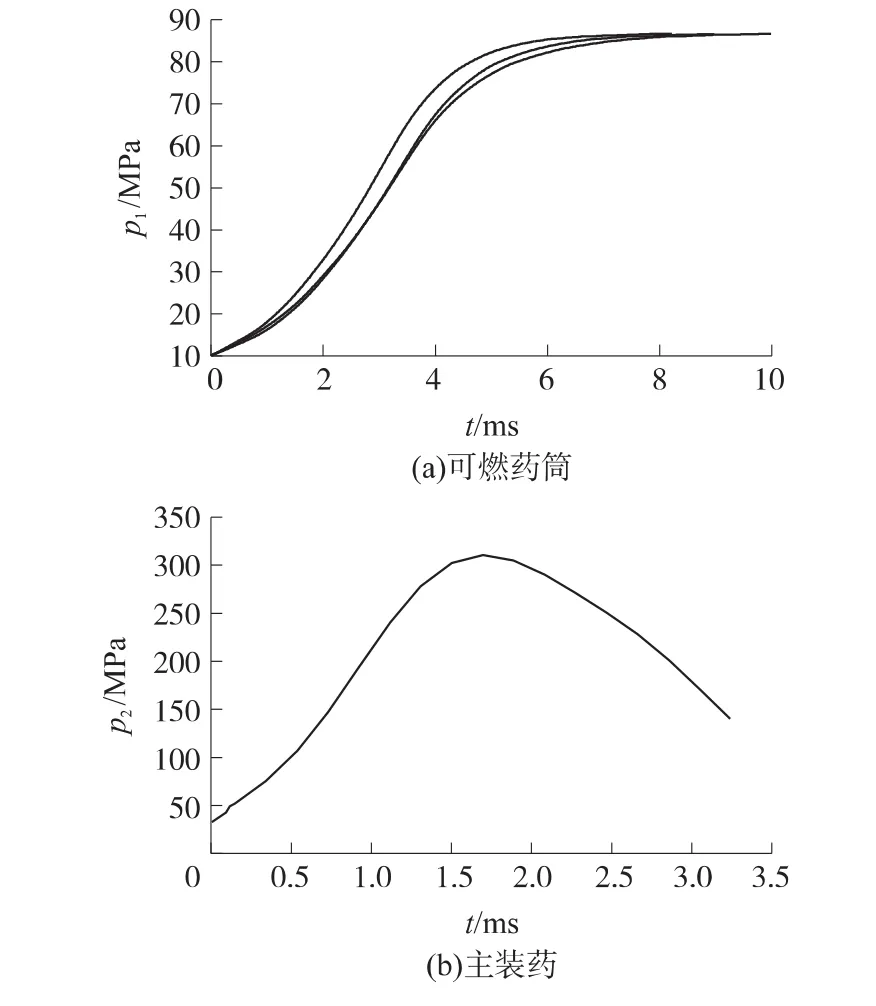
图1 小口径可燃药筒定容燃烧的p1－t曲线与主装药膛内燃烧的p2－t曲线

表1 小口径可燃药筒与主装药燃气生成函数的拟合系数

由表1中数据，可以得到可燃药筒与主装药的燃气生成函数如下。

可燃药筒的燃气生成函数为

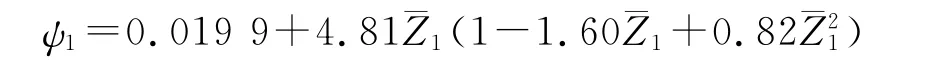
主装药的增面燃烧阶段燃气生成函数为

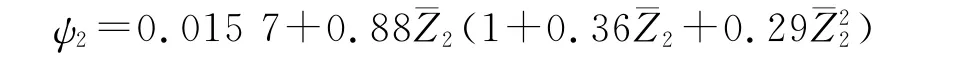
主装药的减面燃烧阶段燃气生成函数为

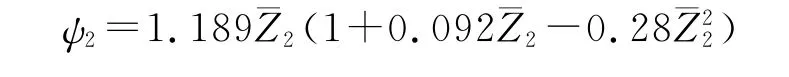
结合可燃药筒与主装药的燃气生成函数，采用式（13）～式（15）可得到小口径可燃药筒装药的燃气生成函数。

可燃药筒燃烧结束前阶段：

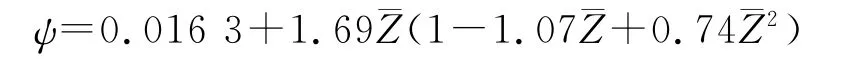
可燃药筒燃完至势平衡点的阶段：

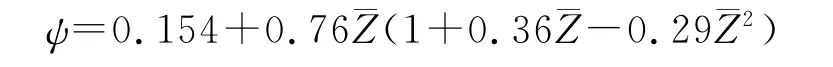
碎粒燃烧阶段：

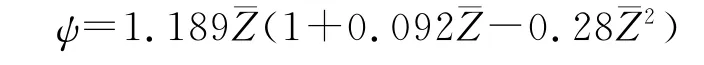
3.2 内弹道模拟

以上述求得的小口径可燃药筒装药膛内实际燃气生成函数为基础，运用内弹道模型对25mm弹道炮的内弹道过程进行了模拟计算，得到了内弹道全过程的压力－时间曲线和特殊点的值。图2为25mm弹道炮在可燃药筒装药下的计算曲线和实测曲线的比较，而特殊点的实测值与计算值如表2所示，包括最大压力pm、达到最大压力的时间tm、初速v0、炮口压力pg及结束时间tg。小口径可燃药筒装药燃烧过程的压力及相应的燃烧时间（实测值）是运用电传感器测压系统测试得到的，而弹丸初速是采用天幕靶测速系统测试得到的。

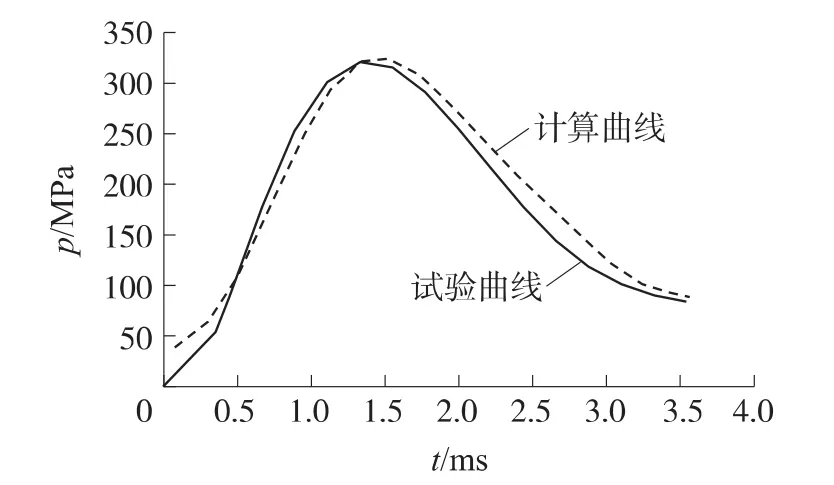
图2 25mm弹道炮在可燃药筒装药下的p－t曲线

表2 特殊点的试验值与计算值

由图2可知，模拟计算得到的p－t曲线与实测曲线能够较好地吻合，计算值与实测值的最大相对误差小于5%。因此，计算曲线可以反映出小口径可燃药筒装药燃烧期间的膛内压力变化规律。

从上述分析中可以看出，内弹道势平衡理论在一定程度上可以模拟小口径可燃药筒装药的内弹道过程。

4 结束语

以实测的小口径可燃药筒定容燃烧的压力－时间曲线与主装药膛内燃烧的压力－时间曲线为标准，应用内弹道势平衡理论确定了小口径可燃药筒装药的燃气生成函数，以三次函数的拟合式表示，其包括3个阶段：可燃药筒燃烧结束前阶段、可燃药筒燃完至势平衡点阶段及碎粒燃烧阶段。

运用内弹道势平衡理论及小口径可燃药筒装药膛内实际燃气生成函数求出的弹道解与试验结果基本一致，可以描述和分析小口径可燃药筒装药膛内实际燃烧规律，拓展了内弹道势平衡理论的应用范围。

［1］XIAO Le－qin，ZOU Wei－wei，LI Yu，et al.Fractal dimension of pore structure of combustible cartridge cases［J］.Journal of China Ordnance，2012，8（2）：109－113.

［2］SHEDGE M T，PATEL C H，TADKOD S K.Polyvinyl acetate resin as a binder effecting mechanical and combustion properties of combustible cartridge case formulations［J］.Defence Science Journal，2008，58（3）：390－397.

［3］乔丽洁，堵平，廖昕，等.可燃药筒对模块装药燃烧残渣的影响［J］.兵工学报，2011，32（10）：1 250－1 254.QIAO Li－jie，DU Ping，LIAO Xin，et al.Influence of combustible case on combustion residue of modular charges［J］.Acta Armamentarii，2011，32（5）：1 250－1 254.（in Chinese）

［4］KURULKAR G R，SYAL R K，SINGH H.Combustible cartridge case formulation and evaluation［J］.Journal of Energetic Materials，1996，14（2）：127－132.

［5］刘林林，马忠亮，萧忠良.变燃速发射药膛内燃烧与内弹道过程研究［J］.兵工学报，2010，31（4）：409－413.LIU Lin－lin，MA Zhong－liang，XIAO Zhong－liang.Research on the actual combustion and interior ballistics process of the variable－burning rate propellant in cannon［J］.Acta Armamentarii，2010，31（4）：409－413.（in Chinese）

［6］肖正刚，应三九，徐复铭.深钝感球扁药混合装药的势平衡理论模拟［J］.弹道学报，2006，18（1）：80－82.XIAO Zheng－gang，YING San－jiu，XU Fu－ming.Potential equilibrium theory simulation of deep－deterred oblate spherical powder mixed propelling charge［J］.Journal of Ballistics，2006，18（1）：80－82.（in Chinese）

［7］鲍廷钰，邱文坚.内弹道学［M］.北京：北京理工大学出版社，1995.BAO Ting－yu，QIU Wen－jian.Interior ballistics［M］.Beijing：Beijing Institute of Technology Press，1995.（in Chinese）

［8］徐文娟，庄国镇.抽滤型可燃药筒加主装药的静态试验研究［J］.弹道学报，1993，5（2）：52－59.XU Wen－juan，ZHUANG Guo－zhen.Static experimental study on cartridge with extracted combustible case［J］.Journal of Ballistics，1993，5（2）：52－59.（in Chinese）

［9］金志明.枪炮内弹道学［M］.北京：北京理工大学出版社，2004.JIN Zhi－ming.Interior ballistics of gun［M］.Beijing：Beijing Institute of Technology Press，2004.（in Chinese）