弹道导弹弹道面转移变换规划方法
2014-12-26王继平王安民魏诗卉张宪伟
王继平,王安民,魏诗卉,张宪伟
(1.第二炮兵装备研究院,北京100085;2.中国人民解放军96271部队,河南 洛阳471000)
传统的弹道导弹飞行过程分为助推段、中段和再入段,助推段动力系统各子级连续工作,即使有间隔,也只是间隔几s时间,中段和再入段合称被动段,被动段在地球引力作用下沿抛物线轨迹惯性飞行,占整个飞行弹道的90%左右,整个飞行弹道近似在发射点、目标点、地心构成的弹道面内[1]。可见,传统弹道导弹存在以下缺陷:①中段惯性飞行时间长、弹道高,易被导弹防御系统探测、跟踪和拦截。以传统弹道为基础的中段变轨机动能力有限,只能实现有限范围内的机动,突防能力有限;②传统弹道导弹一般通过改变飞行程序角来调整发动机能量分配,从而控制弹道高低,实现射程远近的调节。因而,在总体结构和弹头特性一定的情况下,存在最大射程与最小射程的限制。
为此,基于卫星轨道面转移思想[2],提出了一种弹道导弹弹道面转移的策略,通过弹道转移变换规划可获得合适的再入速度、再入倾角和中段惯性飞行时间,实现最大射程范围内的任意射程控制,可有效克服上述缺陷。
传统弹道导弹的飞行通常在一个弹道面内进行制导控制,由于导弹发动机能量是固定的,能够提供的速度大致确定,即关机点速度大小确定,通常先通过射程和关机点速度,根据椭圆弹道理论确定关机点弹道倾角,然后以关机点弹道倾角为约束设计助推段的飞行程序,从而调整发动机能量分配[1,3]。而对于弹道面转移飞行导弹,除各弹道面内通过飞行程序设计分配能量外,还要同时设计弹道面转移变换来分配能量。此时导弹各级发动机能量的分配除了要确定各弹道面内关机点弹道倾角外,还需确定各弹道面导弹的射程角和弹道面变换夹角,采用传统的方法无法实现。由于弹道面转移飞行导弹转移飞行在大气层外,与助推-滑翔导弹相比,不需考虑大气的气动影响和热烧蚀,因而助推-滑翔导弹的弹道优化方法也不适应弹道面转移变换的规划与设计[4]。本文基于椭圆弹道理论[1],采用优化方法对弹道面转移变换进行规划,确定各弹道面弹道参数和弹道面变换夹角,为Ⅱ级、Ⅲ级助推段飞行程序即转移飞行程序设计[2]提供基准,简化了整条弹道优化。
1 弹道面转移变换规划思想
以三级固体发动机导弹为例,如图1所示,是导弹两次变弹道面飞行的一条弹道,各级发动机非连续点火,具有3个助推段和3个转级飞行段,Ⅱ级、Ⅲ级发动机在大气层外为导弹变弹道面飞行提供动力。图中,ΔA为初始弹道面与传统弹道面的夹角,Λ为弹道面变换夹角。
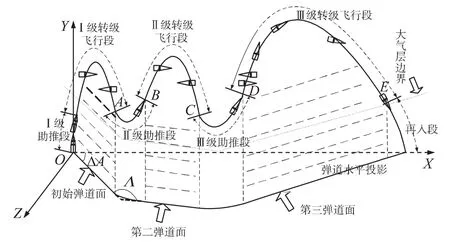
图1 三级发动机导弹飞行弹道面转移示意图
如图2所示,设各级发动机动力能提供的速度分别为v1、v2、v3。它们由下式近似确定:
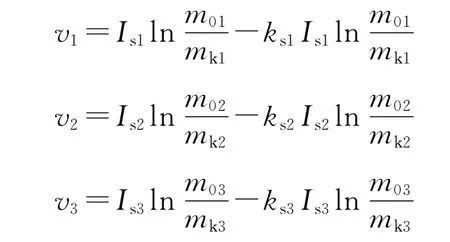
式中:Is1、Is2、Is3分别为第Ⅰ、Ⅱ、Ⅲ级真空比冲;m01、m02、m03分别为第Ⅰ、Ⅱ、Ⅲ级点火质量;mk1、mk2、mk3分别为第Ⅰ、Ⅱ、Ⅲ级熄火质量;ks1、ks2、ks3分别为第Ⅰ、Ⅱ、Ⅲ级速度损耗系数经验值。ks1为考虑Ⅰ级飞行出大气层前气动力和引力造成的速度损失,ks2是考虑Ⅱ级助推段引力假定为恒值造成的速度损失,ks3是考虑Ⅲ级助推段引力假定为恒值造成的速度损失,ks1相比ks2、ks3较大。
为了方便各弹道面发动机能量的规划,假设Ⅱ级和Ⅲ级助推段提供的速度大小瞬间完成,即有下式成立:
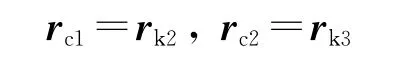
式中:rc1为第一弹道面弹道终点地心矢;rk2为第二弹道面弹道关机点地心矢;rc2为第二弹道面弹道终点地心矢;rk3为第三弹道面弹道关机点地心矢。

图2 弹道面变换夹角和各弹道面弹道参数示意图
假设第一弹道面与第二弹道面夹角为Λ2,第二弹道面与第三弹道面夹角为Λ3。第一弹道面弹道Ⅰ级助推出大气层时的速度大小为vk1,倾角为Θk1,地心距为rk1,椭圆弹道面起始点K1处与正北方向夹角为ΛA,射程角为βc1;第二弹道面弹道关机点速度大小为vk2,倾角为Θk2,地心距为rk2,椭圆弹道面起始点K2处与正北方向夹角为ΛB,由Λ2确定,射程角为βc2;第三弹道面弹道关机点速度大小为vk3,倾角为Θk3,地心距为rk3,椭圆弹道面起始点K3处与正北方向夹角为ΛC,可由Λ3确定,射程角为βc3。
若已知Θk1、ΛA、βc1、Θk2、Λ2、βc2、Θk3、Λ3、βc3,可采用椭圆弹道理论计算各弹道面弹道参数。在给定发射点与目标点的情况下,只要确定参数Θk1、ΛA、βc1、Θk2、Λ2、βc2、Θk3,Λ3、βc3,使其满足各级发动机能量运用要求,就可以设计出一条变弹道面飞行弹道。但上述参数均是未知量,受各级发动机能量和突防要求、射程等约束,求解这些参数的问题是一个优化问题,采用优化方法对其进行确定。
2 弹道面转移变换规划模型
2.1 第一弹道面弹道参数计算
1)由发射点求K1点参数。
先计算弹道倾角为Θk1时,大层外飞行最大射程角βc1max。椭圆弹道能量参数为[1]
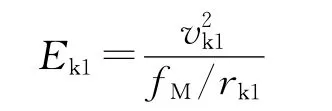
式中:fM为地球引力常数;vk1=v1。
椭圆弹道偏心率为

椭圆长半轴为
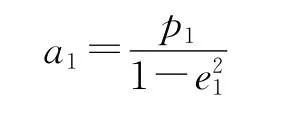
半通径为
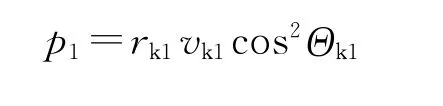
则:
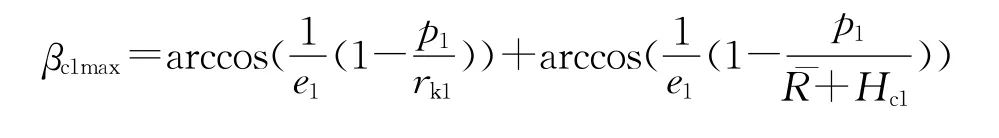
式中:¯R为地球平均半径;Hc1为第一弹道面弹道终点高程,为保证Ⅱ级助推段飞行在大气层外,Hc1取为120km;rk1取为80km。
然后,估算由发射点到K1点的射程角[1]:
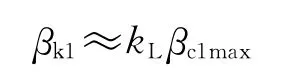
式中:kL为射程比例系数,kL=0.1~0.28,根据弹道高低选取适应的值。
从而,由下式可计算出K1点的经、纬度和方位角:
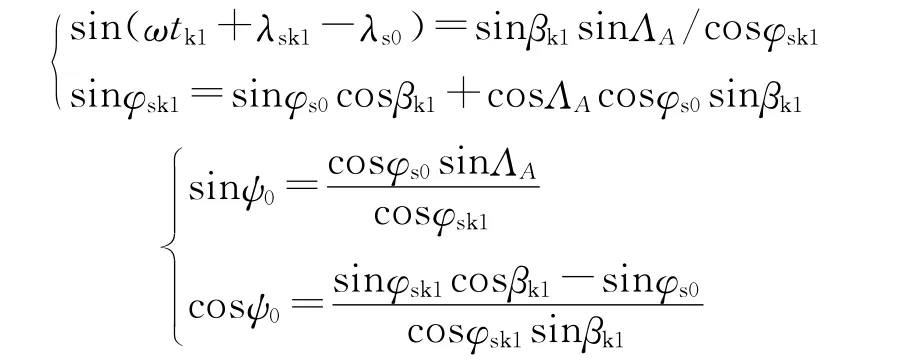
式中:ω为地球自转角速度,tk1为K1点导弹飞行时间,λsk1、φsk1为K1点经、纬度,λs0、φs0为经、纬度,ψ0为K1点弹道面与正北方向夹角,即方位角。
2)弹道终点参数计算。
①首先,由导弹自由段射程角βc1求弹道终点地心矢径rc1。
当Θk1≥0时,有:
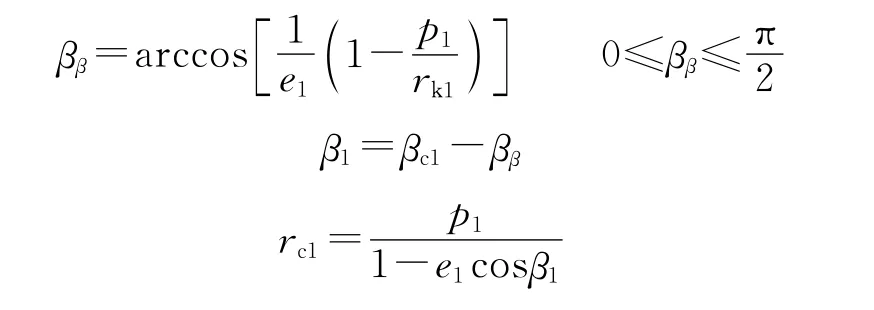
当Θk1<0时,有:
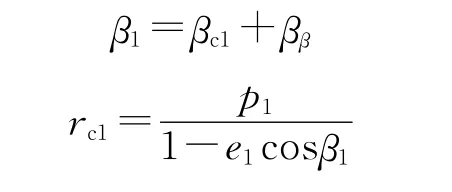
②求弹道终点速度vc1。
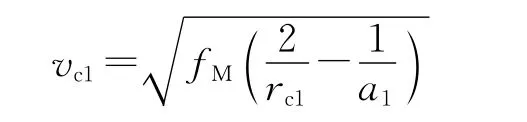
③求弹道终点倾角Θc1。
当Θk1≥0时,有:
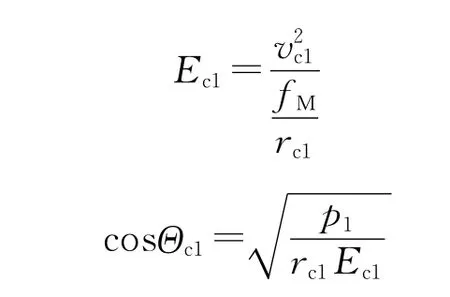
当βc1≥ββ时,Θc1≤0;当βc1<ββ时,Θc1>0。
当Θk<0时,有:

④求自由段飞行时间tc1。
当Θk1≥0时,
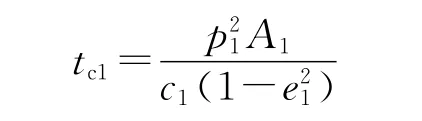
式中:
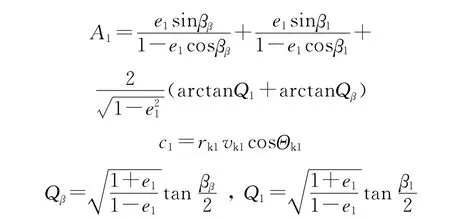
当ββ≥βc时,令β1=-β1,进行计算。
当Θk<0时,令ββ=-ββ,进行计算。
⑤弹道终点经纬度λsc1、φsc1计算。
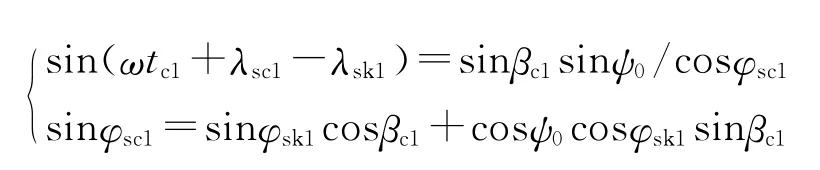
⑥弹道终点处与正北方向夹角ψ1。
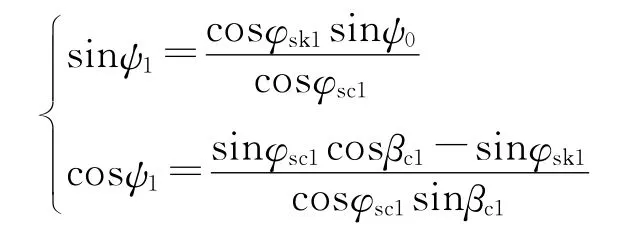
2.2 第二弹道面弹道参数计算
Ⅱ级助推段是恒定推力的持续作用,为了方便各弹道面发动机能量的规划,假设Ⅱ级助推段提供的速度大小瞬间完成,即第一弹道面弹道终点地心距rc1与第二弹道面关机点地心距rk2相等,那么,重力持续作用方向可假定为朝第一弹道面弹道终点地心方向,设Ⅱ级助推段重力造成的速度损失为δvgc1,δvgc1=gc1tg2,tg2为二级发动机工作时间。以此假设为前提对第二弹道面弹道参数进行计算。
1)第二弹道面关机点K2处方位角ΛB计算。
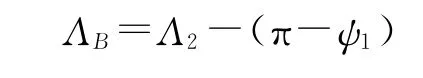
2)关机点速度计算。
第一弹道面弹道终点速度和位置在惯性地心大地直角坐标系Osxsyszs下的分量由下式计算:
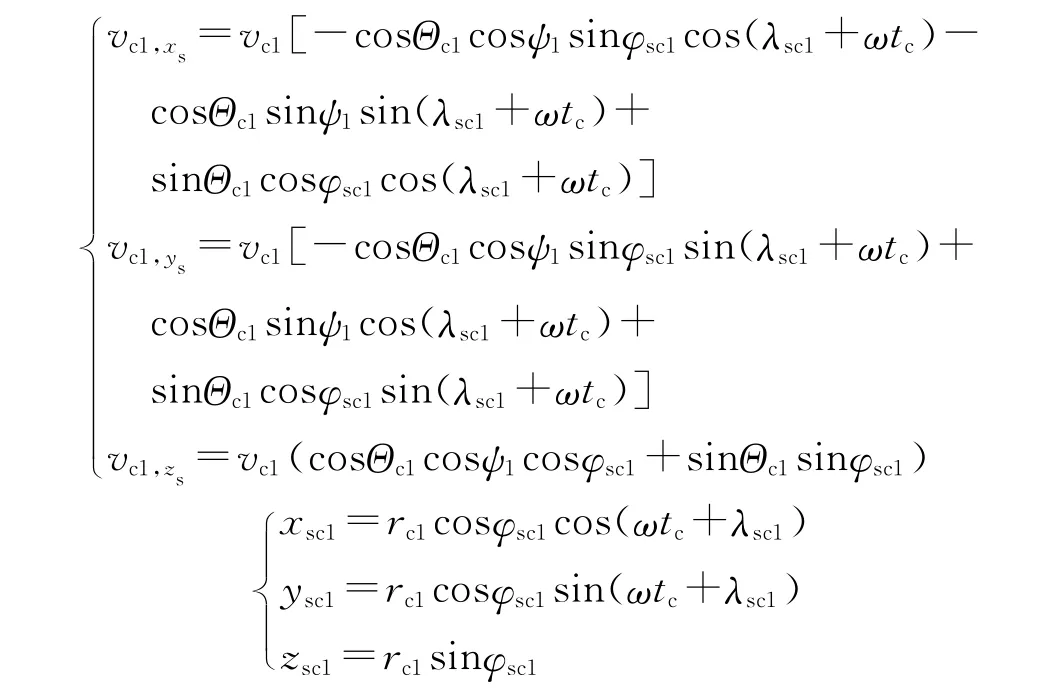
式中:tc=tk1+tc1。
δvgc1在惯性地心大地直角坐标系下的分量由下式计算:
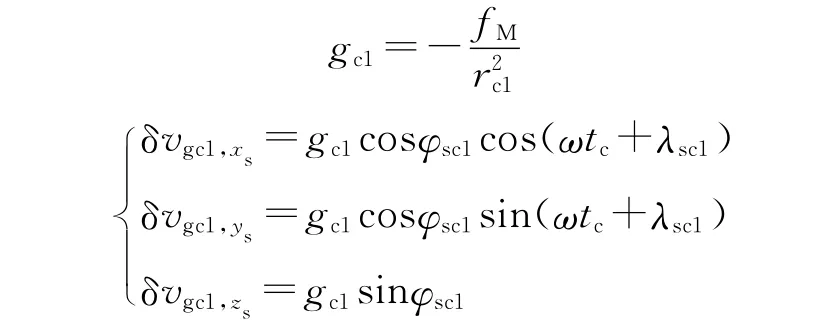
式中:tc=tk1+tc1。
设第二弹道面弹道关机点速度在惯性地心大地直 角 坐 标 系Osxsyszs下 的 分 量 为vk2,xs、vk2,ys、vk2,zs,则有如下关系式成立:
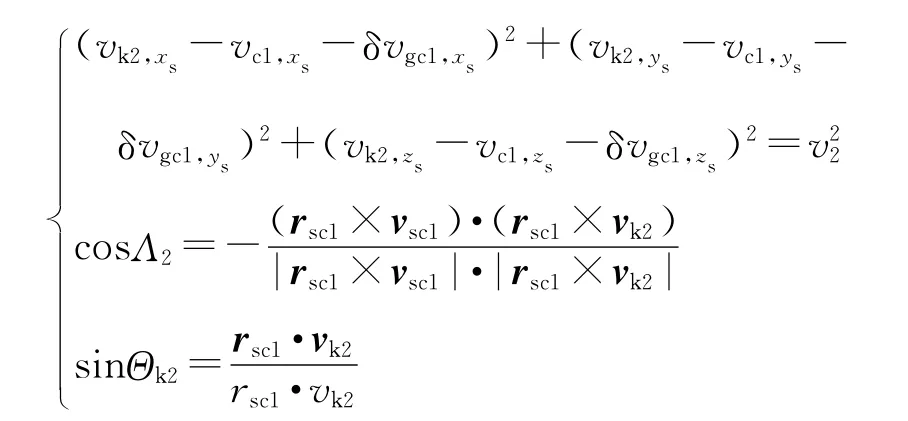
令:
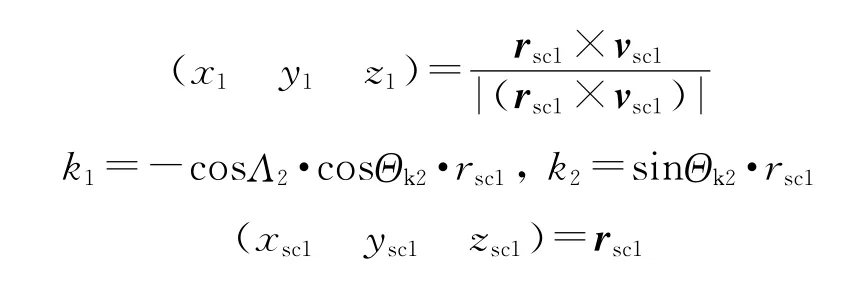
则:
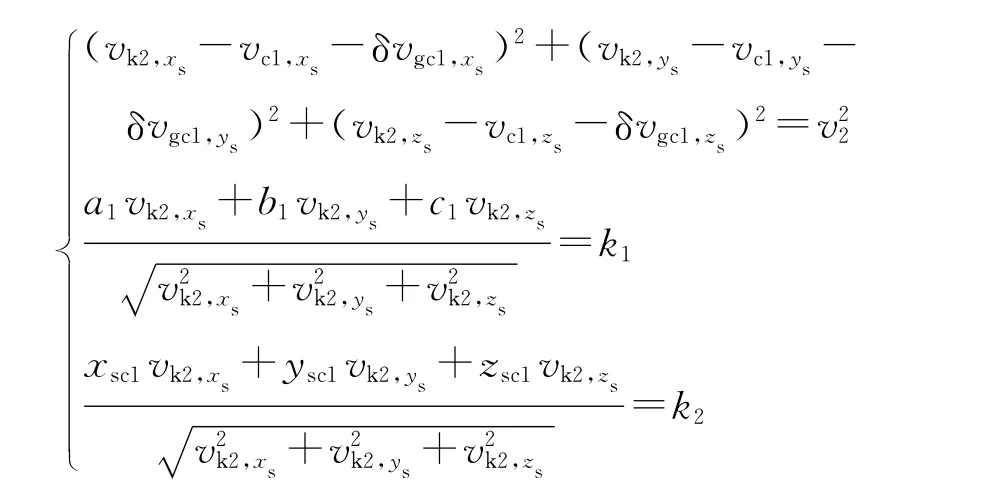
式中:
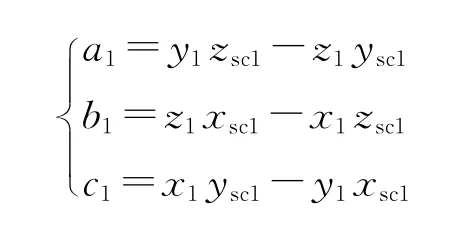
令:
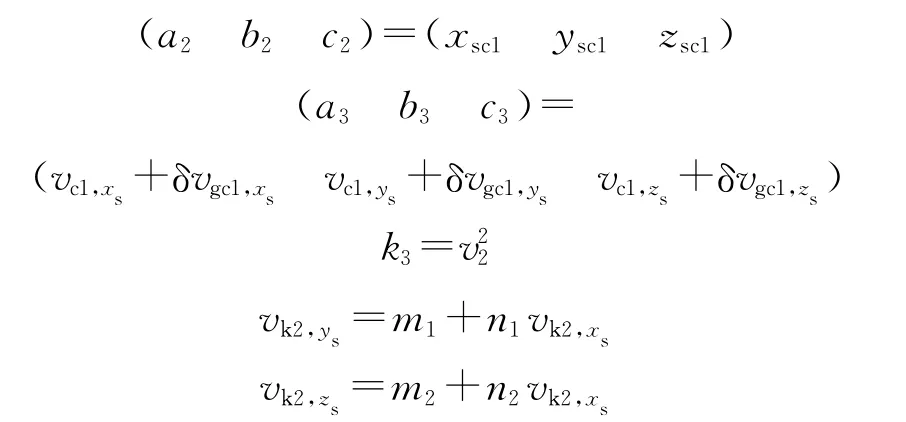
通过Matlab符号方程求解可得:
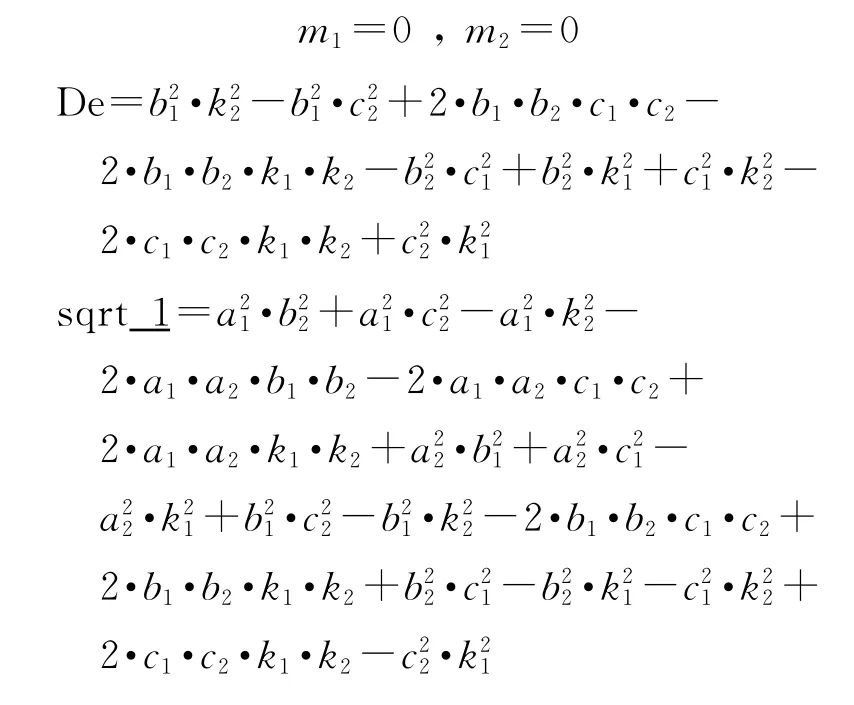
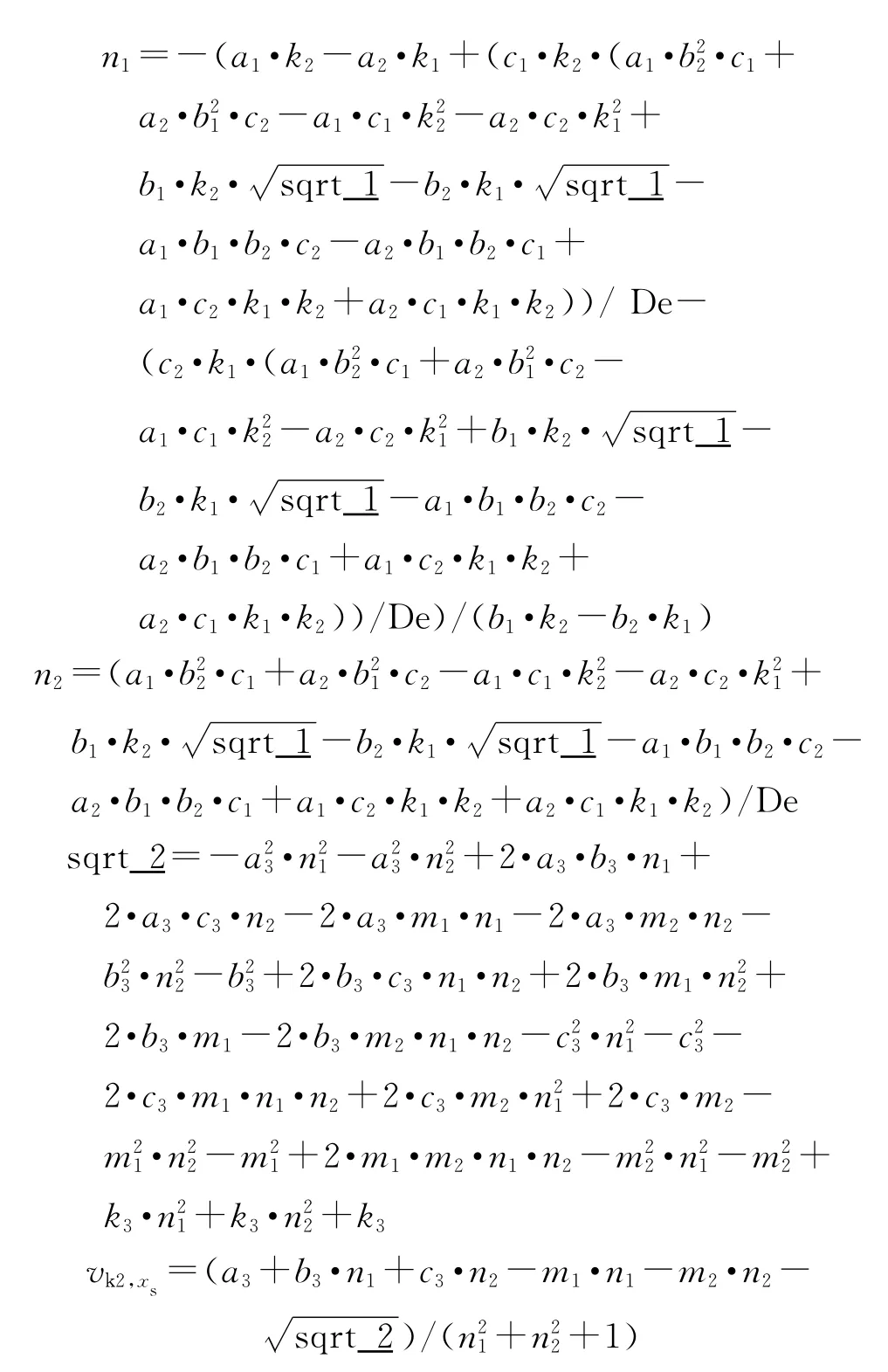
3)弹道终点参数计算。
弹道终点参数计算同2.1节。
2.3 优化目标函数计算
假设v1、v2耗完,要打到目标,第三弹道面弹道采用闭路迭代求关机点需要速度,再与第二弹道面弹道终点参数配合计算Ⅲ级发动机应提供的速度v3p。
关机点需要速度迭代计算方法如下[5]:
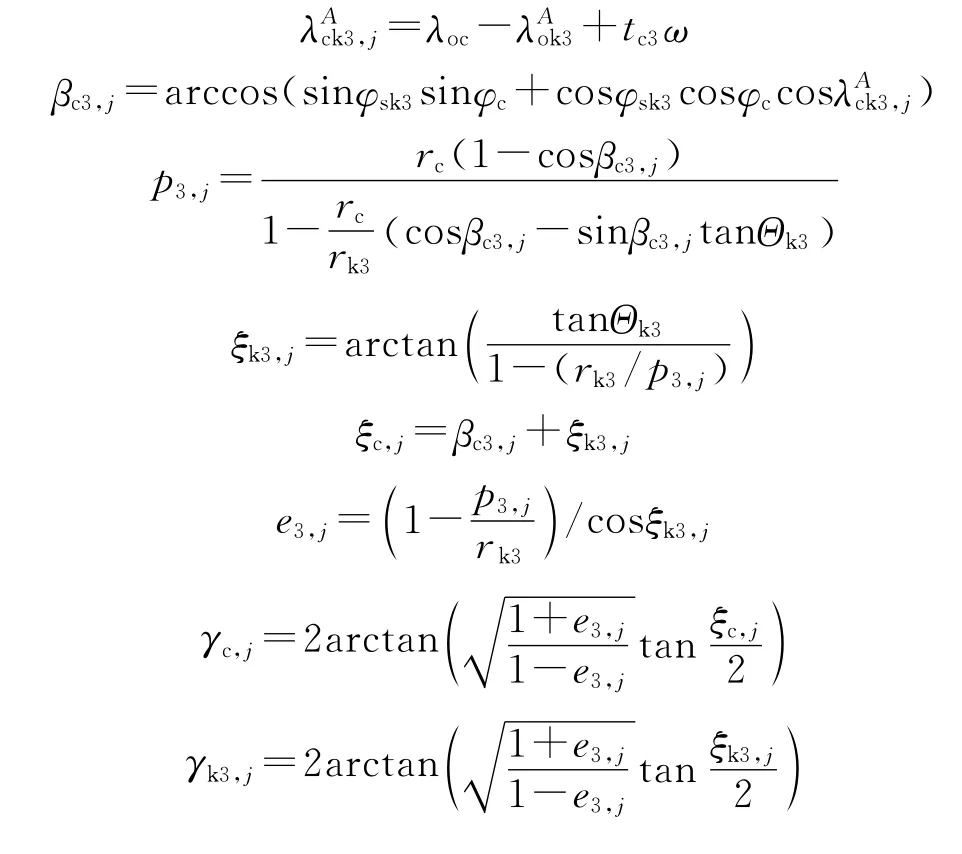
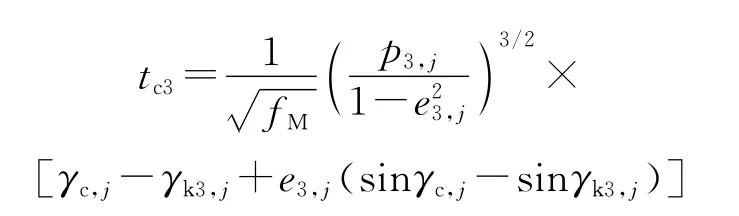
式中:j为迭代次数;下标k3代表第三弹道面关机点;下标c代表第三弹道面椭圆弹道落点,见图2;为导弹关机点K3与第三弹道面弹道落点的绝对经度差;为发射点与关机点K3的绝对经度差;λoc为发射点与第三弹道面椭圆弹道落点的经度差;tc3为第三弹道面椭圆弹道飞行时间;φsk3为导弹关机点K3地心纬度;φc为第三弹道面椭圆弹道落点地心纬度;βc3,j为第三弹道面椭圆弹道射程角;Θk3为关机点K3处弹道倾角;rk3为关机点K3处地心距;rc为第三弹道面椭圆弹道落点地心距;p3,j为第三弹道面椭圆弹道半通径;e3,j为第三弹道面椭圆弹道偏心率。
给定tc3初值进行需要速度迭代,当|p3,j+1-p3,j|<ε=1.0时,结束迭代,可求得需要速度大小vR:
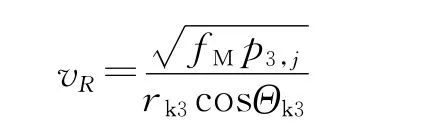
第三弹道面关机点K3处与正北方向夹角为
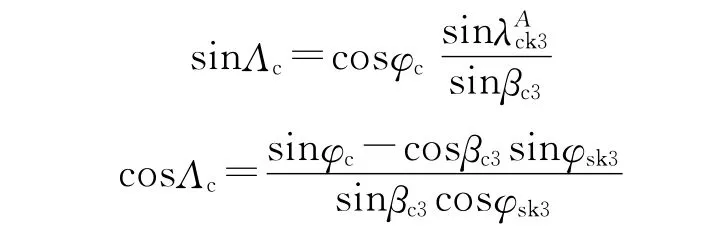
需要速度在惯性直角坐标系下的分量为
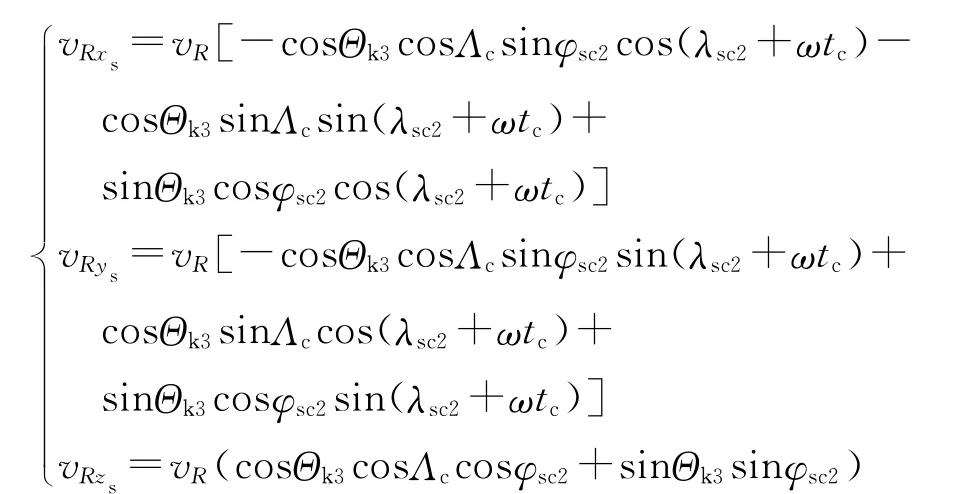
式中:tc=tk1+tc1+tc2。
第二弹道面弹道终点速度在惯性直角坐标系下的分量为
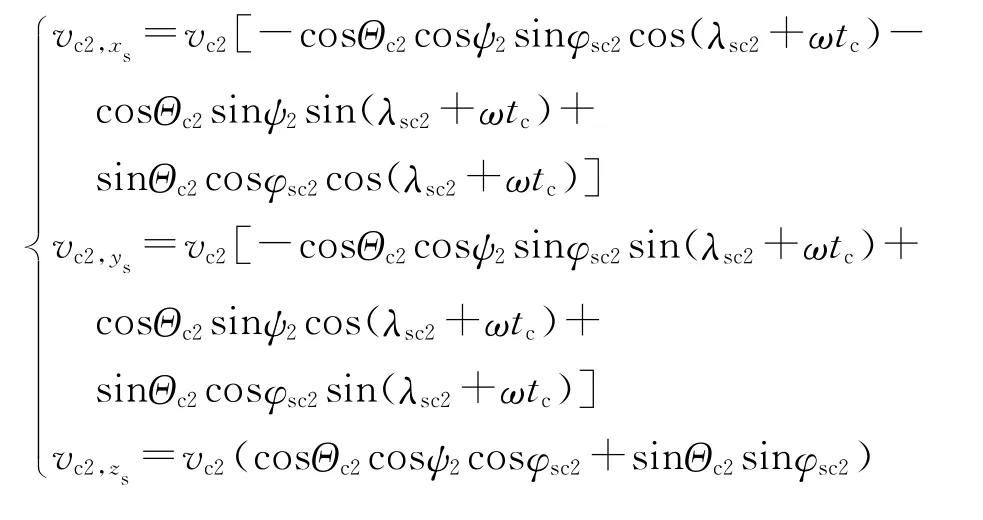
设Ⅲ级助推段重力造成的速度损失为δvgc2,在惯性地心大地直角坐标系下的分量为δvgc2,xs、δvgc2,ys、δvgc2,zs,δvgc2=gc2tg3,tg3为三级发动 机 工 作时间。
需要速度增量为
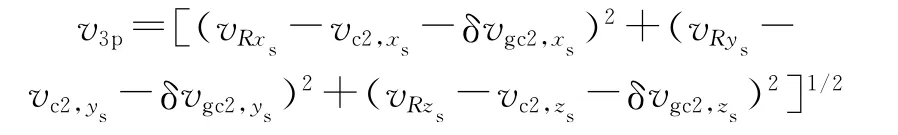
以Δv=v3p-v3最小为优化目标,当|Δv|<ε且Δv<0时,停止搜索,ε是一小量正数。Δv<0表明能量满足要求,导弹能打到目标;|Δv|<ε表示导弹发动机能量充分应用。
3 弹道面转移变换优化
弹道面转移变换的优化问题是:给定发射点与目标点,在搜索空间约束下,以发动机能量充分应用为优化目标,优选的参数有7个:Θk1、ΛA、βc1、Θk2、Λ2、βc2、Θk3。其中给定Θk1、ΛA、βc1、Θk2、Λ2、βc2,根据2.2节方法能求得第二弹道面弹道终点参数,Θk3为第三弹道面弹道关机点需要速度迭代提供倾角,βc3可由2.3节的需要速度迭代确定,Λ3由需要速度方向确定,Λ3=Λc+(π-ψ2),ψ2为第二弹道面弹道终点处与正北方向的夹角,根据需要速度方向算出。
弹道面转移变换优化方法可以采用各种优化计算方法,本文采用随机方向法[6],经验证也能达到很好的搜索效果。搜索空间根据突防、制导等要求确定。
4 仿真算例
4.1 仿真条件
给定发射点经度105°,纬度30°;目标点经度210°,纬度30°,射程约9 600km。假设导弹有四级发动机,一、二级发动机考虑空气动力和重力损失后能提供的总速度大小为5 800m/s,三级发动机能提供的速度大小为3 900m/s,工作时间约为60s,四级发动机能提供的速度大小为3 000m/s,工作时间约为60s。实施两次弹道面转移变换,一、二级发动机连续点火工作,为初始弹道面飞行提供动力;第一次弹道面转移由三级发动机提供动力;第二次弹道面转移由四级发动机提供动力。
搜索空间假设:ΛA搜索范围为70°~90°,Λ2搜索范围为160°~180°,Θk1搜索范围为20°~30°,Θk2搜索范围为0°~40°,Θk3搜索范围为20°~40°;βc1和βc2的搜索范围选取:首先根据Θk1和Θk2确定自由段(大气层外)飞行最大射程βc1max和βc2max,设βc1=l1βc1max,βc2=l2βc2max,l1范围选取为0.8~0.99,l2范围选取为0.5~0.99。
随机方向法调优矢量参数A初值选为0.2,当A<1×10-8时,若满足-5<Δv<0,停止计算,否则A选为0.2,重新选择初值计算。
4.2 仿真结果
通过随机方向法进行优化计算,得到弹道面转移变换规划结果如表1所示。
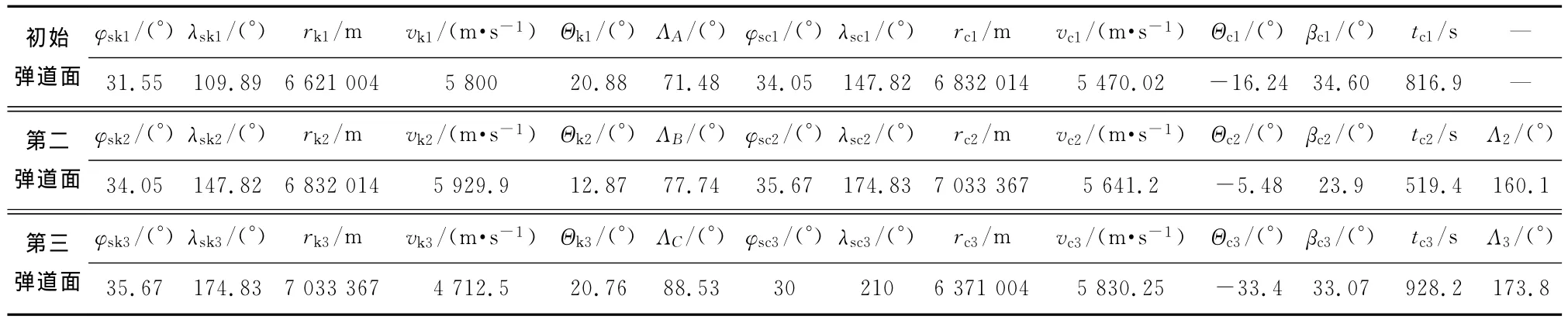
表1 两次弹道面转移变换规划结果
从上表可以看出,在给定的搜索空间内,采用弹道面转移规划模型可以规划各弹道面参数,验证了模型的正确性。采用随机方向法优化计算,经统计搜索次数为1 532次,搜索时间约790ms,可见规划模型的计算量不大,验证了随机方向法的有效性。
传统弹道发射点方位角约56°,最佳弹道倾角约23°,惯性飞行时间约1 904s,比弹道面转移变换弹道每段惯性飞行时间长得多,易被预测和拦截,不利于突防。
5 结束语
弹道导弹弹道面转移变换,可以是一级发动机提供动力,也可以是多级发动机连续工作提供动力,可以进行一次或多次弹道面转移,规划前提是要确定搜索空间,搜索空间根据需求如突防要求等确定。文中假设的搜索空间只为验证规划方法的正确性,没有通过需求给出。另外,在搜索前首先要确定导弹发动机的能量是否充足,否则搜索不出结果,传统弹道是最省能量弹道,按传统弹道的耗能来确定是否有多余的能量用于弹道面转移变换,后续在此方面加强研究,同时进一步进行转移飞行程序的设计研究。
[1]张毅,肖龙旭,王顺宏.弹道导弹弹道学[M].长沙:国防科技大学出版社,2005:173-305.ZHANG Yi,XIAO Long-xu,WANG Shun-hong,Ballistics of ballistic missile[M].Changsha:National University of Defense Technology Press,2005:173-305.(in Chinese)
[2]张万里.轨道转移飞行器的轨迹优化与制导算法研究[D].哈尔滨:哈尔滨工业大学,2011.ZHANG Wan-li.Research on trajectory optimization and guidance algorithm of orbital transfer vehicle[D].Harbin:Harbin Institute of Technology,2011.(in Chinese)
[3]魏鹏涛,王明海.模式搜索法在导弹飞行程序优化设计中的应用[J].弹箭与制导学报,2009,29(1):15-17.WEI Peng-tao,WANG Ming-hai.Application of mode search in flight program optimum design for missile[J].Journal of Projectiles,Rockets,Missiles and Guidance,2009,29(1):15-17.(in Chinese)
[4]刘欣,杨涛,张青斌.助推-滑翔导弹弹道优化与总体参数分析[J].弹道学报,2012,24(3):43-48.LIU Xin,YANG Tao,ZHANG Qing-bin.Trajectory optimization and parameter analysis for boost-glide missile[J].Journal of Ballistics,2012,24(3):43-48.(in Chinese)
[5]李连仲.远程弹道导弹闭路制导方法研究[J].系统工程与电子技术,1980(4):1-17.LI Lian-zhong.Research on the close-guidance of the long-distance ballistic missile[J].Systems Engineering and Electronics,1980(4):1-17.(in Chinese)
[6]龙乐豪.弹道导弹与航天丛书-总体设计[M].北京:中国宇航出版社,2005:353-357.LONG Yue-hao.Ballistic missile and spaceflight series,collectivity design[M].Beijing:China Astronautic Publishing House,2005:353-357.(in Chinese)
