基于GA/LM混合优化的直升机全机配平算法

吴超，谭剑锋，王浩文，倪先平

(1.南京航空航天大学直升机旋翼动力学国家级重点实验室，江苏南京210016;2.清华大学 航天航空学院，北京100084)

0 引言

直升机配平是空气动力学、飞行动力学和旋翼动力学分析的基础，对直升机姿态响应计算、稳定性分析及飞控系统的设计与开发都具有重要作用。直升机配平问题为多元非线性方程组求解问题，通常需通过数值求解得到。直升机配平传统采用牛顿法［1］，该方法简单、高效，但需根据飞行状态采用不同的简化模型计算初值。文献［2］根据初始预测值将配平分为纵向、横向和旋翼转速三部分，该算法比较复杂，且需引入阻尼项构建一个依赖工程经验的算法。文献［3］采用广义简约梯度优化法，但该算法配平结果依赖于初值，且易收敛到局部最优解。文献［4］综合了梯度下降法和拟牛顿法，一定程度上降低了配平结果对初值的依赖，但该算法涉及大量偏导数，因而计算量偏大。文献［5］将浮点遗传算法计算的全局较优解作为拟牛顿法的初值，而后计算最优配平解，虽不依赖于初值，但解空间偏大，因而以一定概率收敛到非物理配平解。

非线性方程组解的存在性及唯一性仍未完全解决［6］，虽然直升机配平全局数值解并不唯一，但直升机稳定飞行状态是存在的，因而直升机优化配平解必须为物理解。本文在取值范围约束和非线性约束的条件下，将遗传算法(GA)计算的全局较优解作为LM(Levenberg-Marquardt)算法的初值，利用LM算法快速计算物理最优解，由此建立基于GA/LM混合优化算法的直升机全机配平方法。

1 飞行动力学模型

直升机飞行动力学模型是配平算法的基础，典型的气动力部件包括旋翼、尾桨、尾翼及机身等部分。

1.1 旋翼动力学模型

为突出配平算法研究，本文采用均匀入流模型和刚性桨叶假设。由挥舞铰力矩平衡得到旋翼挥舞动力学方程［7］:

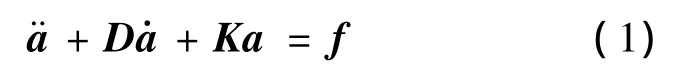
式中，a=［a0，a1，b1］T为一阶谐波形式的挥舞运动系数;D，K分别为阻尼和刚度矩阵;f为外力向量，是前进比μ、入流比λ、机体角速度、角加速度以及操纵输入的函数。

将所有桨叶的叶素气动载荷沿半径和方位角积分，并投影到机体坐标轴系下，得到桨榖六力素:

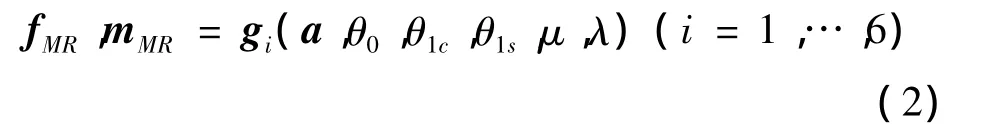
式中，θ0，θ1c和 θ1s分别为总距和两个周期变距;λ 隐含在旋翼入流方程中。

1.2 尾桨动力学模型

尾桨无周期变矩且锥度角为常值［8］。与主旋翼桨毂六力素相似，尾桨六力素:

式中，aTR，θ0TR，μTR和 λTR分别为尾桨挥舞运动向量、尾桨桨距、尾桨前进比和入流比;λTR隐含在尾桨入流方程中，尾桨挥舞运动向量可通过尾桨挥舞运动方程来计算。

1.3 尾翼和机身动力学模型

平尾、垂尾的升力和阻力分别为:

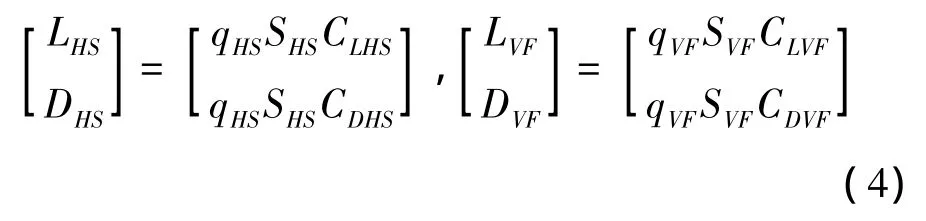
式中，qHS，qVF分别为平尾和垂尾处的动压;SHS，SVF分别为平尾和垂尾的面积;CLHS，CLVF分别为平尾和垂尾的升力系数;CDHS，CDVF分别为平尾和垂尾的阻力系数。对于采用全动平尾的UH-60A黑鹰直升机，假设平尾安装角仅是前进比的函数，并由飞测数据［9］拟合得到，垂尾安装角为零。

由于机身没有精确的理论模型，因此本文根据风洞吹风试验数据［9］计算机身六力素fF。

1.4 全机重力模型

将全机重力投影到机体坐标系下可得fG。

1.5 全机飞行动力学模型

全机动力学方程如下:

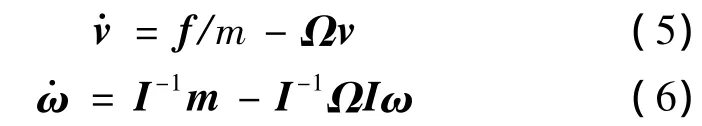
式中，v=［u，v，w］T和 ω =［p，q，r］T分别为线速度和角速度;f和m分别为合外力和合外力矩;I为全机惯性矩阵;Ω为叉乘向量算子。定义如下:

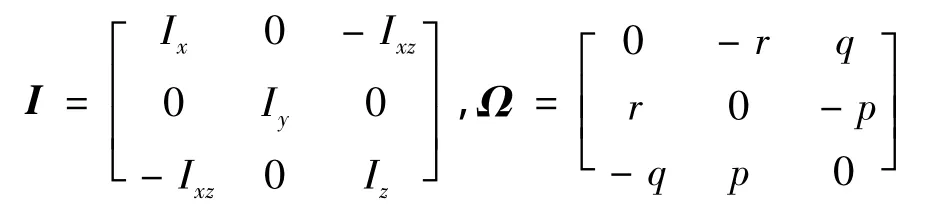
运动学方程为:

式中，α=［φ，θ，ψ］T为欧拉角;E 为角速度至欧拉角速度的转换矩阵，定义如下:

式(1)和式(5)～式(7)构成了直升机的非线性状态方程组:

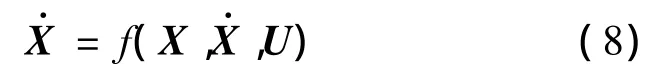
2 配平算法

2.1 配平定义和对应初始条件

配平状态对应于状态量导数为常数或零且操纵输入为固定值的状态。直升机稳定飞行时为零为定值。若为非零常数，则α将随时间线性变化，由此直升机稳定状态包含了悬停、匀速平飞、匀速直线爬升、螺旋爬升及稳定自转下滑等状态，具有广泛的意义。

由于稳定飞行时的机体角加速度为零，式(1)退化为:

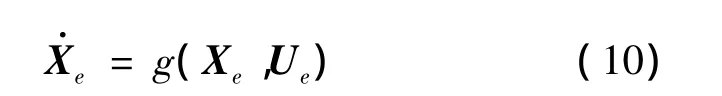
式中，下标 e表示平衡状态;Xe=［ve，ωe，αe，ae］T为配平状态量;Ue为配平操纵量。

状态方程式(10)由12个非线性方程构成，而待求变量包含12个状态量和4个控制量，为得到唯一确定解，需给定4个运动约束量［2］:飞行速度VT、爬升角γ、转弯速率和侧滑角βe。这4个量的不同组合对应了不同的稳定飞行状态，如表1所示。

本文将16个未知量分为9个独立变量XI和7个依赖变量 XD(ve，ωe，θe)。依赖变量是独立变量和运动约束量的函数，将锥度角和周期挥舞系数作为独立变量，如表2所示。

表1 稳定飞行状态和运动约束量对照表Table 1 List of motion constraints corresponding to steady state

表2 独立变量和依赖变量表Table 2 Independent variables and dependent variables

构造目标函数:

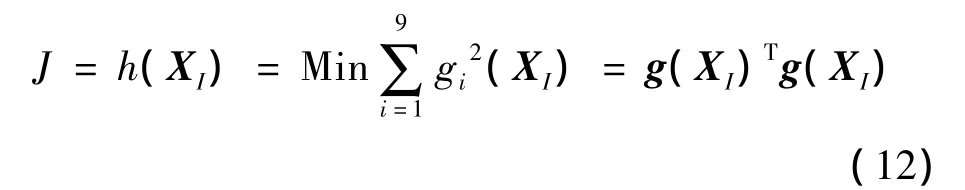
当J=0时，XI为式(11)的精确解，由此将直升机配平问题转化为优化问题，即寻找XI使得J最小。

2.2 GA/LM混合优化算法

2.2.1 解空间的确定

为避免优化算法收敛到非物理配平解，本文将构建配平解空间约束条件。对UH-60A而言，旋翼总距范围为［9.9°，25.9°］，纵向周期变距范围为［－8.0°，8.0°］，横向周期变距范围为［－ 12.5°，16.3°］，尾桨范围为［4.5°，36.5°］［9］，旋翼挥舞角范围为［－ 6°，25°］［10］，俯仰角和滚转角范围为［－90°，90°］，则配平解空间约束条件可表示为:

2.2.2 GA/LM 混合算法

依据遗传算法，本文将目标函数式(12)作为适用度函数，设定种群数ΝP=100，交叉概率pc=0.8，变异概率pm=0.2，迭代次数N=100，数值精度为双精度。

计算步骤如下:

(1)在式(13)解空间范围内随机产生ΝP个个体;(2)将十进制个体转变为二进制;(3)选择操作:利用适应度优的生存概率大，采取轮盘赌方式选择适应度优的个体(适用度函数小);(4)交叉操作:在种群中随机选出两个个体，随机确定交换位置交换基因，得到新一代个体;(5)变异操作:个体中的某一个基因以一定概率发生变异;(6)根据式(12)计算十进制个体的适应度，若达到收敛精度，则将最新一代适应度最优的个体作为LM算法的初值，否则跳回到步骤(2)继续计算。

在GA给出的较优解基础上求解式(12)，目标函数为平方和函数，可得到雅可比矩阵，将其代入牛顿法得到高斯牛顿法，但高斯牛顿法需计算在当前步k的逆，可能出现不可逆现象。为此LM算法增加了系数阻尼矩阵［11］，求解得出自变量的增量，其中λk为阻尼系数，I为单位矩阵。由此计算出，依次迭代直至达到收敛精度。LM算法的搜索方向是牛顿高斯和最速下降法方向的混合，当λk=0时搜索方向ΔXIk与高斯牛顿法相同;当λk→∞时搜索方向ΔXIk与最速下降法相同。

GA算法全局搜索性能好，不易陷入局部最优解，且易并行化［12］，但当平均适应度函数和最佳适应度函数相差较小时，GA算法寻优速度非常缓慢。为提高收敛速度，将GA给出的较优解作为LM的初值，利用LM算法快速收敛性提高直升机优化配平速度。由此，本文通过结合GA和LM算法各自优点建立了适用于直升机配平的高效全局优化算法，计算流程如图1所示。

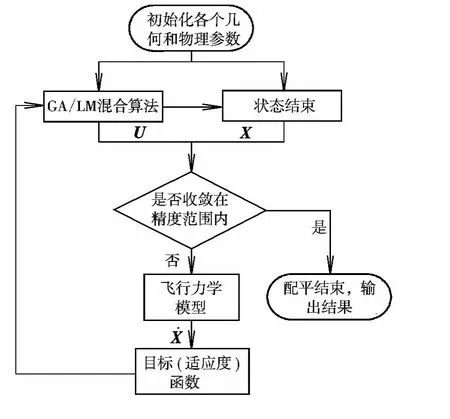
图1 主程序流程图Fig.1 Main program flow chart

3 计算结果与分析

3.1 物理最优解和常用优化算法对比

对式(12)无约束优化的求解，采用了8种单一优化算法。UH-60A以20 m/s作无侧滑的平飞，初值Ⅰ:θ0=22.92°，θ1c= － 0.57°，θ1s=4.58°，θ0TR=21.03°，其余初值为0;初值Ⅱ均为零。计算结果如表3和表4所示。

从表3和表4中可以看出，单形调优法总迭代步数较多，且该算法收敛速度依赖于初值选取;拟牛顿法和最速下降法收敛速度极快，但均对初值要求较高;BFGS拟牛顿法对初值要求较低;LM算法收敛速度最快，信赖域反射法收敛速度次之;模拟退火算法和无解空间约束的遗传算法均不收敛，不适用于直升机配平问题。

表5中给出了达到收敛精度算法的独立变量值XI。对于初值Ⅰ，单形调优法、BFGS拟牛顿法、LM法和信赖域反射法均收敛到表5中的解1;对于初值Ⅱ，BFGS拟牛顿法、LM法和信赖域反射法数值均收敛到表5中的解2。从表5中可以看出，存在两个数值解，因此目标函数收敛是直升机配平的必要条件而非充要条件。根据式(13)的解空间易知解1是配平解。

表3 优化计算结果对比1Table 3 Results of optimization algorithm part 1

表4 优化计算结果对比2Table 4 Results of optimization algorithm part 2

表5 配平值(°)Table 5 Results of trim

图2和图3为随机一次GA/LM混合算法的初值和快速收敛计算的迭代曲线图，混合算法在解空间范围内经多次计算均收敛到解1。图2反映GA算法在解空间内能很快计算出给定精度的初值，解空间约束的引入改善了无约束GA算法的收敛性，加快了收敛速度。图3说明了LM算法的快速收敛性，最终目标函数J=6.6×10－30。显然可以看出，采用GA/LM混合算法进行约束优化求解直升机的配平问题是有效的。

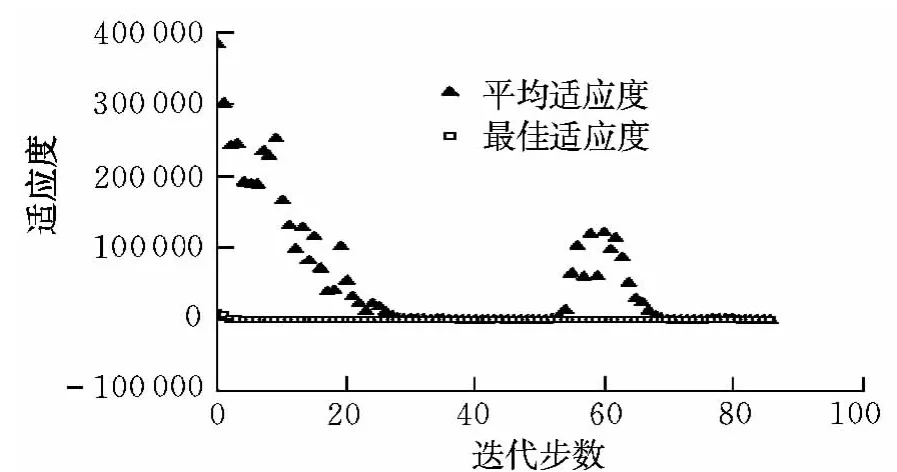
图2 初值计算迭代曲线Fig.2 Iterative curve of initial value

图3 快速收敛迭代曲线Fig.3 Iterative curve of fast convergence

3.2 算例验证和分析

协调转弯是最典型的稳定飞行状态。本文对UH-60A以51.44 m/s在1600 m高度的水平面内作不同转弯速率的协调转弯进行配平计算，并将4个操纵量转换为操纵杆位置［9］。采用GA/LM混合算法计算的配平曲线如图4～图8所示。

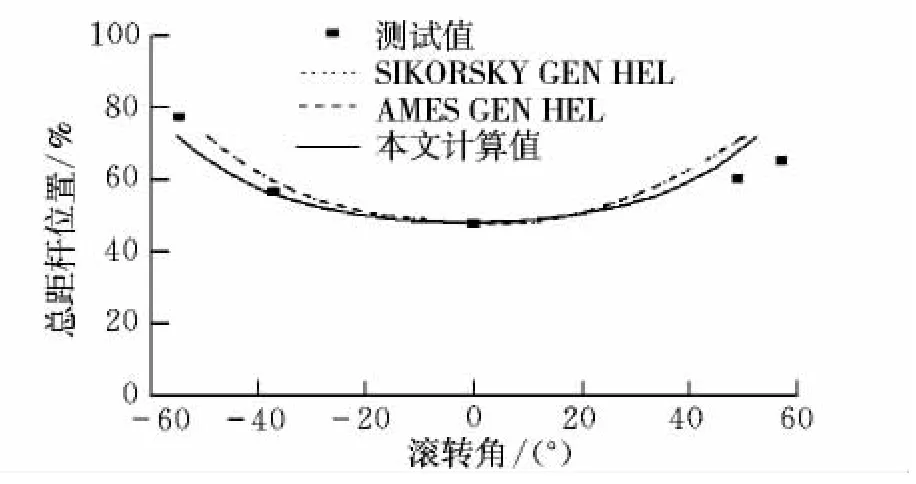
图4 总距杆协调转弯配平曲线Fig.4 Trim results of collective lever for coordinated turn

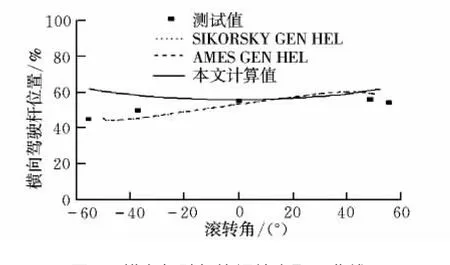
图5 横向驾驶杆协调转弯配平曲线Fig.5 Trim results of lateral stick for coordinated turn

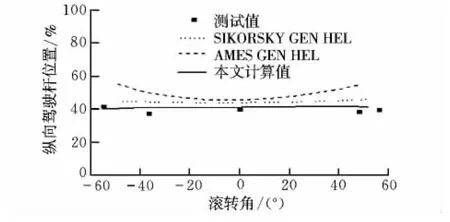
图6 纵向操纵杆协调转弯配平曲线Fig.6 Trim results of longitudinal stick for coordinated turn

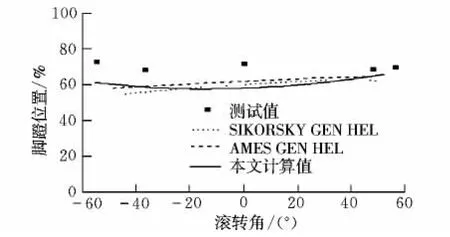
图7 脚蹬协调转弯配平曲线Fig.7 Trim results of pedal for coordinated turn

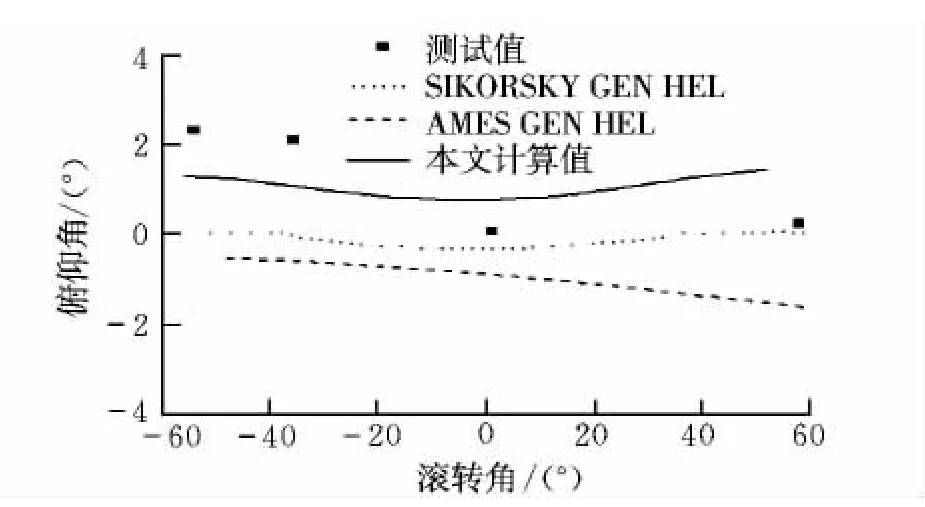
图8 俯仰角协调转弯配平曲线Fig.8 Trim results of pitch angle for coordinated turn

从图4～图8中可以看出，本文计算的总距和脚蹬与GEN HEL［13］计算值比较吻合;由于全动平尾的安装角是由实验数据给出，因此本文计算的纵向操纵杆和俯仰角比GEN HEL计算值更接近飞测数据;横向驾驶杆在较大负滚转角时与试验数据有较大误差，主要原因是脚蹬位置与试验数据存在一定的静态误差。

本算例计算中假设侧滑角为零，而飞行测试时飞行员很难保证，因此在受侧滑角影响明显的横向方向上，本文计算结果与飞行测试结果存在一定偏差。

4 结束语

在直升机动力学模型基础上，通过构造优化目标函数，将直升机全机配平问题转化为优化问题。针对单一优化算法对初值依赖高，易收敛到非物理解问题，构建了解空间约束条件，提出了一种基于GA/LM混合优化的直升机配平算法。通过UH-60A直升机对协调转弯的计算，表明本文所建立的混合优化算法准确高效，且不依赖于初值，适用于直升机配平分析。

［1］ 高正，陈仁良.直升机飞行动力学［M］.北京:科学出版社，2003:65-71.

［2］ Padfield G D.Helicopter flight dynamics:the theory and application of flying qualities and simulation modeling［M］.Oxford:Blackwell Publishing Ltd，2007:192-204.

［3］ Schank T C.Optimal aeroelastic trim for rotorcraft with constrained non-unique trim solutions［D］.Atlanta:Georgia Institute of Technology，2008.

［4］ Subramanian S，Gaonkar G H，Maier T H.A theoretical and experimental investigation of hingeless-rotor stability and trim［C］//Twenty-Third European Rotorcraft Forum.Dresden，Germany，1997:10.

［5］ 代冀阳，吴国辉，朱国民.适于直升机配平计算的混合遗传算法［J］.飞行力学，2010，28(1):24-28.

［6］ 李广杨，关治，白峰杉.数值计算原理［M］.北京:清华大学出版社，2000:243.

［7］ Talbot P D，Tinling B E，Decker WA，et al.A mathematical model of a single main rotor helicopter for piloted simulation［R］.NASA-TM-84281，1982.

［8］ Hilbert K B.A mathematical model of the UH-60 helicopter［R］.NASA-TM-85890，1984.

［9］ Howlett J J.UH-60A black hawk engineering simulation program［R］.NASA CR-166309，1981.

［10］ Cross J，Brilla J，Kufeld R，et al.The modern rotor aerodynamic limits survey:a report and data survey［R］.NASATM-4446，1993.

［11］龚纯，王正林.精通MATLAB最优化计算［M］.北京:电子工业出版社，2012:213-216.

［12］张呈林，郭才根.直升机总体设计［M］.北京:北京国防工业出版社，2006:141-143.

［13］ Ballin M G.Validation of a real-time engineering simulation of the UH-60A helicopter［R］.NASA-TM-88360，1987.