重装空投多刚体系统动力学建模与仿真

王晖，唐硕，张久星，张登成

(1.西北工业大学航天学院，陕西西安710072;2.空军工程大学航空航天工程学院，陕西西安710038)

0 引言

重装空投是指通过大中型运输机将重型货物运输到指定区域，并利用降落伞等减速装置降落到地面的空投技术［1］。它既是军队实现快速反应和远程机动的关键手段，又是后勤保障和持续支援的重要工具。

重装空投系统是一种复杂的动力学系统，相关领域学者提出了许多建模方法［2-5］，大体可归纳为分离法和整体法两类［6］。分离法是将货物的运动作为对飞机的扰动进行建模，整体法则是把飞机和货物作为一个整体，两者之间的作用视为内力进行建模。实际建模中两种方法极易混淆，不同阶段模型的受力和状态量确定也容易造成混乱。拉格朗日方法第二类方程作为一种程序化的建模方法，可不忽略系统中的理想约束，使得重装空投系统的建模非常简单，同时假设条件宽泛，模型精度较高，结构紧凑，更便于仿真计算。

1 基于拉格朗日方法的重装空投动力学模型

重装空投系统包括载机、货物和牵引伞。为了简化推导过程，避免求解物体间的约束力，本文采用拉格朗日方法进行建模。重装空投系统组成见图1。

图1 重装空投系统示意图Fig.1 Schematic diagram of the heavy-equipment airdrop system

为了简化计算作如下假设:

(1)飞机和货物的质心位于舱板平行的同一平面上，距离为l;

(2)载机和货物质量分别为m1和m2，且质量均匀分布;

(3)伞简化为牵引力，方向与气流轴xa轴相反;

(4)货物沿导轨移动，无横向运动。

第二类拉格朗日方程为:

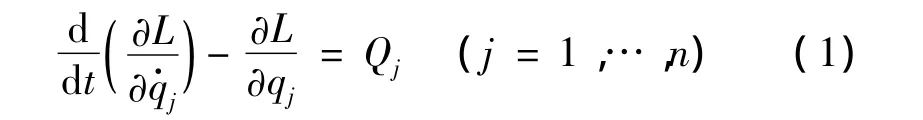
广义坐标为:

载机质心速度和角速度为:

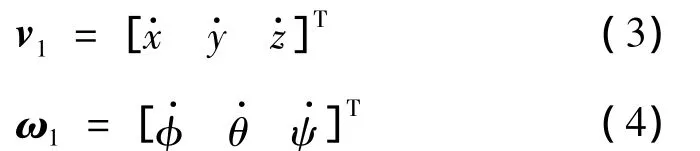
载机动能为:

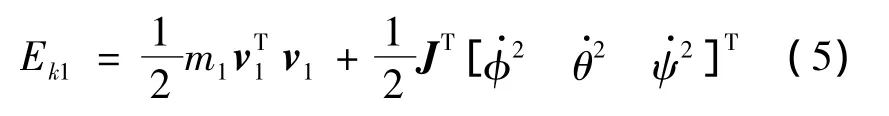
货物在地面坐标系的质心位置(以飞机右偏航为例)为:

其中:

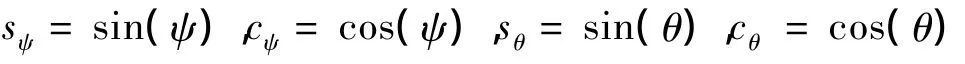
货物的速度为:

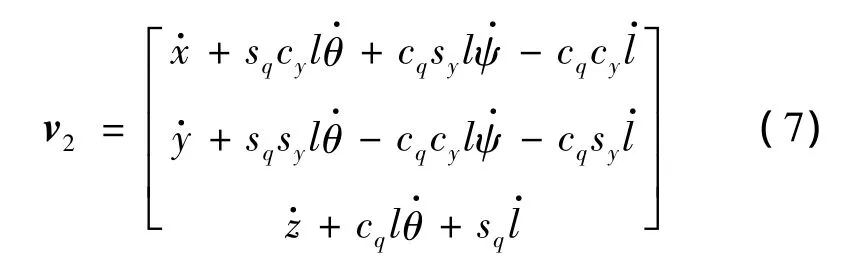
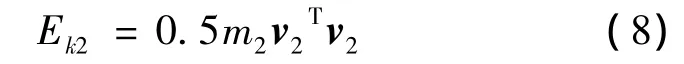
重装空投系统的总动能为:

定义地平面为零势能位置，则重装空投系统的势能为:

于是可得拉格朗日函数为:

货物的动能为:

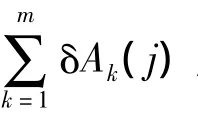
于是可求得广义力为:

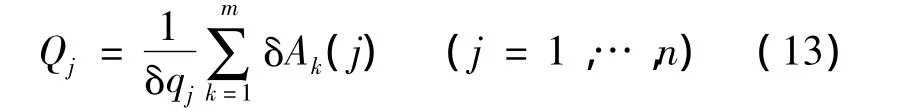
空投系统所受的外力主要有:沿体轴的发动机推力P，沿气流轴的空气动力(X，Y，Z)，沿气流轴方向的牵引伞拉力N、重力G1和G2。

发动机推力沿地轴系投影，可得:

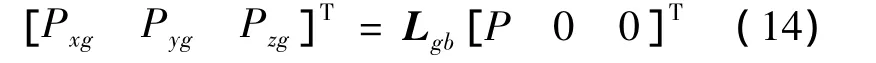
假设飞机无侧滑，空气动力沿地轴系投影，可得:

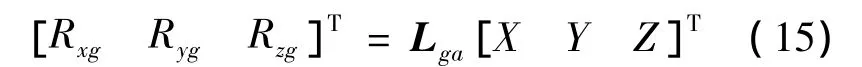
牵引伞拉力沿地轴系投影为:

牵引伞拉力沿飞机体轴系投影为:

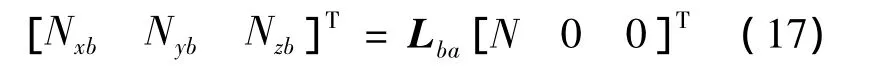
于是，可得广义力为:

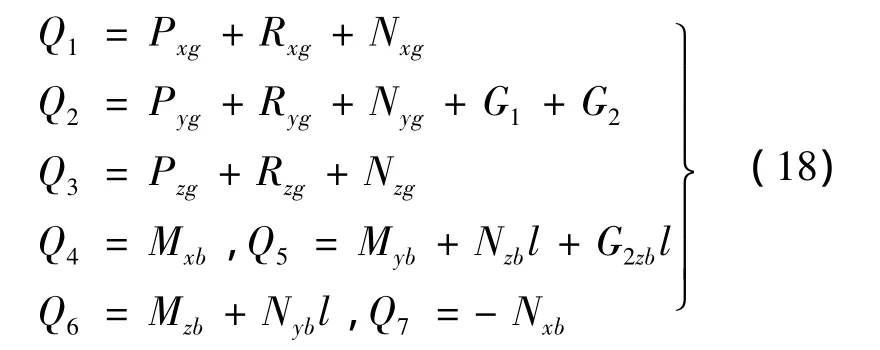
将式(2)、式(11)和式(18)带入式(1)，可得矩阵形式的动力学模型为:

其中:

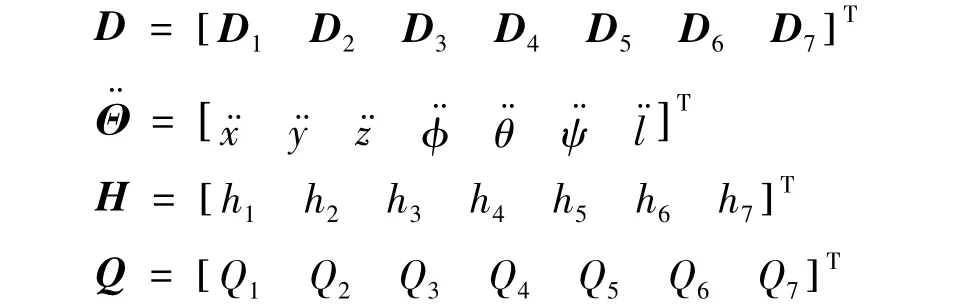
上式的D和H中:

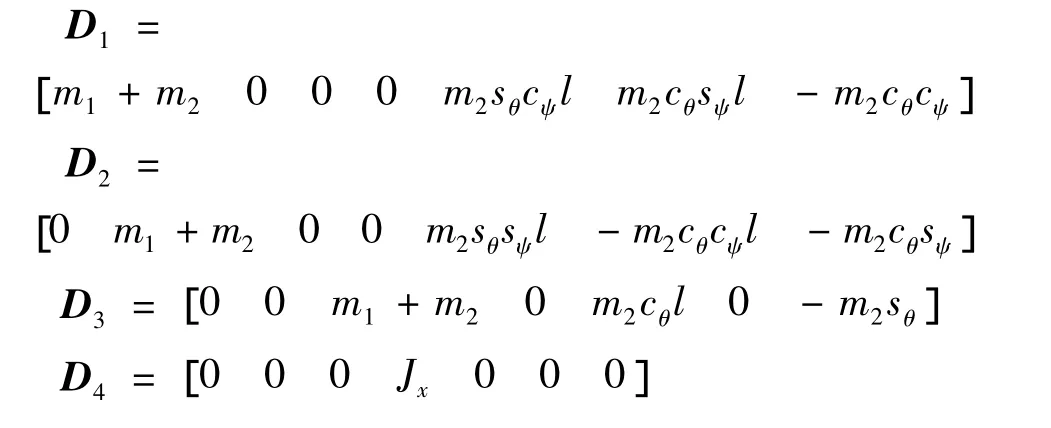
方程右端含有变量迎角α和侧滑角β，为了求解方程还需补充以下方程:

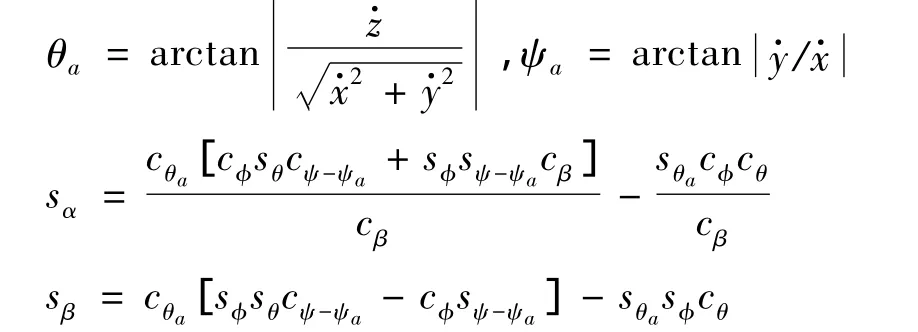
至此，重装空投系统模型建立完毕。通过Matlab编写仿真程序即可完成重装空投的仿真。

2 基于ADAMS的重装空投仿真模型

2.1 重装空投三维实体建模

根据载机、货物和降落伞的几何参数，采用三维CAD软件CATIA，逐一建立机身、机翼、垂尾、发动机等各零/部件以及货物和降落伞的三维实体模型，并装配完成重装空投系统的三维实体模型，如图2所示。将模型导入ADAMS，并为载机和货物添加质量特性。

图2 重装空投三维实体模型Fig.2 Three dimensional solid model of the heavy-equipment airdrop system

2.2 载机的约束力

载机和货物的耦合作用主要体现在货物沿导轨移动与载机俯仰运动的相互作用。为简化模型，可将载机通过旋转副与大地连接，并在旋转副上施加旋转驱动，用来模拟载机的俯仰气动力矩以及驾驶员操作飞机抵抗货物干扰的低头力矩。

2.2.1 载机俯仰气动力矩

载机俯仰气动力矩通过CFD计算得到。首先将CATIA建立的载机模型去掉尖角后导入ICEM进行网格剖分，然后将网格导入Fluent进行数值仿真。如图3所示，湍流模型选择Spalart-Allmaras模型。将计算结果导入Matlab通过差值函数法进行拟合后，可获得载机的俯仰气动力矩系数。再将载机的参考面积S、对应的力臂值L、空气密度ρ和实际来流速度V，以及仿真所得的气动参数Cm值代入式(21)，即可计算出载机的俯仰气动力矩:

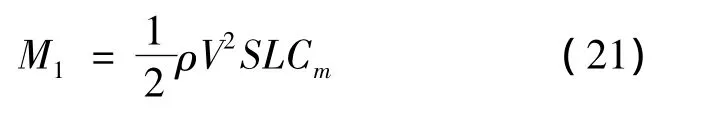
图3 载机计算网格Fig.3 Computing grid of the carrier

2.2.2 载机低头力矩

驾驶员操作下产生的低头力矩主要用于补偿因货物重心后移造成的抬头力矩，二者大小相当。力矩表达式为:

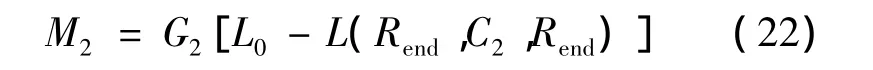
式中:G2为货物重力;L0为导轨的长度;表达式L(Rend，C2，Rend)为货物重心(C2)到导轨末端(Rend)在导轨坐标系中的距离;L0－L即货物距离载机重心的距离。该力矩施加时间需考虑驾驶员反应的延迟时间。

2.3 载机和货物之间的相互作用力

载机和货物间的作用力可通过建立接触力实现［7］。涉及到的货物和传送轮胎之间接触力的相关数据，如接触摩擦系数、阻尼等，均在创建接触面板中设置。

2.4 牵引伞的气动力

牵引伞的动力学方程可以利用克希霍夫运动方程推导得到。克希霍夫运动方程的矢量形式为:

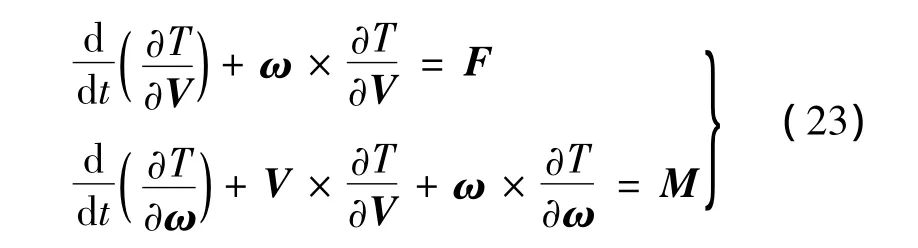
式中:T为伞-流体系统动能;V为速度;ω为角速度;F为外力;M为外力矩。文献［8］依据上述方程推导给出了伞体坐标系下的标量动力学方程。根据其推导结果，结合本文假设条件，可得到牵引伞动力学方程如下:

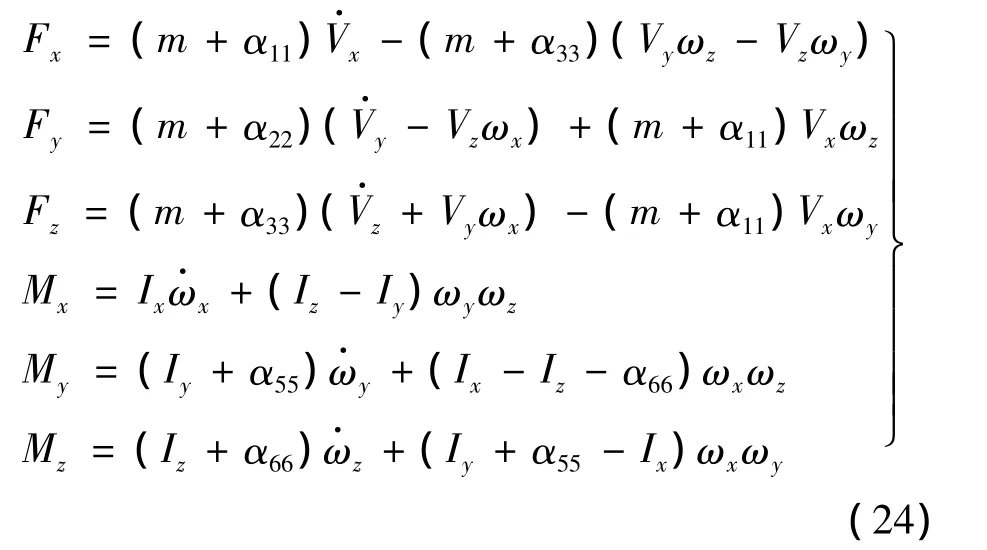
式中:m为牵引定伞质量;Ix，Iy和Iz为相对于伞体轴的转动惯量;α11，α22和 α33分别为沿伞体系 Xb，Yb和Zb三个轴的附加质量，且 α22=α33;α55和 α66分别为沿伞体系Yb和Zb轴的附加转动惯量，且α55=α66。以上常量均可参阅文献［8］进行求解，其他变量通过ADAMS/View自带的测量工具测得，测量点选为牵引伞的气动压心。

3 仿真分析

对所建立的模型分别进行仿真，初始条件设置如表1所示。表中:H为载机初始高度;V为载机的初始速度;θ为载机初始俯仰角;m2为货物的质量;L为货物距载机重心的初始距离;Dp为牵引伞的阻力特征;t为牵引伞打开时刻。

表1 仿真初始条件Table 1 Initial conditions of the simulation

仿真结果如图4～图6所示。其中模型1为多刚体系统动力学模型并加入了简单的控制律;模型2为商业软件建立的仿真模型。

从仿真结果可以看出:2 s时牵引伞打开，载机受开伞载荷的影响，高度、速度均有所下降，同时，随着货物的后移，载机的俯仰角逐渐增大;随后，在控制系统作用下，对飞机施加低头力矩，飞机俯仰角持续增大到峰值后开始减小;3 s左右，货物掉落，相当于载机质量突然减轻，载机的高度和速度开始逐渐升高，突然失去货物的干扰力矩，载机的俯仰角迅速下降，在控制系统的作用下又逐渐增大。

图4 载机高度变化曲线Fig.4 Altitude curve of the carrier

图5 载机速度变化曲线Fig.5 Velocity curve of the carrier

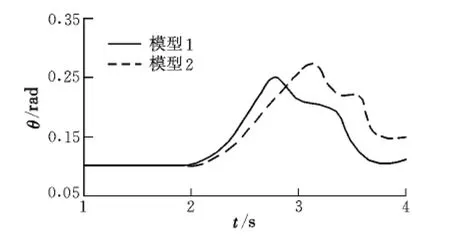
图6 载机俯仰角变化曲线Fig.6 Pitch angle curre of the carrier

从仿真数据曲线和响应特性对比数据来看，本文建立的重装空投多刚体动力学模型和商业软件建立的模型动态响应相近，且均与实际情况相符。

4 结束语

基于多刚体动力学中的拉格朗日方法和飞行力学建立了重装空投多体系统动力学模型，并采用商业软件进行了仿真对比分析。相对于采用多种商业软件联合建模仿真的繁冗方法，该模型不仅建立方法简单，假设条件宽泛，且精度较高，结构清晰紧凑，更加便于仿真计算，为下一步货物运动到载机舱板底端后绕舱板转动，以及货物与载机分离后的物伞系统建模打下了基础。

［1］ 李大东，孙秀霞，董文瀚，等.考虑多种影响因素下的改进重装空投系统建模［J］.系统工程与电子技术，2013，35(2):447-451.

［2］ Ke Peng，Yang Chunxin，Yang Xuesong.Extraction phase simulation of cargo airdrop system［J］.Chinese Journal of Aeronautics，2006，19(4):315-321.

［3］ Chen Jie，Shi Zhongke.Aircraft modeling and simulation with cargo moving inside［J］.Chinese Journal of Aeronautics，2009，22(2):191-197.

［4］ Michael Ward，Carlos Montalvo，Mark Costello.Performance characteristics of an autonomous airdrop:system in realistic wind environments［R］.AIAA-2010-7510，2010.

［5］ Thomas Jann.Coupled simulation of cargo airdrop from a generic military transport aircraft［R］.AIAA-2011-2566，2011.

［6］ 杨雨，陆宇平.运输机超低空重装空投纵向反步滑模控制研究［J］.航空学报，2012，33(12):2301-2312.

［7］ 张登成，闫杰，张久星.内装式空射运载火箭与载机分离研究［J］.弹箭与制导学报，2009，28(5):20-27.

［8］ 王利荣.降落伞理论与应用［M］.北京:宇航出版社，1997.