振弦式应变计测试混凝土线膨胀系数的研究

2014-12-25吴跃红曾世东

交通运输研究 2014年23期

吴跃红，曾世东

（西南林业大学土木工程学院，云南昆明650224）

0 引言

混凝土和其他材料一样具有热胀冷缩的特性，当温度变化时将产生体积变形，若变形受到约束将产生相应的温度应力。要计算温度应力或变形量，就必须知晓混凝土的线膨胀系数。混凝土应力现场监测中，实测应力包含了温度变形的影响，要较准确地剔除温度的影响，也必须知晓混凝土的线膨胀系数。现有研究表明[1-2]，混凝土的线膨胀系数并非定值，常温条件下，它与骨料的种类、水泥用量、含水量以及龄期等有关，大致在0.54×10-5～1.42×10-5/℃之间变动。在通常计算中，一般将混凝土的线膨胀系数取为1.0×10-5/℃，这实际上是十分粗略的，可能带来较大的计算误差。因此，研究一种能较准确地测定混凝土线膨胀系数的简便方法，具有较强的实用价值。笔者结合混凝土应力现场监测的实践，提出了一种利用埋入式应变计测试混凝土线膨胀系数的简便方法。

1 振弦式混凝土应变计的工作原理

如图1 所示，振弦式应变计由前后端座、不锈钢护管、信号传输电缆、振弦及激振电磁线圈等组成，除此之外，有的应变计还带有一个热敏电阻器，用以测试传感器周围环境温度，以便进行温度修正[3-4]。振弦式应变计的基本结构包括外部的应变筒和两端固定于应变筒的钢弦，当应变筒受力发生变形时，内部钢弦随之变形，钢弦被拉紧或松弛，其振动频率也会随之升高或降低，因此，通过测量振弦的频率变化可推求振弦的拉力变化，从而求得传感器所在点的应变变化。

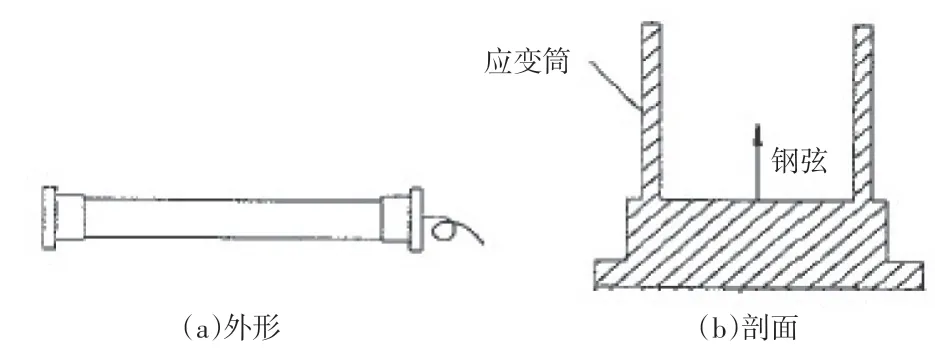
图1 振弦式应变计的基本结构

两端固定且拉紧的振弦的固有频率f的表达式为：

式中：f为弦的振动基频；T为弦的张力；ρ为弦式材料的线密度；L为弦的有效长度。

由式（1）可得：

对于同一根长度的振弦，其k值不变，弦的拉力与频率的平方成比例关系：

式中：ΔT为张力变化；f0为弦的初始频率。

假设应变筒与振弦的变形协调，因此，应变增量相同。设振弦的应变增量为εg，应变筒的应变增量为εh，则有：

式中：E为振弦的弹性模量；A为振弦的截面积；EA即为振弦的轴向刚度。

频率与应变的关系在出厂以前通过小型压力机和千分表进行标定：用压力机在应变计两端加压，每一级加压完，用千分表测量应变计端部的位移，除以钢弦的长度，即为钢弦的应变变化值，同时测量应变计的频率变化，经过多级加载，可绘制f（频率）—ε（应变）关系曲线，进行回归拟合，确定比例系数，从而得到频率f与应变ε的对应关系。

2 混凝土线膨胀系数测试方法

在现场制作100mm×100mm×515mm 的素混凝土矩形试件，中部埋入1 支带测温功能的振弦式混凝土应变计（型号为JMZX—215AT），如图2所示。

图2 混凝土试件示意图（单位：mm）

为了防止混凝土浇筑过程中应变计歪斜，采用细铁丝作支架，将应变计固定于试模内。混凝土试件浇筑24h后脱模，将试件移入室外，接受太阳辐射和气温的影响。为了使试件沿截面方向能产生较均匀的温度场，将试件竖置，并定期旋转试件，使其均匀受温。在室外条件下，试件受太阳辐射和气温影响，温度和测读应变均产生周期性变化。由于试件尺寸较小，可以近似认为试件温度变化均匀，测读应变的变化既包括温度引起的测读应变，又包括混凝土干缩湿胀引起的测读应变。图3 为某混凝土试件2d 内的温度—应变典型变化曲线。

图3 混凝土试件温度和测读应变之间的典型变化曲线

由应变计的原理可知[5]，当混凝土凝固之后，由于混凝土的模量远大于应变筒的变形模量，因此，钢弦的变形取决于混凝土的变形。如混凝土的线膨胀系数小于钢弦的线膨胀系数，当温度升高时，钢弦的伸长将受到变形量较小的混凝土的约束，表现为受压应变；反之，当温度降低时，钢弦的缩短将受到约束，表现为受拉应变。单位温度变化的影响量，取决于混凝土和钢弦线膨胀系数的差值，如钢弦线膨胀系数已知，则能求得混凝土线膨胀系数。

由图3可见，应变曲线的峰值和温度曲线的峰值一一对应，一般约在前一天上午7：00 左右，试件温度达到最低值tmin1，测读应变达到极小值εmin1（指绝对值，应变计应变表现为受压为负，受拉为正），下午6：00 左右，试件温度达到最高值tmax1，测读应变达到极大值εmax1；第二天上午7：00 左右，试件温度再次达到最低值tmin2，测读应变达到极小值εmin2。在一个循环周期内，温度对测读应变的影响系数分别为：

由于前一天上午7：00～下午6：00、下午6：00～第二天上午7：00 这两个时段内的混凝土收缩应变值可认为基本相等，取α1和α2的平均值刚好可以消除收缩应变的影响。则温度对测读应变的影响系数为：

αt实质上是由于混凝土和钢弦线膨胀系数的差异引起的，已知钢弦的线膨胀系数αg=12.2με/℃，则试件的线膨胀系数α=αt-αg=(12.2-αt)με/℃。根据上述公式，则容易求得混凝土试件的线膨胀系数。

3 测试方法准确性的验证

在龄期约为15d时，采用上述方法测试了混凝土线膨胀系数，其中tmin1、tmax1、tmin2分别为17.7℃、28.7℃、17.2℃，εmin1、εmax1、εmin2分别为-241με、-290με、-251με，根据式（5）～式（7）计算得到混凝土的线膨胀系数α=8.28με/℃。随后设计了1个对比试验进行验证。

在该混凝土试件外面缠绕电热带进行加热，并在试件外浇筑聚氨脂泡沫保温层。为了保证试件能自由伸缩，在试件下方设置可动滚轴，在试件两端中心处水平安置千分表，直接测试升温作用下混凝土试件的膨胀量，具体如图4所示。

图4 电热带加热混凝土试件示意图

根据膨胀量和试件长度可计算得到试件的应变值，温度变化与应变变化的关系如图5所示。

图5 温度变化与应变变化关系图

由图5可见，采用直接加热法测得的混凝土线膨胀系数α=8.59με/℃，与本文方法所得结果（α=8.28με/℃）较为接近，验证了本文方法测试结果可信。而且，与直接加热法相比，本文的方法操作更为简单。

4 混凝土线膨胀系数测试结果分析

采用本文方法，对该混凝土试件进行了长达230d 的应变测试，得到的混凝土线膨胀系数随龄期变化情况如图6所示。

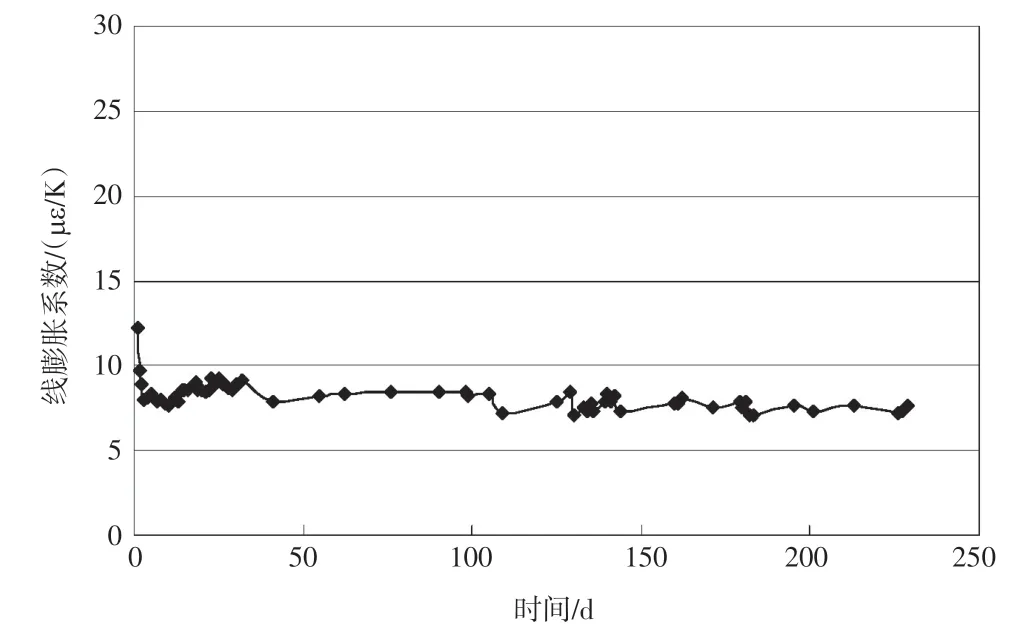
图6 混凝土试件线膨胀系数随龄期变化结果

由图6 可见，在早龄期（2～3d），混凝土的线膨胀系数的变化较为剧烈，呈现大幅减小的趋势，主要原因是早期混凝土的含水量高，而水的膨胀系数远大于混凝土的膨胀系数；大约3d 后，线膨胀系数趋向均匀，并略有减小，变化规律与现有研究成果一致[1，6]。取3d后的线膨胀系数进行简单平均，得到混凝土试件的平均线膨胀系数为8.08με/℃，比《公路桥涵设计通用规范》（JTG D60—2004）推荐的值（10με/℃）小。