起伏地表检波器组合响应

王志强，韩立国，巩向博，凌 云

吉林大学地球探测科学与技术学院，长春 130026

0 引言

随着地震勘探的不断发展，对野外勘探资料的信噪比和分辨率的要求越来越高，勘探对象也逐渐转向一些特殊地形。特殊地表条件所涉及的对象包括海陆过渡带、山前地带、沙漠地区、黄土塬覆盖区、沼泽湖泊、工矿城镇等［1－3］。在这些地区，由于地表条件复杂、各种干扰比较发育，检波器组合经常被作为提高野外资料信噪比的重要手段。

Parr等［4］研究了检波器组合对水平旅行波的衰减能力，对比了不同检波器数的线性组合的特征，以及检波器组合响应的随方位变化特征；Rigdon等［5］使用变偏移距数据对比了不同长度的线性组合特征，计算了频率域中不同组合形式接收的数据信噪比；Aldridge［6］研究了地表速度随机变化的影响以及组合中单个检波器对入射波、P波和S波的响应特征；Regone［7］基于信噪比理论将一系列已知滤波水平的组合滤波器应用到原始数据中，研究了切比雪夫加权组合的特性；Hoffe等［8］研究了基于叠后数据振幅谱的检波器组合特性，并发现由于近地表厚度变化较大，如果不应用静校正检波器组合对于单道记录效果并不好。

检波器组合就是在一个地震道将多个检波器按照一定的形式排列起来并同时接收地震波，然后将它们接收到的信号叠加起来作为同一地震道的输入［9－10］。它是根据信号传播到组合时的视速度的差异，削弱相干或不相干噪声来增强有效信号，最终将有效信号和噪声区分开来的。由于有效波和干扰波信息同时存在于地震信号中，面波等干扰波一般是沿地表传播的，而有效波来自于地下深处，且近于垂直地表传播；通过调整检波器组合的组内距，使面波到达2个检波器的时差是其视周期的一半，从而使面波的合成振幅几乎为0，而反射波振幅要比组合前增大一倍，使资料的信噪比大大提高［11－13］。

检波器组合形式多种多样，有线性组合、面积组合，等灵敏度组合、不等灵敏度组合等，但无论哪种组合形式都以简单的线性组合为基础。笔者以检波器面积组合为主，讨论其在起伏地表条件下的组合特性，并对比通过组合滤波后有效波与干扰波的响应情况，从而看出通过检波器组合滤波后资料信噪比得到了提高。

1 检波器组合响应原理

将一组检波器组合放在笛卡尔坐标中，原点设在检波器组合的中心，并且以沿排列方向作为x轴，以垂直排列方向作为y轴，组合中第i个检波器的位置就可以表示为下式：

式中：xi、yi表示单个检波器的坐标；I、J表示x轴和y轴方向的单位向量。则单个检波器的波数响应可以用δ函数的二维空间傅里叶变换表示为［14］

即

式中：k表示波数；kx、ky分别表示x轴和y轴方向的波数分量；Ai（k）表示第i个检波器的波数响应；j

再将组合中所有检波器的响应相加到一起，就可以得到N个检波器组合整体的响应［15］：

以上是水平地表条件下的检波器组合响应原理，但实际施工中经常要将检波器组合布设在斜坡带上或更复杂的地形上。采用等效变换的方法，将斜坡带检波器组合等效变换到水平面上进行组合响应的计算［16］。斜坡带上的检波器组合等效变换到水平面上的基本原理：假设地震波的波前面在检波器组合所分布的面积内近于平面，在地震信号的形式不变、检波器是等灵敏度的情况下，组合的方向特性取决于波到达组内检波器的时差，所以可以将倾斜面与地震波前交线上的检波点沿着波前面移动到与之时差相同的波前面与水平面的交线上，这样就可以把倾斜面上检波器组合响应等效为水平面上检波器组合的响应。

假设有一倾斜地表，倾角为φ，A、B为斜坡带上的2个检波点，干扰波以入射角α沿着倾斜地表的上倾方向传播，如图1a所示。波前面首先到达检波点A，经过Δt时间后波前面又传播到检波点B，此时波前面与水平面的交点为B′，则波前面沿着倾斜地表从检波点A传播到检波点B的时间与其沿着水平面从A传播到B′的时间相等；因此，可以把倾斜地表上的B点检波器等效为水平面上的B′点进行检波器组合响应的计算。假设A、B间的距离为Δx，那么根据A、B、B′三点的几何关系，A、B′间的距离为Δx（cosφ＋sinφcotα）。按照同样的方法，可以将倾斜面上其他检波点等效到水平面上，这时就可以用水平面上的检波器组合理论进行计算分析了。当干扰波沿着倾斜地表下倾方向传播时，如图1b所示，按照同样的分析方法，倾斜面上2个检波器间的距离Δx变为Δx（cosφ－sinφcotα）［17］。

2 不同组合图形的响应

根据检波器组合响应的基本原理，可以得到不同组合图形的响应玫瑰图。图2是检波器线性组合时的响应情况：线性组合对于沿组合方向传播的干扰波（波长为λ）压制程度最大，但在垂直组合方向基本没有压制。图3是检波器面积组合的响应（以方形和圆形组合为例）。图中显示规则面积组合对于来自各方向的干扰波都有压制，且对各方向干扰波压制水平基本是一致的。当组合参数相同时，视波长较短的波的响应值较小，表明检波器组合对短视波长的干扰波压制较强。

3 起伏地表检波器方形组合响应

以方形组合为例，研究起伏地表检波器组合的响应情况。确定组内距为2m，组合的排列方向沿着倾斜地表上倾方向，利用地表的倾角不同表示地表倾斜程度的差异。对应于视波长100m和80m情况下不同组合基距的检波器组合响应玫瑰图如图4和图5所示，其中0°方位角表示组合的排列方向。

从图4和图5可见，随着检波器组合组内高差的增加（即地表倾斜角度增大）：沿着倾斜地表上倾方向传播过来的干扰波对应的组合响应值逐渐减小，说明干扰波被压制的程度逐渐变大；而沿着倾斜地表下倾方向传播过来的干扰波对应的组合响应值却逐渐增大，表明干扰波被压制的程度逐渐减小。同时，组合的响应数值变化还表明，倾斜地表对大组合基距（即检波器数量较大时）的检波器组合响应影响稍大；对比图4和图5可以看出在组合基距等参数相同的条件下，倾斜地表对较大视波长干扰波的压制效果影响稍大。综合来看，地表倾斜使得沿地表下倾方向传播的干扰波压制程度降低，降低程度与地表倾角大小、干扰波视波长、组合基距等因素有关。

以上讨论的方形组合形式都是将检波器均匀布置在地表，即在排列方向和垂直排列方向组内距相同。实际中垂直方向传来的干扰波对后期的数据处理影响较大，很难将其处理干净。为了在野外数据采集时将垂直方向的干扰波压制到最小，可以通过增大检波器组合的横向组合基距来达到目的［18－19］。

图1 干扰波沿倾斜地表上倾方向（a）和下倾方向（b）传播示意图Fig.1 Sketch map that interference wavespreadalong the up dipdirection（a）and the down dip direction（b）

图2 检波器线性组合时响应玫瑰图Fig.2 Response roses of the linear geophone array

图3 检波器面积组合时响应玫瑰图Fig.3 Response roses of the areal geophone array

图4 视波长为100m地表倾斜程度变化时检波器方形面积组合响应玫瑰图Fig.4 Response roses of square array for variable dip angle and 100mwavelength

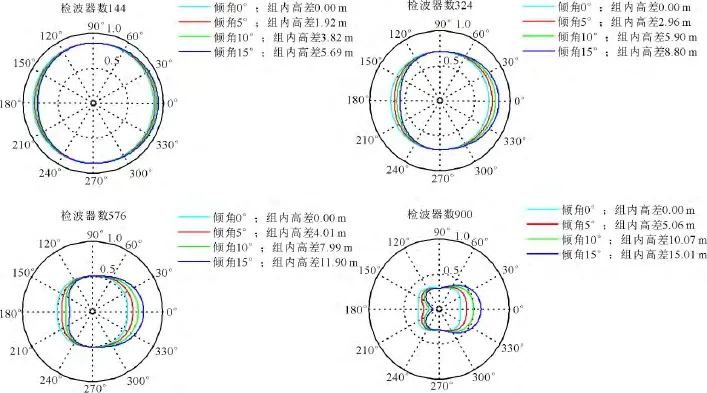
图5 视波长为80m地表倾斜程度变化时检波器方形面积组合响应玫瑰图Fig.5 Response roses of square array for variable dip angle and 80mwavelength

为方便计算，使用121个检波器组合成方形，组内距为2m，地表倾角为10°。从横向拉开不同距离时的响应玫瑰图（图6）中可以看出：当检波器组合横向拉开布设后，组合在垂直排列方向的响应值明显减小，即对来自该方向的干扰波压制增强了；当横向拉开距离为干扰波视波长时，对干扰波压制最大，响应值几乎为0。

4 有效波与干扰波的响应对比

已知某地区地表倾斜角度大约为20°，图7是该地区的一个单炮记录。该区面波干扰的视波长主要为10～30m，经过计算得该区随机干扰的相关半径为3.6m，所以检波器组合的组内距取3.6m。假设面波沿地表传播，有效波从地下深处垂直地表传播，笔者以视波长为25m的面波为例，讨论有效波视波长为40～100m时不同组合形式的响应情况。

4.1 方形组合响应

首先使用36个检波器排列成方形组合，组内距为3.6m，且排列方向沿倾斜地表上倾方向，其响应情况如图8。图9为方形组合沿垂直排列方向拉开一个视波长后的响应。

4.2 矩形组合响应

使用24个检波器排列成两排，排列方向沿斜坡带上倾方向，其相应情况如图10。

图6 检波器组合横向拉开不同距离时的玫瑰图Fig.6 Response roses of geophonearrayforlateral pulling different distances

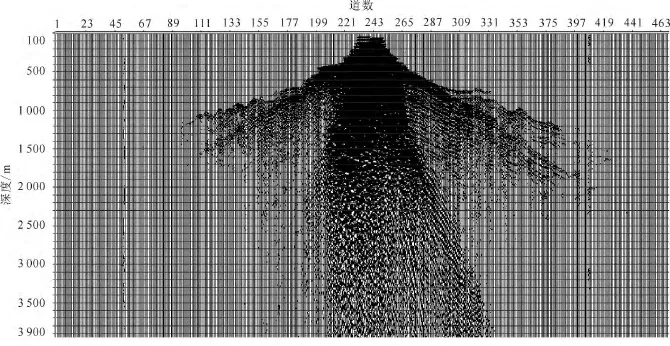
图7 单炮记录Fig.7 Shot record

图8 方形组合的响应Fig.8 Response roses of square array

图9 方形组合横向拉开一个视波长后的响应Fig.9 Response roses of square array afterlateral pulling a visual wavelength

图10 矩形组合响应Fig.10 Response roses of rectangle array

根据图8、图9和图10，能够看出通过检波器组合滤波，面波干扰的强度已得到明显压制，而有效波的强度相对增强了，大大提高了资料的信噪比。有效波视波长越小，其响应值越小，说明被压制得越严重；由图9可以看出，当方形组合在垂直排列方向拉长为一个干扰波的视波长时，干扰被压制得最严重，此时有效波也受到一定程度压制，但还是提高了信噪比。对比图8和图10可见，方形组合对各方位的压制程度基本相当，而矩形组合对沿排列方向的干扰波压制的比较严重，对于垂直排列方向干扰波则压制很小，可见规则对称的组合图形要比不对称的组合图形压制效果更佳。

5 组合参数反演优化

在野外实际施工中，检波器组合参数的选择对野外资料的结果影响较大，主要包括检波器组合图形、检波器数、组内距、组合基距、组内高差等。为了得到最佳的组合参数，可以用反演的方法对其进行优化，笔者主要用拟牛顿法（BFGS）方法实现。

优化迭代算法在反演地球物理参数中起着重要的作用。先构造一个关于要反演的地球物理参数的最优化问题，即在模型空间中寻找一个模型，让其产生的合成数据与观测数据的误差能量达到最小；然后用优化迭代算法求解出地球物理参数。BFGS方法是求解无约束最优化问题的最有效的方法之一，有良好的数值效果、快速的收敛性质和较完善的局部收敛理论，对其全局收敛性的研究也日趋完善［20－21］。Powell［22］首次证明了采用 Wolfe型非精确线性搜索的BFGS方法关于凸函数的极小化问题是全局收敛的。

检波器组合的方向特性公式为

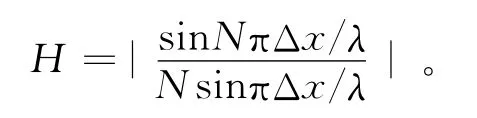
式中：Δx表示检波器组合的组内距；λ表示干扰波的视波长。将分子分母分别用泰勒公式展开并化简得到

取前4项进行计算，写成矩阵的形式为

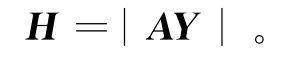
其中：

这样，在向量H已知的情况下，就可以根据BFGS迭代算法反演得到向量Y，最终得到优化后的 ，也就是最佳的组内距。

图11a、b中黑线分别是倾角为20°的斜坡带上12个检波器排列成线性组合和25个检波器排列成面积组合时的特性曲线，组内距为2.000m。以该曲线作为原始输入进行反演优化得到组内距的值分别为1.974m和1.693m，此时的组合特性曲线分别为图11a、b中虚线所示。

通过对比反演优化后的曲线和原始曲线可见，优化后的曲线通放带有向左移动趋势，与原始特性曲线拟合良好，看出反演方法在组合参数设计中的应用是可行的。

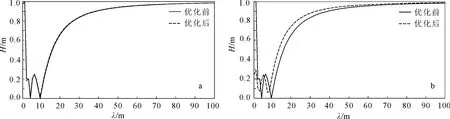
图11 线性组合（a）和面积组合（b）优化后特性曲线Fig.11 Optimized characteristic curve of linear array（a）and area larray（b）

6 结论

1）检波器组合相当于一个低通滤波器，对高频压制较大。在地震勘探野外数据采集中，不同成分的波会受到不同程度的压制，尽管对有效波会有一定压制，但同时也更大程度地压制了干扰波，从提高信噪比的角度看还是值得的。

2）不同的组合图形对组合各个方位传来的干扰压制程度不同，相对于简单的线性组合，面积组合对信噪比的提高更佳；在地表倾斜的地区，大组合基距的图形压制程度较大，且随着倾斜程度的增大，沿上倾方向传来的干扰波压制程度增大，沿下倾方向传来干扰波压制程度减小。

3）检波器组合对视波长较大的干扰响应较大，当有效波与干扰波视波长相差较大时，资料信噪比将会得到很大提高。通过增大检波器组合横向的组合基距可以更好地压制来自垂直排列方向的干扰波，当增大到干扰波的视波长时，响应值最小，对横向干扰压制最大。

4）在实际生产中，检波器组合参数的选取对最终资料的信噪比影响较大，可以利用反演的方法进行检波器组合参数的优化，以求得组合的最佳参数值。

（References）：

［1］张智，李飞，黄志芳，等.地震勘探中检波器组合特性研究［J］.地球物理学进展，2009，24（6）：2117－2121.Zhang Zhi，Li Fei，Huang Zhifang，et al.Study on Character of Geophone Array in Seismic Exploration［J］.Progress in Geophysics，2009，24（6）：2117－2121.

［2］王永刚，段世民，朱兆林，等.复杂地表条件下检波器组合的特性分析［J］.石油地球物理勘探，2003，38（2）：126－130.Wang Yonggang，Duan Shimin，Zhu Zhaolin，et al.Characteristic Analysis of Receiver－Array in Complicated Surface Conditions［J］.Oil Geophysical Prospecting，2003，38（2）：126－130.

［3］卢殿龙，罗春波，袁良信，等.伊通复杂断陷盆地地震采集技术［J］.吉林大学学报：地球科学版，2010，40（增刊）：39－42.Lu Dianlong，Luo Chunbo，Yuan Liangxin，et al.Seismic Acquisition Technology in Yitong Complex Fault Basin［J］.Journal of Jilin University：Earth Science Edition，2010，40（Sup.）：39－42.

［4］Parr J O，Mayne H W.A New Method of Pattern Shooting［J］.Geophysics，1955，20：539－564.

［5］Rigdon H，Hoover G.Quantitative Selection of Seismic Acquisition Parameters［J］.The Leading Edge，1987，6：18－25.

［6］Aldridge D F.Statistically Perturbed Geophone Array Responses［J］.Geophysics，1989，54：1306－1317.

［7］Regone C J.Measurement and Identification of 3－D Coherent Noise Generated from Irregular Surface Carbonates［C］//Palaz I，Marfurt K.Carbonate Seismology.Tulsa：SEG，1997：281－306.

［8］Hoffe B H，Bland C H，Manning M P，et al.Analyzing the Effectiveness of Receiver Arrays for Multicomponent Seismic Exploration［J］.Geophysics，2002，67：1853－1868.

［9］李强.地震勘探检波器组合低频响应问题研究［D］.北京：中国地质大学，2005.Li Qiang.Research on the Problem of Low－Frequency of Geophone Array in Seismic Prospecting［D］.Beijing：China University of Geosciences，2005.

［10］Kerekes K A.Seismic Array Design by Spatial Convolution［J］.Geophysics，2001，66（4）：1195－1207.

［11］田钢，石战结，Xia Jianghai，等.基于自动安置排列的多道面波分析方法［J］.吉林大学学报：地球科学版，2004，34（1）：134－137.Tian Gang，Shi Zhanjie，Xia Jianghai，et al.Multichannel Analysis of Surface Wave Method with the Autojuggie［J］.Journal of Jilin University：Earth Science Edition，2004，34（1）：134－137.

［12］巩向博，吕庆田，韩立国，等.起伏地表地震波场角度域照明分析［J］.吉林大学学报：地球科学版，2013，43（2）：611－615.Gong Xiangbo，Lü Qingtian，Han Liguo，et al.Method of Angle－Domain Illumination Analysis on Rugged Surface［J］.Journal of Jilin University：Earth Science Edition，2013，43（2）：611－615.

［13］熊海金.与面积组合等效的检波器线性组合方法［J］.石油物探，1987，26（3）：80－82.Xiong Haijin.Linear Geophone Array with Nearly the Same Effectiveness of the Areal Ones［J］.Geophysical Prospecting for Petroleum，1987，26（3）：80－82.

［14］Vermeer J O G.三维地震勘探设计［M］.李培明，何永清，译.北京：石油工业出版社，2008.Vermeer J O G.3－D Seismic Survey Design［M］.Translated by Li Peiming，He Yongqing.Beijing：Petroleum Industry Press，2008.

［15］Craig S M，Genter L R.Geophone Array Formation and Semblance Evaluation［J］.Geophysics，2006，71（1）：1－8.

［16］陆基孟.地震勘探原理［M］.东营：石油大学出版社，2001.Lu Jimeng.The Principle of Seismic Exploration［M］.Dongying：China University of Petroleum Press，2011.

［17］石战结.提高灰岩裸露区地震资料信噪比的地震波接收模式研究［R］.杭州：浙江大学，2010.Shi Zhanjie.Study on Seismic Wave Reception Pattern Used to Increase Seismic S/N Ratio in the Limestone Outcrop Areas［R］.Hangzhou：Zhejiang University，2010.

［18］Alhukail A I，Aramco S，Al－Shuhail A A.The Correlation Distance of Incoherent Seismic Noise in Geophone Arrays［J］.SEG，2008：6－10.

［19］李庆忠，魏继东.论检波器横向拉开组合的重要性［J］.石油地球物理勘探，2008，43（4）：375－382.Li Qingzhong，Wei Jidong.Talk About Importance of Cross－Line Array of Geophone on Spread［J］.Oil Geophysical Prospecting，2008，43（4）：375－382.

［20］Dennis J E，More J.A Characterization of Superlinear Convergence and Its Applications to Quasi－Newton Methods［J］.Mathematics of Computation，1974，28：549－560.

［21］Dennis J E，More J.Quasi－Newton Methods，Motivation and Theory［J］.SIAM Review，1977，19：46－89.

［22］Powell M J D.Quadratic Termination Properties of Minimization Algorithm：Part Ⅰand Part Ⅱ［J］.Journal of the Institute of Mathematics and Its Applications，1972，10：333－357.